Этим утром Стефан задал мне сложный вопрос о том, как извлечь коэффициенты из регрессии с категориальными объяснительными переменными. Точнее, он спросил меня, можно ли сохранить коэффициенты в хорошей таблице с информацией о переменной и модальности (эти две информации находятся в двух разных столбцах). Вот некоторый код, который я сделал для создания таблицы, которую он искал, но я предполагаю, что можно использовать некоторые (намного) более умные методы (комментарии — см. Ниже — открыты). Рассмотрим следующий набор данных
> base x sex hair 1 1 H Black 2 4 F Brown 3 6 F Black 4 6 H Black 5 10 H Brown 6 5 H Blonde
с двумя факторами,
> levels(base$hair) [1] "Black" "Blonde" "Brown" > levels(base$sex) [1] "F" "H"
Давайте запустим (стандартную линейную) регрессию,
> reg = lm (x ~ hair + sex, data = base )
который здесь
> summary(reg) Call: lm(formula = x ~ hair + sex, data = base) Residuals: 1 2 3 4 5 6 -3.714e+00 -2.429e+00 2.429e+00 1.286e+00 2.429e+00 -2.220e-16 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.5714 3.4405 1.038 0.408 hairBlonde 0.2857 4.8655 0.059 0.959 hairBrown 2.8571 3.7688 0.758 0.528 sexH 1.1429 3.7688 0.303 0.790 Residual standard error: 4.071 on 2 degrees of freedom Multiple R-squared: 0.2352, Adjusted R-squared: -0.9121 F-statistic: 0.205 on 3 and 2 DF, p-value: 0.886
Если мы хотим извлечь имена факторов (при условии, что здесь нет чисел в имени фактора), и значения связанной модальности, можно использовать
> VARIABLE=c("",gsub("[-^0-9]", "", names(unlist(reg$xlevels)))) > MODALITY=c("",as.character(unlist(reg$xlevels))) > names=data.frame(VARIABLE,MODALITY,NOMVAR=c( + "(Intercept)",paste(VARIABLE,MODALITE,sep="")[-1])) > regression=data.frame(NOMVAR=names(coefficients(reg)), + COEF=as.numeric(coefficients(reg))) > merge(names,regression,all.x=TRUE) NOMVAR VARIABLE MODALITE COEF 1 (Intercept) 3.5714286 2 hairBlack hair Black NA 3 hairBlonde hair Blonde 0.2857143 4 hairBrown hair Brown 2.8571429 5 sexF sex F NA 6 sexH sex H 1.1428571
или, если мы хотим, чтобы формы исключали ссылки,
> merge(names,regression) NOMVAR VARIABLE MODALITE COEF 1 (Intercept) 3.5714286 2 hairBlonde hair Blonde 0.2857143 3 hairBrown hair Brown 2.8571429 4 sexH sex H 1.1428571
Чтобы воспроизвести таблицу, которую мне прислал Стефан, давайте использовать следующий код для создания таблицы HTML:
> library(xtable) > htlmtable <- xtable(merge(names,regression)) > print(htlmtable,type="html")
| NOMVAR | ПЕРЕМЕННЫЕ | МОДАЛЬНОСТЬ | COEF | |
|---|---|---|---|---|
| 1 | (Автоматической переадресации вызова) | 3,57 | ||
| 2 | hairBlonde | волосы | Блондинка | 0,29 |
| 3 | hairBrown | волосы | коричневый | 2,86 |
| 4 | sexH | секс | ЧАС | 1,14 |
Так что да, возможно построить таблицу с переменной, модальностями и коэффициентами. Эта функция может быть интересна для предполагаемой смертности, когда у нас есть большое количество модальностей на фактор (годы, возраст и год рождения). Рассмотрим следующие наборы данных
> DEATH=read.table( + "http://freakonometrics.free.fr/DeathsSwitzerland.txt", + header=TRUE,skip=2) > EXPOSURE=read.table( + "http://freakonometrics.free.fr/ExposuresSwitzerland.txt", + header=TRUE,skip=2) > DEATH$Age=as.numeric(as.character(DEATH$Age)) > DEATH=DEATH[-which(is.na(DEATH$Age)),] > EXPOSURE$Age=as.numeric(as.character(EXPOSURE$Age)) > EXPOSURE=EXPOSURE[-which(is.na(EXPOSURE$Age)),] > base=data.frame(y=as.factor(DEATH$Year),a=as.factor(DEATH$Age), + c=as.factor(DEATH$Year-DEATH$Age),D=DEATH$Total,E= EXPOSURE$Total) > base=base[base$E>0,]
и следующая нелинейная модель, основанная на модели Ли-Картера (включая эффект когорты),
![http://latex.codecogs.com/gif.latex?N_{x,t}\sim\mathcal{P}(E_{x,t}\cdot%20\exp[\alpha_x+\beta_x%20\kappa_t% 20 +% 20 \ gamma_x% 20 \ Delta_ {ТХ}])](/wp-content/uploads/images/dzo/505a027ef1e25dbd7193ee73e01d11e7.latex)
можно оценить, используя
> library(gnm) > reg=gnm(D~a+Mult(a,y)+Mult(a,c),offset=log(E),family=poisson,data=base)
Чтобы извлечь 671 коэффициент из регрессии,
> length(coefficients(reg)) [1] 671
(насколько это возможно), мы должны быть осторожны: имена коэффициентов не так просты в обращении. Например, мы можем видеть такие вещи, как
> coefficients(reg)[200] Mult(., year).age98 0.04203519
Чтобы извлечь их, определите
> na=length((reg$xlevels)$age) > ny=length((reg$xlevels)$year) > nc=length((reg$xlevels)$cohort) > VARIABLElong=c("",rep("age",na),rep("Mult(., year).age",na), + rep("Mult(a, .).y",ny), + rep("Mult(., cohort).age",na),rep("Mult(age, .).cohort",nc)) > VARIABLEshort=c("",rep("age",na),rep("age",na),rep("year",ny), + rep("age",na),rep("cohort",nc)) > MODALITY=c("",(reg$xlevels)$age,(reg$xlevels)$age, + (reg$xlevels)$year,(reg$xlevels)$age,(reg$xlevels)$cohort) > names=data.frame(VARIABLElong,VARIABLEshort, + MODALITY,NOMVAR=c("(Intercept)",paste(VARIABLElong,MODALITY,sep="")[-1])) > regression=data.frame(NOMVAR=names(coefficients(reg)), + COEF=as.numeric(coefficients(reg)))
Здесь мы идем, теперь у нас есть коэффициенты из регрессии в хорошей таблице,
> outputreg=merge(names,regression) > outputreg[1:10,] NOMVAR VARIABLElong VARIABLEshort MODALITY COEF 1 (Intercept) -8.22225458 2 age1 age age 1 -0.87495451 3 age10 age age 10 -1.67145704 4 age100 age age 100 4.91041650 5 age11 age age 11 -1.00186990 6 age12 age age 12 -1.05953497 7 age13 age age 13 -0.90952859 8 age14 age age 14 0.02880668 9 age15 age age 15 0.42830738 10 age16 age age 16 1.35961403
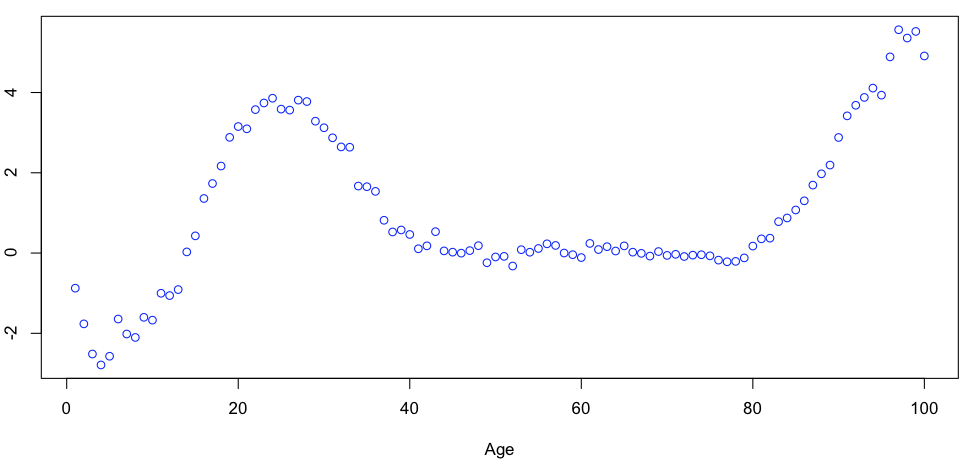
Теперь можно построить все коэффициенты в зависимости от возраста, года наблюдения или года рождения. Например, для стандартного эффекта среднего возраста (а именно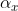 
как функции 
) мы можем использовать
> typevariable=as.character(unique(outputreg$VARIABLElong)) > basegraph=outputreg[outputreg$VARIABLElong==typevariable[2],] > x=as.numeric(as.character(basegraph$MODALITY)) > y=basegraph$COEF > plot(x,y,type="p",col="blue",xlab="Age")
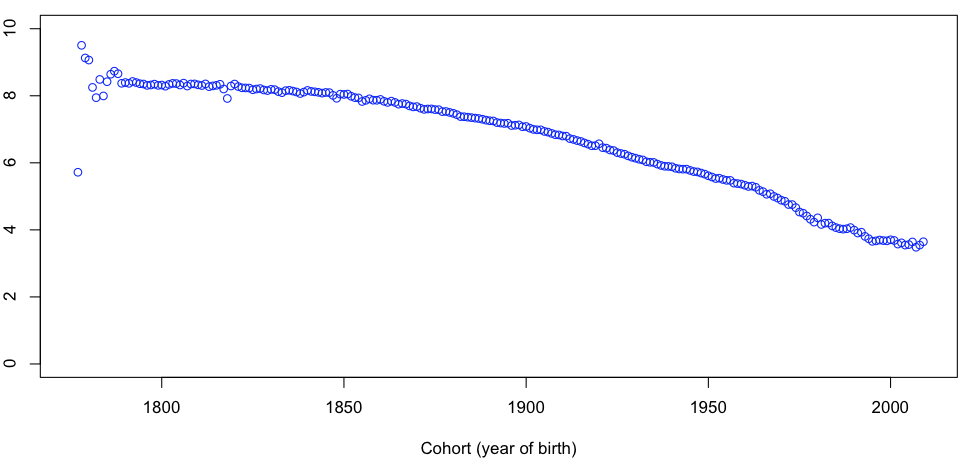
в то время как когортный эффект (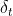 
как функция 
) получается с использованием
> basegraph=outputreg[outputreg$VARIABLElong==typevariable[5],] > x=as.numeric(as.character(basegraph$MODALITY)) > y=basegraph$COEF > plot(x,y,type="p",col="blue",xlab="Cohort (year of birth)",ylim=c(0,10))
