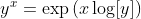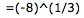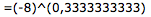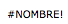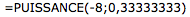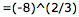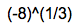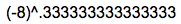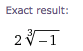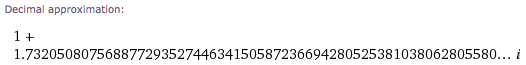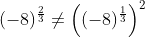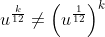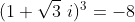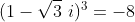Этим утром Матье получил хороший опыт в своем курсе вычислительных методов в актуарной науке . Но давайте начнем с некоторых математических формальных определений.
Во-первых, вспомните, что 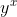
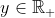
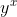
И это определение . Такая функция существует только если 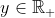
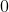
Теперь эта функция «сила» появляется и в комплексном анализе, когда речь идет о единичных корнях. От случая, если 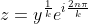
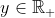
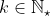
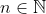
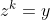
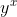
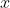
Вернемся к проблеме Матье. На самом деле, в своем курсе, он хотел вычислить 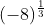
ты получаешь 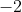
Похоже , эта шляпа функция может быть использована для определения объектов , таких как 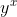
ты получаешь
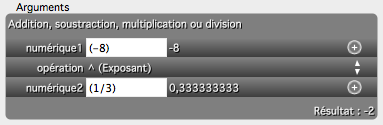
(имеется в виду, что это проблема …). Также можно использовать функцию power ( puissance in French) Excel,
Здесь вы также получите
Странная часть здесь является то, что в окне «помощи», вы можете прочитать , что эта сила функция может быть использована с любым числом в 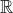
Еще один момент … как насчет 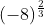
ты получаешь
(аналогично с степенной функцией). Ясно, что не так просто использовать эту функцию мощности. Теперь, если вы используете Google (который теперь является моим новым онлайн-калькулятором, когда я нахожусь в классе, когда я не могу использовать R), если мощность является дробной (или, если быть более точным, обратная величина от целого числа), то она работает как превосходить
ты получаешь
Но если вы печатаете (что должно быть близко, из свойства непрерывности степенной функции)
ты получаешь
и аналогично
В Wolfram Mathworld введите
Mathematica признает, что мы пытаемся иметь дело с единичными корнями: результат здесь
с — как и ожидалось — числовым приближением
С Matlab Матье получил то же самое, что и Mathematica (его десятичное приближение). И в заключение, с R, Матье получил
> (-8)^(1/3) [1] NaN > (-8)^(.333333333333333) [1] NaN
Поэтому для R вы не можете использовать эту функцию с отрицательными числами.
Теперь, как мы можем интерпретировать эти результаты?
1) Я понимаю, что с MS Excel, 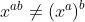
что проблематично. Например, в страховании с ежемесячными скидками у нас есть такие функции, как 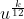
2) Проблема возникает — вероятно (MS Excel не является открытым программным обеспечением, поэтому его может быть трудно проверить) — из-за того факта, что 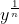
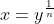
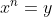
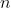
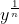
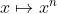
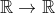
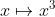
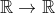
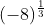
3) Все еще есть проблемы с Google и Mathematica. Это нормально, чтобы вернуть единичные корни в 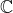
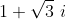
но можно также наблюдать это, и аналогично, 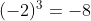
Можно проверить с
С R, так как здесь мы имеем дело не со степенной функцией, а с корнями, если мы хотим найти 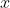
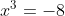
> polyroot(c(8,0,0,1)) [1] 1+1.732051i -2+0.000000i 1-1.732051i
Что отличается … Странно, не правда ли?