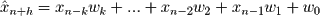Статьи

Прогнозирование потребления пива с помощью Sklearn

Январь 11, 2018

В этом посте мы увидим, как реализовать модель прямого прогнозирования на основе объекта линейной регрессии sklearn. Модель, которую мы собираемся построить, основана на идее идеи, что прошлые наблюдения являются хорошими предикторами будущей ценности. Используя некоторые символы, заданные x n − k , …, x n − 2 , x n − 1, мы хотим оценить x n + h, где h — горизонт прогноза, просто используя заданные значения. Оценка, которую мы собираемся применить, следующая:

где x n − k и x n − 1 — соответственно самое старое и новейшее наблюдение, которое мы рассматриваем для прогноза. Веса w k , …, w 1 , w 0 выбираются для минимизации

где m — количество периодов, доступных для обучения нашей модели. Эту модель часто называют регрессионной моделью с запаздывающими объясняющими переменными, а k называется запаздывающим порядком.

Перед внедрением модели загрузим временной ряд для прогноза: 

import pandas as pd
df = pd.read_csv('NZAlcoholConsumption.csv')
to_forecast = df.TotalBeer.values
dates = df.DATE.values

Временные ряды представляют общее количество алкоголя, потребленного на четверть миллиона литров с 1-го квартала 2000 года по 3-й квартал 2012 года. Данные предоставлены правительством Новой Зеландии и могут быть загружены в формате CSV отсюда . Мы сосредоточимся на прогнозе потребления пива.

Во-первых, нам нужно организовать наши данные в прогнозе в окнах, которые содержат предыдущие наблюдения: 

import numpy as np

def organize_data(to_forecast, window, horizon):"""
     Input:
      to_forecast, univariate time series organized as numpy array
      window, number of items to use in the forecast window
      horizon, horizon of the forecast
     Output:
      X, a matrix where each row contains a forecast window
      y, the target values for each row of X
    """
    shape = to_forecast.shape[:-1]+/(to_forecast.shape[-1]- window +1, window)
    strides = to_forecast.strides +(to_forecast.strides[-1],)
    X = np.lib.stride_tricks.as_strided(to_forecast, 
                                        shape=shape, 
                                        strides=strides)
    y = np.array([X[i+horizon][-1]for i in range(len(X)-horizon)])return X[:-horizon], y

k =4# number of previous observations to use
h =1# forecast horizon
X,y = organize_data(to_forecast, k, h)

Теперь X — это матрица, в которой i-я строка содержит отстающие переменные x n-k , …, x n-2 , x n-1, а y [i] содержит i-е целевое значение. Мы готовы обучить нашу модель прогнозирования:

from sklearn.linear_model importLinearRegression
 
m =10# number of samples to take in account
regressor =LinearRegression(normalize=True)
regressor.fit(X[:m], y[:m])

Мы обучили нашу модель, используя первые 10 наблюдений, что означает, что мы использовали данные с 1-го квартала 2000 года до 2-го квартала 2002 года. Мы используем порядок отставания в один год и прогнозируемый горизонт 1 квартал. Для оценки ошибки модели мы будем использовать среднюю абсолютную процентную ошибку (MAPE). Вычисляя эту метрику для сравнения прогноза оставшегося наблюдения временного ряда и фактических наблюдений, мы имеем:

def mape(ypred, ytrue):""" returns the mean absolute percentage error """
    idx = ytrue !=0.0return100*np.mean(np.abs(ypred[idx]-ytrue[idx])/ytrue[idx])print'The error is %0.2f%%'% mape(regressor.predict(X[m:]),y[m:])
The error is 6.15%

Это означает, что в среднем прогноз, предоставляемый нашей моделью, отличается от целевого значения только на 6,15%. Давайте сравним прогноз и наблюдаемые значения визуально:

figure(figsize=(8,6))
plot(y, label='True demand', color='#377EB8', linewidth=2)
plot(regressor.predict(X),'--', color='#EB3737', linewidth=3, label='Prediction')
plot(y[:m], label='Train data', color='#3700B8', linewidth=2)
xticks(arange(len(dates))[1::4],dates[1::4], rotation=45)
legend(loc='upper right')
ylabel('beer consumed (millions of litres)')
show()

Мы отмечаем, что прогноз очень близок к целевым значениям и что модель смогла узнать тенденции и предвидеть их во многих случаях.

35
Share: