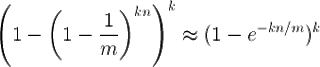Фильтр Блума — это структура данных, разработанная для быстрого и эффективного использования памяти, присутствует ли элемент в наборе. Он основан на вероятностном механизме, при котором возможны ложноположительные результаты поиска, а ложноотрицательные — нет. В этом посте мы увидим чистую реализацию фильтра Блума на python, а в конце мы увидим, как настроить параметры, чтобы минимизировать количество ложноположительных результатов.
Давайте начнем с небольшой теории. Идея фильтра состоит в том, чтобы выделить битовый вектор длиной m , изначально все равным 0, а затем выбрать k независимых хеш-функций, h 1 , h 2 , …, h k , каждая из которых имеет диапазон [ 1 м ]. Когда элемент a добавляется в набор, то биты в позициях h (a) 1 , h (a) 2 , …, h (a) k в битовом векторе устанавливаются на 1. Для элемента запроса q мы может проверить, находится ли он в наборе, используя биты в позициях h (a) 1 , h (a) 2 , …, h (a) k в векторе. Если любой из этих битов равен 0, мы сообщаем, что q нет в наборе, в противном случае мы сообщаем, что q есть. Мы должны заботиться о том, чтобы в первом случае оставалась некоторая вероятность того, что q не входит в набор, что может привести к ложному положительному ответу.
Следующий класс является наивной реализацией фильтра Блума (обратите внимание: эта реализация не должна подходить для производства. Она сделана просто для того, чтобы показать, как работает фильтр Блума и изучить его поведение):
classBloom:""" Bloom Filter """def __init__(self,m,k,hash_fun):"""
m, size of the vector
k, number of hash fnctions to compute
hash_fun, hash function to use
"""self.m = m
self.vector =[0]*m # initialize the vectorself.k = k
self.hash_fun = hash_fun
self.data ={}# data structure to store the dataself.false_positive =0def insert(self,key,value):""" insert the pair (key,value) in the database """self.data[key]= value
for i in range(self.k):self.vector[self.hash_fun(key+str(i))%self.m]=1def contains(self,key):""" check if key is cointained in the database
using the filter mechanism """for i in range(self.k):ifself.vector[self.hash_fun(key+str(i))%self.m]==0:returnFalse# the key doesn't existreturnTrue# the key can be in the data setdefget(self,key):""" return the value associated with key """ifself.contains(key):try:returnself.data[key]# actual lookupexceptKeyError:self.false_positive +=1
Использовать этот фильтр довольно просто, мы должны инициализировать структуру данных с помощью хеш-функции, значения для
k и размера битового вектора, после чего мы можем начать добавлять элементы, как в этом примере:
import hashlib
def hash_f(x):
h = hashlib.sha256(x)returnint(h.hexdigest(),base=16)
b =Bloom(100,10,hash_f)
b.insert('this is a key','this is a value')print b.get('this is a key')
Теперь проблема состоит в том, чтобы выбрать параметры фильтра, чтобы минимизировать количество ложноположительных результатов. Мы имеем, что после вставки
n элементов в таблицу размера
m вероятность того, что конкретный бит по-прежнему равен 0, равна
Следовательно, после
n вставок вероятность того, что определенный бит равен 1, равна
Таким образом, для фиксированных параметров
m и
n оптимальное значение
k , минимизирующее эту вероятность, равно
Имея это в виду, мы можем проверить наш фильтр. Первое, что нам нужно, это функция, которая проверяет фильтр Блума на фиксированные значения
m ,
n и
k, подсчитывая процент ложных срабатываний:
import random def rand_data(n, chars):""" generate random strings using the characters in chars """return''.join(random.choice(chars)for i in range(n))def bloomTest(m,n,k):""" return the percentage of false positive """ bloom =Bloom(m,k,hash_f)# generating a random data rand_keys =[rand_data(10,'abcde')for i in range(n)]# pushing the items into the data structurefor rk in rand_keys: bloom.insert(rk,'data')# adding other elements to the dataset rand_keys = rand_keys +[rand_data(10,'fghil')for i in range(n)]# performing a query for each element of the datasetfor rk in rand_keys: bloom.get(rk)returnfloat(bloom.false_positive)/n*100.0
Если мы зафиксируем
m = 10000 и
n = 1000, согласно приведенным выше уравнениям, мы получим, что значение
k, которое минимизирует число ложных срабатываний, составляет около 6,9314. Мы можем подтвердить это экспериментально с помощью следующего теста:
# testing the filter
m =10000
n =1000
k = range(1,64)
perc =[bloomTest(m,n,kk)for kk in k]# k is varying# plotting the result of the testfrom pylab import plot,show,xlabel,ylabel
plot(k,perc,'--ob',alpha=.7)
ylabel('false positive %')
xlabel('k')
show()
Результат теста должен быть следующим
Глядя на график, мы можем подтвердить, что для k около 7 у нас самый низкий процент ложных срабатываний.