После моего предыдущего поста , еще несколько вещей. Как уже упоминал Фредерик, действительно возможно вычислить вероятность всех пар. Точнее, все пары встречаются не так часто: некоторые команды могут играть против (почти) всех, а другие — нет. Из предыдущей таблицы можно вычислить вероятность того, что последняя команда сыграет против команды 1. Или команды 2 (числа взяты из файла xls, упомянутого ранее). Чтобы сделать это просто
> table(M[,2*n])/length(M[,2*n])*100 1 2 3 5 7 10 11 11.82500 12.61212 12.61212 13.25279 19.31173 18.70767 11.67856
Здесь последняя команда (как я их оценил) имеет 11,8% шансов сыграть против команды 1 и 19,3% — против команды 7. Если мы вычислим все вероятности, мы получим
> S
1 2 3 5 7 10 11 13
4 0.00 14.16 14.16 0.00 22.22 21.25 13.05 15.13
6 12.52 13.19 13.19 14.11 20.13 0.00 12.35 14.47
8 18.78 0.00 19.54 21.50 0.00 0.00 18.39 21.76
9 18.78 19.54 0.00 21.50 0.00 0.00 18.39 21.76
12 14.68 15.54 15.54 16.56 0.00 23.19 14.47 0.00
14 11.64 12.37 12.37 13.05 18.96 18.25 0.00 13.34
15 11.77 12.55 12.55 0.00 19.36 18.59 11.64 13.50
16 11.82 12.61 12.61 13.25 19.31 18.70 11.67 0.00
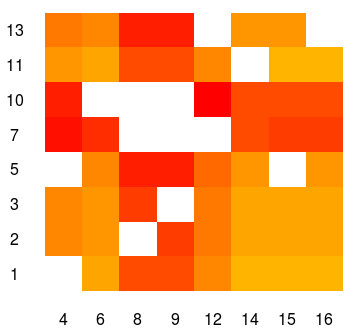
это можно увидеть ниже
Белые области не могут быть достигнуты, в то время как красные более вероятны. Здесь мы вычисляем вероятность того, что домашняя команда (указанная на оси X ) сыграет с какой-либо командой посетителей (на оси Y ). Тот факт, что эти вероятности не являются равномерными, кажется странным. Но я думаю, что это происходит из-за этих ограничений …
Еще один странный момент: зайти в тупик. По крайней мере, с техникой, которую я использовал. До сих пор я их не считал. Но мы можем, просто следующий код
> U=c(4,6,8,9,12,14,15,16) > a1=U[1] > b1=U[2] > c1=U[3] > d1=U[4] > e1=U[5] > f1=U[6] > g1=U[7] > h1=U[8] > a2=b2=c2=d2=e2=f2=g2=h2=NA > posa2=(1:n)%notin%c(LISTEIMPOSSIBLE[,a1]) > if(length(posa2)==0){na=na+1} > for(a2 in posa2){ + posb2=(1:n)%notin%c(LISTEIMPOSSIBLE[,b1],a2) + if(length(posb2)==0){na=na+1} + for(b2 in posb2){ + posc2=(1:n)%notin%c(LISTEIMPOSSIBLE[,c1],a2,b2) + if(length(posc2)==0){na=na+1} + for(c2 in posc2){ + posd2=(1:n)%notin%c(LISTEIMPOSSIBLE[,d1], + a2,b2,c2) + if(length(posd2)==0){na=na+1} + for(d2 in posd2){ + pose2=(1:n)%notin%c(LISTEIMPOSSIBLE[,e1], + a2,b2,c2,d2) + if(length(pose2)==0){na=na+1} + for(e2 in pose2){ + posf2=(1:n)%notin%c(LISTEIMPOSSIBLE[,f1], + a2,b2,c2,d2,e2) + if(length(posf2)==0){na=na+1} + for(f2 in posf2){ + posg2=(1:n)%notin%c(LISTEIMPOSSIBLE[,g1], + a2,b2,c2,d2,e2,f2) + if(length(posg2)==0){na=na+1} + for(g2 in posg2){ + posh2=(1:n)%notin%c(LISTEIMPOSSIBLE[,h1], + a2,b2,c2,d2,e2,f2,g2) + if(length(posh2)==0){na=na+1} + for(h2 in posh2){ + s=s+1 + V=c(a1,a2,b1,b2,c1,c2,d1,d2,e1,e2,f1,f2,g1,g2,h1,h2) + }}}}}}}}
При первоначальном заказе команды хозяев количество тупиков было
> na [1] 657
Вероятность получения тупика тогда
> 657/(657+5463) [1] 0.1073529
(657 сценариев закончились тупиком, а 5463 — хорошо). Худший случай был получен, когда мы рассмотрели
[1] 6 4 16 14 12 15 8 9
В этом случае вероятность получения тупика была
> 4047/(4047+5463) [1] 0.4255521
Здесь это явно зависит от порядка. Так что если мы рисуем — случайным образом — порядок хозяев, то есть
> Urandom=sample(U,size=8)
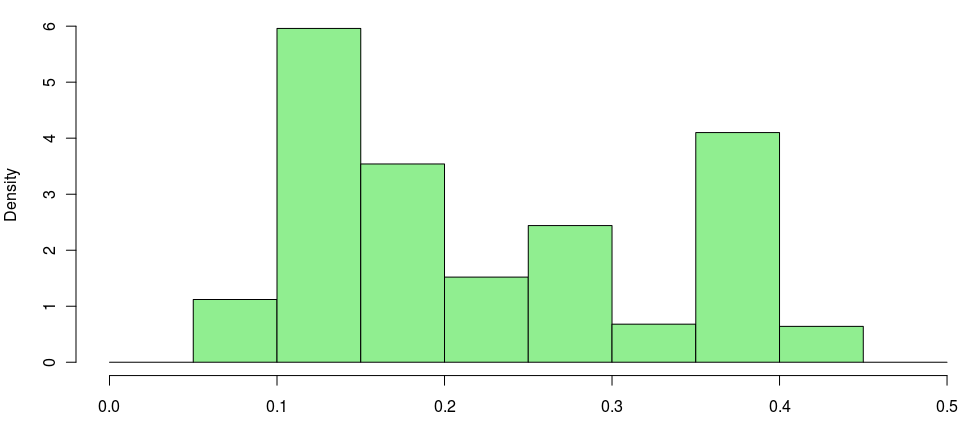
Распределение вероятности возникновения тупика
Все эти вычисления были основаны на моем понимании рисунков. Но Кристоф (aka @ ciebiera ) в своем блоге krzysztofciebiera.blogspot.ca/… получил разные результаты. Например, исходя из моих предыдущих расчетов , вероятность получить идентичные пары составляла 0,018349% (1 шанс из 5463), но Кристоф получил — основываясь на процедуре УЕФА (как он это назвал) — вероятность 0,0181337%. Что не является строго одним и тем же, но оба вычисления дают относительно близкие результаты …