Оптимизация — очень распространенная проблема в анализе данных. Учитывая набор переменных (которые контролируют), как правильно выбрать значение, чтобы выгода была максимальной. Более формально, оптимизация заключается в определении набора переменных x1, x2,…, которые максимизируют или минимизируют целевую функцию f (x1, x2,…).
Неограниченная оптимизация
В случае без ограничений переменная может быть свободно выбрана в пределах ее полного диапазона.
Типичным решением является вычисление вектора градиента целевой функции [∂f / ∂x1, ∂f / ∂x2,…] и установка его в [0, 0,…]. Решите это уравнение и выведите результат x1, x2…, который даст локальный максимум.
В R это можно сделать методом численного анализа.
> f <- function(x){(x[1] - 5)^2 + (x[2] - 6)^2}
> initial_x <- c(10, 11)
> x_optimal <- optim(initial_x, f, method="CG")
> x_min <- x_optimal$par
> x_min
[1] 5 6
Оптимизация ограничений равенства
Переходя к ограниченному случаю, скажем, x1, x2… не являются независимыми, а затем должны быть связаны друг с другом определенным образом: g1 (x1, x2,…) = 0, g2 (x1, x2,…) = 0.
Задача оптимизации может быть выражена как…
Максимизировать целевую функцию:
f (x1, x2,…) С
учетом ограничений равенства:
- g1 (x1, x2,…) = 0
- g2 (x1, x2,…) = 0
Типичное решение — превратить проблему оптимизации ограничений в задачу оптимизации без ограничений с использованием множителей Лагранжа.
Определите новую функцию F следующим образом …
F (x1, x2,…, λ1, λ2,…) = f (x1, x2,…) + λ1.g1 (x1, x2,…) + λ2.g2 (x1 , x2,…) +…
Тогда решите для …
[∂F / ∂x1, ∂F / ∂x2,…, ∂F / ∂λ1, ∂F / ∂λ2,…] = [0, 0,…. ]
Оптимизация ограничения неравенства
В этом случае ограничение является неравенством. Мы не можем использовать метод множителей Лагранжа, потому что он требует ограничения равенства. Не существует общего решения для произвольных ограничений неравенства.
Тем не менее, мы можем поставить некоторые ограничения в виде ограничения. Далее мы изучаем две модели, в которых ограничение ограничено линейной функцией переменных:
w1.x1 + w2.x2 +…> = 0
Линейное программирование
Линейное программирование — это модель, в которой и целевая функция, и функция ограничения ограничены как линейная комбинация переменных. Задача линейного программирования может быть определена следующим образом …
Максимизировать целевую функцию:
f (x1, x2) = c1.x1 + c2.x2 С учетом
ограничений неравенства:
- a11.x1 + a12.x2 <= b1
- a21.x1 + a22.x2 <= b2
- a31.x1 + a32.x2 <= b3
- x1> = 0, x2> = 0
В качестве наглядного примера рассмотрим проблему портфельных инвестиций. В этом примере мы хотим найти оптимальный способ распределения доли активов в нашем инвестиционном портфеле.
- StockA дает в среднем 5% прибыли
- StockB дает в среднем 4% прибыли
- StockC дает в среднем 6% прибыли
Чтобы установить некоторые ограничения, допустим, что мои инвестиции в C должны быть меньше суммы A, B. Кроме того, инвестиции в A не могут быть более чем вдвое больше B. Наконец, по крайней мере, 10% инвестиций в каждую акцию.
Чтобы сформулировать эту проблему:
Переменная: x1 =% инвестиций в A, x2 =% в B, x3 =% в C
Максимальная ожидаемая доходность:
f (x1, x2, x3) = x1 * 5% + x2 * 4% + x3 * 6% С
учетом ограничений:
- 10% <x1, x2, x3 <100%
- х1 + х2 + х3 = 1
- х3 <х1 + х2
- х1 <2 * х2
> library(lpSolve) > library(lpSolveAPI) > # Set the number of vars > model <- make.lp(0, 3) > # Define the object function: for Minimize, use -ve > set.objfn(model, c(-0.05, -0.04, -0.06)) > # Add the constraints > add.constraint(model, c(1, 1, 1), "=", 1) > add.constraint(model, c(1, 1, -1), ">", 0) > add.constraint(model, c(1, -2, 0), "<", 0) > # Set the upper and lower bounds > set.bounds(model, lower=c(0.1, 0.1, 0.1), upper=c(1, 1, 1)) > # Compute the optimized model > solve(model) [1] 0 > # Get the value of the optimized parameters > get.variables(model) [1] 0.3333333 0.1666667 0.5000000 > # Get the value of the objective function > get.objective(model) [1] -0.05333333 > # Get the value of the constraint > get.constraints(model) [1] 1 0 0
Квадратичное программирование
Квадратичное программирование — это модель, в которой целевая функция представляет собой квадратичную функцию (содержит до двух слагаемых), а функция ограничения ограничена как линейная комбинация переменных.
Задача квадратичного программирования может быть определена следующим образом …
Минимизировать квадратичную целевую функцию:
f (x1, x2) = c1.x12 + c2. x1x2 + c2.x22 — (d1. x1 + d2.x2)
С учетом ограничений
- a11.x1 + a12.x2 == b1
- a21.x1 + a22.x2 == b2
- a31.x1 + a32.x2> = b3
- a41.x1 + a42.x2> = b4
- a51.x1 + a52.x2> = b5
Выразите проблему в матричной форме:
Минимизируйте цель
½ (DTx) — dTx
С учетом ограничения
ATx> = b
Первые k столбцов A — это ограничение равенства.
В качестве иллюстративного примера давайте продолжим рассмотрение проблемы портфельных инвестиций. В этом примере мы хотим найти оптимальный способ распределения доли активов в нашем инвестиционном портфеле.
- StockA дает в среднем 5% прибыли
- StockB дает в среднем 4% прибыли
- StockC дает в среднем 6% прибыли
Мы также изучаем дисперсию каждой акции (известную как риск), а также ковариацию между акциями.
Что касается инвестиций, мы хотим не только получить высокую ожидаемую прибыль, но и низкую дисперсию. Другими словами, акции с высокой доходностью, но и с высокой дисперсией не очень привлекательны. Поэтому максимизация ожидаемой доходности и минимизация отклонений является типичной инвестиционной стратегией.
Один из способов минимизировать дисперсию — это выбрать несколько акций (в портфеле) для диверсификации инвестиций. Диверсификация происходит, когда компоненты акций в портфеле движутся от их среднего значения в другом направлении (следовательно, дисперсия уменьшается).
Ковариационная матрица ∑ (между каждой парой акций) представлена следующим образом:
1%, 0,2%, 0,5%,
0,2%, 0,8%, 0,6%.
0,5%, 0,6%, 1,2%
В этом примере мы хотим добиться общей доходности не менее 5,2% при минимальной дисперсии доходности.
Для формулирования проблемы:
Переменная: x1 =% инвестиций в A, x2 =% в B, x3 =% в C.
Свести к минимуму дисперсию:
xT∑x Подлежит
ограничению:
- х1 + х2 + х3 == 1
- X1 * 5% + x2 * 4% + x3 * 6%> = 5,2%
- 0% <x1, x2, x3 <100%
> library(quadprog) > mu_return_vector <- c(0.05, 0.04, 0.06) > sigma <- matrix(c(0.01, 0.002, 0.005, + 0.002, 0.008, 0.006, + 0.005, 0.006, 0.012), + nrow=3, ncol=3) > D.Matrix <- 2*sigma > d.Vector <- rep(0, 3) > A.Equality <- matrix(c(1,1,1), ncol=1) > A.Matrix <- cbind(A.Equality, mu_return_vector, diag(3)) > b.Vector <- c(1, 0.052, rep(0, 3)) > out <- solve.QP(Dmat=D.Matrix, dvec=d.Vector, Amat=A.Matrix, bvec=b.Vector, meq=1) > out$solution [1] 0.4 0.2 0.4 > out$value [1] 0.00672 >
Интеграция с прогнозной аналитикой
Оптимизация обычно интегрируется с прогнозной аналитикой, которая является еще одной важной частью аналитики данных. Для обзора
прогнозной аналитики , вот
мой предыдущий блог об этом.
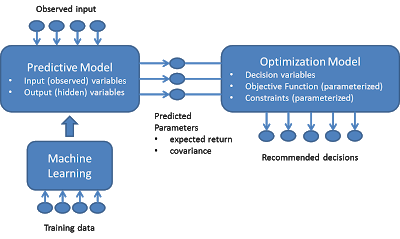
Общая обработка может быть изображена следующим образом:
На этой диаграмме мы используем машинное обучение для обучения модели прогнозирования в пакетном режиме. Как только прогнозная модель становится доступной, в нее в реальном времени поступают данные наблюдений и прогнозируется набор выходных переменных. Такая выходная переменная будет введена в модель оптимизации в качестве параметров среды (например, доходность каждого запаса, ковариация и т. Д.), Из которых рекомендуется набор оптимальных переменных решения.