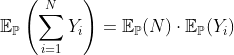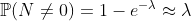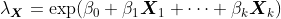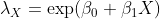Статьи

Natura Non Facit Saltus

Октябрь 23, 2018

(см. статью Джона Уилкинса об интересной истории этой фразы  http://scienceblogs.com/evolvingoughtts/… ). Мы увидим несколько методов сглаживания для страхования ставок. Для начала предположим, что мы не хотим использовать методы сегментации: все будут платить одинаковую цену.

  • нет сегментации премии

И эта цена должна быть связана с чистой премией, которая пропорциональна частоте (или годовой частоте, как обсуждалось  ранее ), так как

http://latex.codecogs.com/gif.latex?\mathbb{E}_{\mathbb{P}}\left(\sum_{i=1}^N%20Y_i\right)=\mathbb{E} _ {\ mathbb {P}} (N),% 20 \ CDOT% 20 \ mathbb {E} _ {\ mathbb {P}} (Y_i)

Мера вероятности упоминается здесь просто чтобы напомнить, что мы можем использовать любую меру. Четный 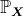 http://latex.codecogs.com/gif.latex?\mathbb{P}_{\boldsymbol{X}} (на основе некоторых ковариат). Без какого-либо ковариата ожидаемая частота должна быть

> regglm0=glm(nbre~1+offset(log(exposition)),data=sinistres,family=poisson)
> summary(regglm0)

Call:
glm(formula = nbre ~ 1 + offset(log(exposition)), family = poisson, 
    data = sinistres)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-0.5033  -0.3719  -0.2588  -0.1376  13.2700  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -2.6201     0.0228  -114.9   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 12680  on 49999  degrees of freedom
Residual deviance: 12680  on 49999  degrees of freedom
AIC: 16353

Number of Fisher Scoring iterations: 6
> exp(coefficients(regglm0))
(Intercept) 
 0.07279295

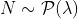
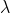
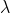
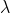
Таким образом, если мы не хотим принимать во внимание потенциальную неоднородность, мы должны предположить, что  http://latex.codecogs.com/gif.latex?N\sim\mathcal{P}(\lambda)где  http://latex.codecogs.com/gif.latex?\lambda закрыто до 7,28%. Да, как уже упоминалось в классе, это довольно часто, чтобы увидеть  http://latex.codecogs.com/gif.latex?\lambda в процентах, то есть вероятность, так как

http://latex.codecogs.com/gif.latex?\mathbb{P}(N\neq%200)=1-e^{-\lambda}\approx%20\lambda

т. е.  http://latex.codecogs.com/gif.latex?\lambda может быть истолковано как вероятность не иметь требования (см. также  закон малых чисел ). Давайте представим это в зависимости от возраста водителя,

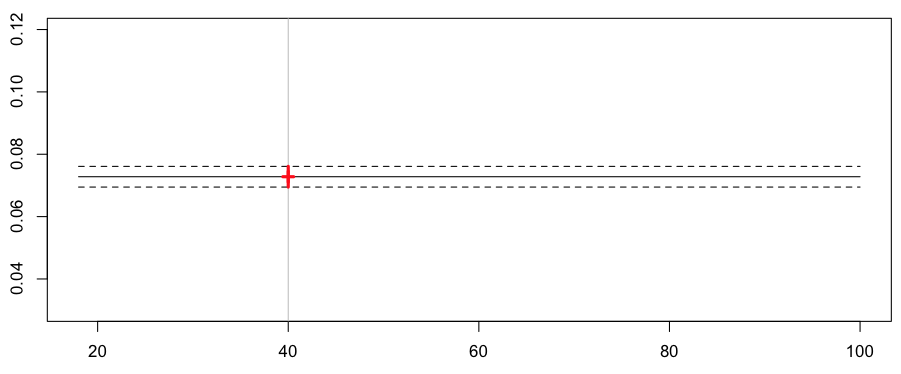
> a=18:100
> yp=predict(regglm0,newdata=data.frame(ageconducteur=a,exposition=1),type="response",se.fit=TRUE)
> yp0=yp$fit
> yp1=yp$fit+2*yp$se.fit
> yp2=yp$fit-2*yp$se.fit
> plot(a,yp0,type="l",ylim=c(.03,.12))
> abline(v=40,col="grey")
> lines(a,yp1,lty=2)
> lines(a,yp2,lty=2)
> k=23
> points(a[k],yp0[k],pch=3,lwd=3,col="red")
> segments(a[k],yp1[k],a[k],yp2[k],col="red",lwd=3)

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-constante.png

Мы прогнозируем одинаковую частоту для всех драйверов, например, для некоторых дисков в возрасте 40 лет,

> cat("Frequency =",yp0[k]," confidence interval",yp1[k],yp2[k])
Frequency = 0.07279295  confidence interval 0.07611196 0.06947393

Давайте теперь рассмотрим случай, когда мы пытаемся учитывать неоднородность, например, по возрасту,

  • (Стандартная) пуассоновская регрессия

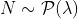
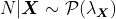
Идея (логарифмически) регрессии Пуассона заключается в предположении , что вместо того  http://latex.codecogs.com/gif.latex?N\sim\mathcal{P}(\lambda), мы должны иметь  http://latex.codecogs.com/gif.latex?N|\boldsymbol{X}\sim\mathcal{P}(\lambda_{\boldsymbol{X}}), где

http://latex.codecogs.com/gif.latex?\lambda_{\boldsymbol{X}}=\exp(\beta_0+\beta_1%20\boldsymbol{X}_1+\cdots+\beta_k\boldsymbol{X}_k)

в очень общей обстановке. Здесь рассмотрим только одну объясняющую переменную, т.е.

http://latex.codecogs.com/gif.latex?\lambda_{X}=\exp(\beta_0+\beta_1%20{X})

Здесь мы имеем

> yp=predict(regglm1,newdata=data.frame(ageconducteur=a,exposition=1),
+ type="response",se.fit=TRUE)
> yp0=yp$fit
> yp1=yp$fit+2*yp$se.fit
> yp2=yp$fit-2*yp$se.fit
> plot(a,yp0,type="l",ylim=c(.03,.12))
> abline(v=40,col="grey")
> lines(a,yp1,lty=2)
> lines(a,yp2,lty=2)
> points(a[k],yp0[k],pch=3,lwd=3,col="red")
> segments(a[k],yp1[k],a[k],yp2[k],col="red",lwd=3)

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-exp-standard.png

т. е. прогноз по частоте ежегодных претензий для нашего 40-летнего водителя сейчас составляет 7,74% (что немного выше, чем у нас было раньше, 7,28%)

> cat("Frequency =",yp0[k]," confidence interval",yp1[k],yp2[k])
Frequency = 0.07740574  confidence interval 0.08117512 0.07363636

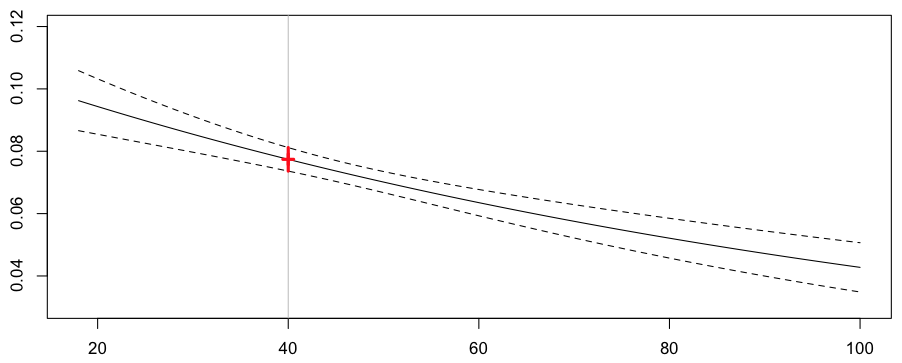
Можно рассчитать не ожидаемую частоту, а соотношение 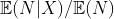 http://latex.codecogs.com/gif.latex?\mathbb{E}(N|X)/\mathbb{E}(N).

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/Capture-d%E2%80%99e%CC%81cran-2013-02-05-a%CC% 80-13.45.43.png

Выше горизонтальной синей линии премия будет выше, чем полученная без сегментации, и (конечно) ниже ниже. Здесь водители младше 44 лет будут платить больше, а водители старше 44 лет — меньше. Мы обсуждали во введении необходимость сегментации. Если мы рассмотрим две компании, одна из которых сегментируется, а другая имеет фиксированную ставку, то более старые водители перейдут в первую компанию (поскольку страхование дешевле), а более молодые — во вторую (опять же, дешевле). Проблема в том, что вторая компания неявно надеется, что пожилые водители возместят риск. Но так как они ушли, страхование будет слишком дешевым, и компания потеряет деньги (если не обанкротится). Поэтому компании должны использовать методы сегментации, чтобы выжить. Теперь,проблема в том, что мы не можем быть уверены, что это экспоненциальное снижение премии является правильным способом, которым премия должна эволюционировать как функция возраста. Альтернативой может быть использование непараметрических методов для визуализации истинное  влияние возраста на частоту претензий.

  • Чистая непараметрическая модель

Первой моделью можно считать премию за возраст. Это может быть сделано с учетом возраста водителя как фактора  регрессии,

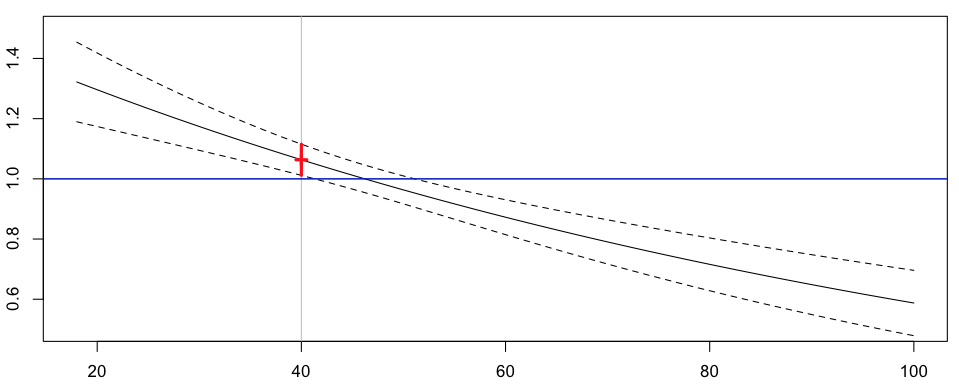
> regglm2=glm(nbre~as.factor(ageconducteur)+offset(log(exposition)),
+ data=sinistres,family=poisson)
> yp=predict(regglm2,newdata=data.frame(ageconducteur=a0,exposition=1),
+ type="response",se.fit=TRUE)
> yp0=yp$fit
> yp1=yp$fit+2*yp$se.fit
> yp2=yp$fit-2*yp$se.fit
> plot(a0,yp0,type="l",ylim=c(.03,.12))
> abline(v=40,col="grey")

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-factors.png

Здесь прогноз для нашего 40-летнего водителя немного ниже, чем предыдущий, но доверительный интервал намного больше (поскольку мы ориентируемся на очень маленький подкласс портфеля: водители в возрасте  ровно  40)

Frequency = 0.06686658  confidence interval 0.08750205 0.0462311

Здесь мы рассматриваем слишком маленькие классы, и премия слишком неустойчива: премия снизится на 20% с 40 до 41 года, а затем увеличится на 50% с 41 до 42 лет,

> diff(log(yp0[23:25]))
        24         25 
-0.2330241  0.5223478

Нет шансов, что компания будет застрахована с этой стратегией. Это  прерывание  премии явно является важной проблемой здесь.

  • Использование возрастных классов

Альтернативой может быть рассмотрение возрастных классов, от очень молодых водителей до старших водителей.

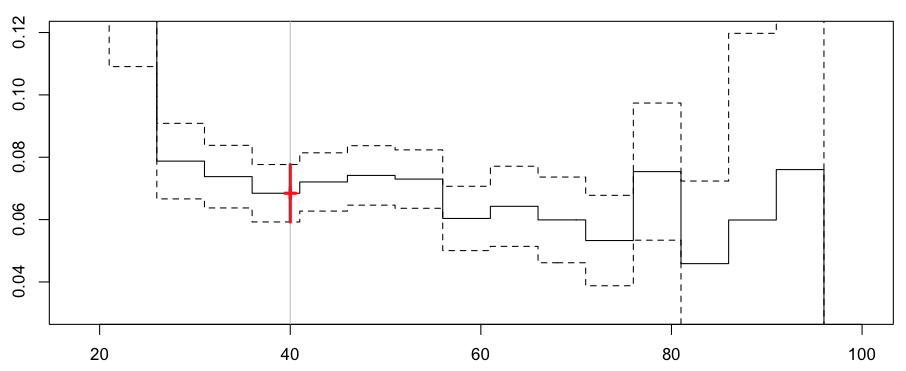
> level1=seq(15,105,by=5)
> regglmc1=glm(nbre~cut(ageconducteur,level1)+offset(log(exposition)),
+ data=sinistres,family=poisson)
> summary(regglmc1)

Coefficients:
                                   Estimate Std. Error z value Pr(>|z|)    
(Intercept)                         -1.6036     0.1741  -9.212  < 2e-16 ***
cut(ageconducteur, level1)(20,25]   -0.4200     0.1948  -2.157   0.0310 *  
cut(ageconducteur, level1)(25,30]   -0.9378     0.1903  -4.927 8.33e-07 ***
cut(ageconducteur, level1)(30,35]   -1.0030     0.1869  -5.367 8.02e-08 ***
cut(ageconducteur, level1)(35,40]   -1.0779     0.1866  -5.776 7.65e-09 ***
cut(ageconducteur, level1)(40,45]   -1.0264     0.1858  -5.526 3.28e-08 ***
cut(ageconducteur, level1)(45,50]   -0.9978     0.1856  -5.377 7.58e-08 ***
cut(ageconducteur, level1)(50,55]   -1.0137     0.1855  -5.464 4.65e-08 ***
cut(ageconducteur, level1)(55,60]   -1.2036     0.1939  -6.207 5.40e-10 ***
cut(ageconducteur, level1)(60,65]   -1.1411     0.2008  -5.684 1.31e-08 ***
cut(ageconducteur, level1)(65,70]   -1.2114     0.2085  -5.811 6.22e-09 ***
cut(ageconducteur, level1)(70,75]   -1.3285     0.2210  -6.012 1.83e-09 ***
cut(ageconducteur, level1)(75,80]   -0.9814     0.2271  -4.321 1.55e-05 ***
cut(ageconducteur, level1)(80,85]   -1.4782     0.3371  -4.385 1.16e-05 ***
cut(ageconducteur, level1)(85,90]   -1.2120     0.5294  -2.289   0.0221 *  
cut(ageconducteur, level1)(90,95]   -0.9728     1.0150  -0.958   0.3379    
cut(ageconducteur, level1)(95,100] -11.4694   144.2817  -0.079   0.9366    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

> yp=predict(regglmc1,newdata=data.frame(ageconducteur=a,exposition=1),
+ type="response",se.fit=TRUE)
> yp0=yp$fit
> yp1=yp$fit+2*yp$se.fit
> yp2=yp$fit-2*yp$se.fit
> plot(a,yp0,ylim=c(.03,.12),type="s")
> abline(v=40,col="grey")
> lines(a,yp1,lty=2,type="s")
> lines(a,yp2,lty=2,type="s")

Здесь мы получаем следующие предсказания,

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-cut-1.png

и для нашего 40-летнего водителя частота теперь составляет 6,84%.

Frequency = 0.0684573  confidence interval 0.07766717 0.05924742

Но наши классы были определены здесь произвольно. Возможно, мы должны рассмотреть другие классы, чтобы увидеть, чувствителен ли прогноз к значениям вырезывания,

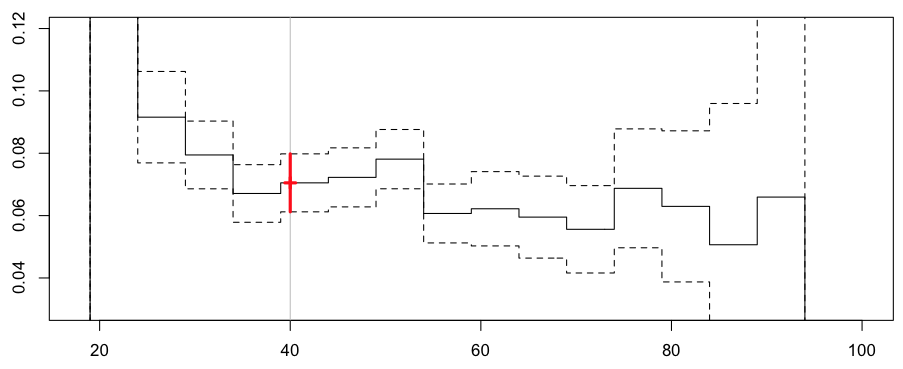
> level2=level1-2
> regglmc2=glm(nbre~cut(ageconducteur,level2)+offset(log(exposition)),
+ data=sinistres,family=poisson)

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-cut-2.png

что дает следующие значения для нашего 40-летнего водителя,

Frequency = 0.07050614  confidence interval 0.07980422 0.06120807

Поэтому здесь мы не устранили  проблему разрывов  . Идея здесь может состоять в том, чтобы рассмотреть  движущиеся регионы : если цель состоит в том, чтобы предсказать частоту для 40-летнего водителя, возможно, класс должен (каким-то образом) быть примерно 40. И центрировать интервал около 35 для водителей в возрасте 35 лет. И т.д.

  • Скользящая средняя

Таким образом, естественно рассмотреть некоторые  локальные  регрессии, где  должны рассматриваться только водители в возрасте почти 40 лет  . Это  почти  понятие связано с  пропускной способностью . Например, водителей между 35 и 45 можно считать почти 40. На практике мы можем либо рассмотреть функцию подмножества, либо мы можем использовать веса в регрессиях

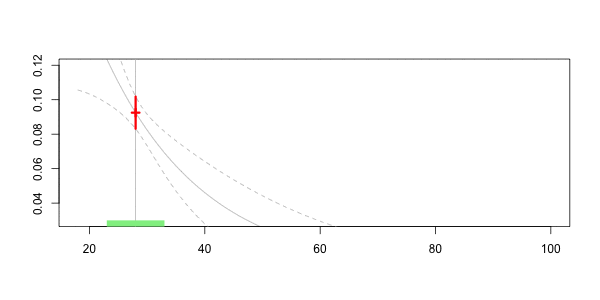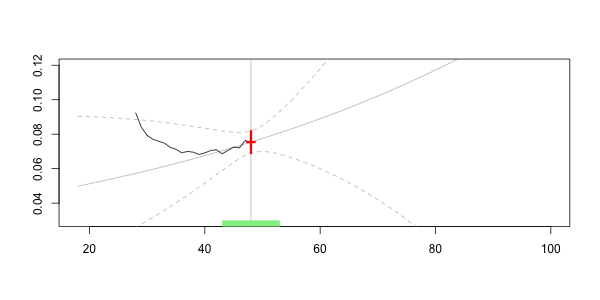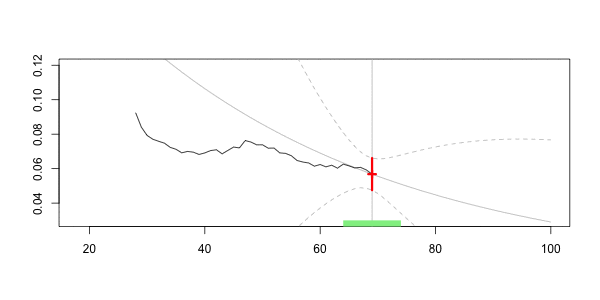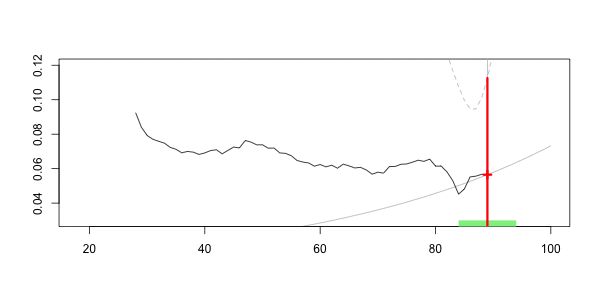
> value=40
> h=5
> sinistres$omega=(abs(sinistres$ageconducteur-value)<=h)*1
> regglmomega=glm(nbre~ageconducteur+offset(log(exposition)),
+ data=sinistres,family=poisson,weights=omega)

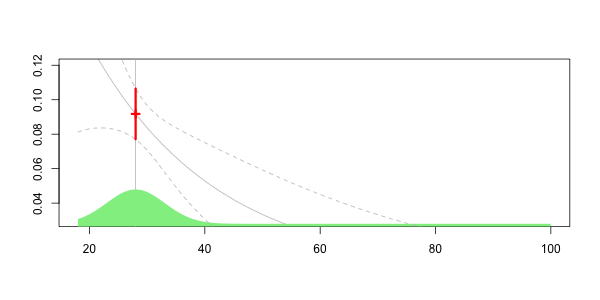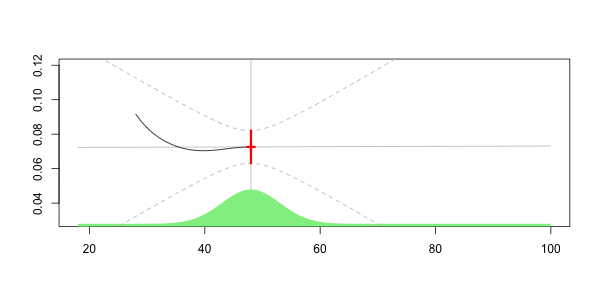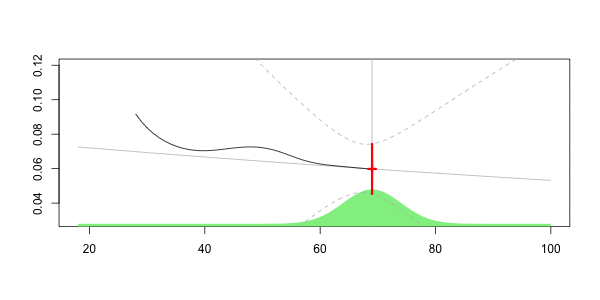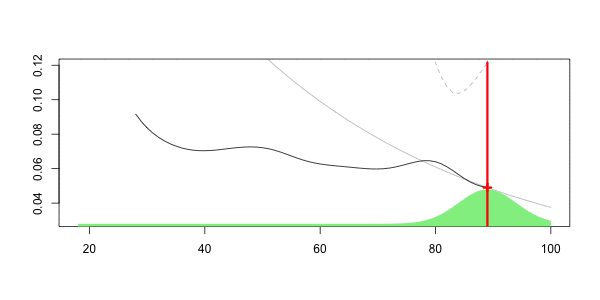
Чтобы увидеть, что происходит, давайте рассмотрим анимационный сюжет, где возраст интереса меняется,

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/liss-poisson-2.gif

Здесь, для нашего 40-летнего драйва, мы получаем

Frequency = 0.06913391  confidence interval 0.07535564 0.06291218

Мы получаем кривую, которую можно интерпретировать как  локальную  регрессию. Но здесь мы не учитываем, что 35 не так близко к 40, как могло бы быть 39. Здесь 34 предполагается очень далеким от 40. Ясно, что мы могли бы улучшить эту технику: можно рассмотреть функции ядра, то есть чем ближе к 40, тем больше вес.

> value=40
> h=5
> sinistres$omega=dnorm(abs(sinistres$ageconducteur-value)/h)
> regglmomega=glm(nbre~ageconducteur+offset(log(exposition)),
+ data=sinistres,family=poisson,weights=omega)

который может быть нанесен ниже

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/liss-poisson-1.gif

Здесь наш прогноз на наш 40-летний диск

Frequency = 0.07040464  confidence interval 0.07981521 0.06099408

Это идея методов  регрессии ядра . Но, как объясняется на слайдах, можно рассмотреть другие непараметрические методы, такие как сплайн-функции.

  • Сглаживание сплайнами

В R просто использовать функцию сплайна (как-то намного проще, чем сглаживание ядра)

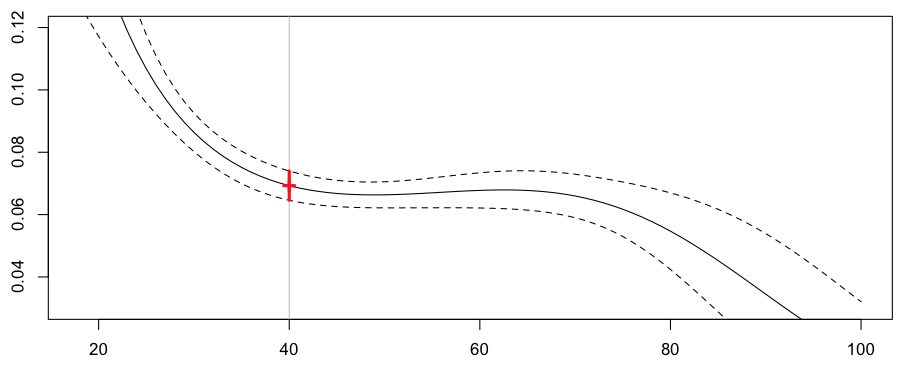
> library(splines)
> regglmbs=glm(nbre~bs(ageconducteur)+offset(log(exposition)),
+ data=sinistres,family=poisson)

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-splines.png

Прогноз для нашего 40-летнего водителя сейчас

Frequency = 0.06928169  confidence interval 0.07397124 0.06459215

Обратите внимание, что этот метод связан с другим классом моделей, так называемыми  обобщенными аддитивными моделями , то есть GAM.

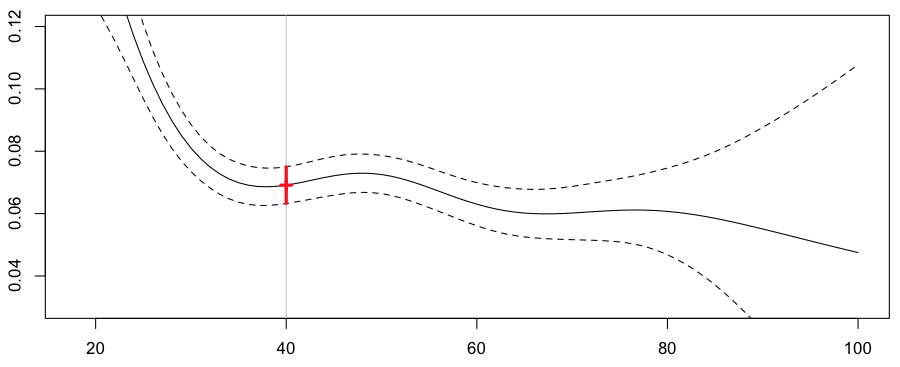
> library(mgcv)
> reggam=gam(nbre~s(ageconducteur)+offset(log(exposition)),
+ data=sinistres,family=poisson)

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/reg-poisson-gam.png

Прогноз очень близок к тому, который мы получили выше (основные различия наблюдаются для очень старых водителей)

Frequency = 0.06912683  confidence interval 0.07501663 0.06323702
  • Сравнение разных моделей

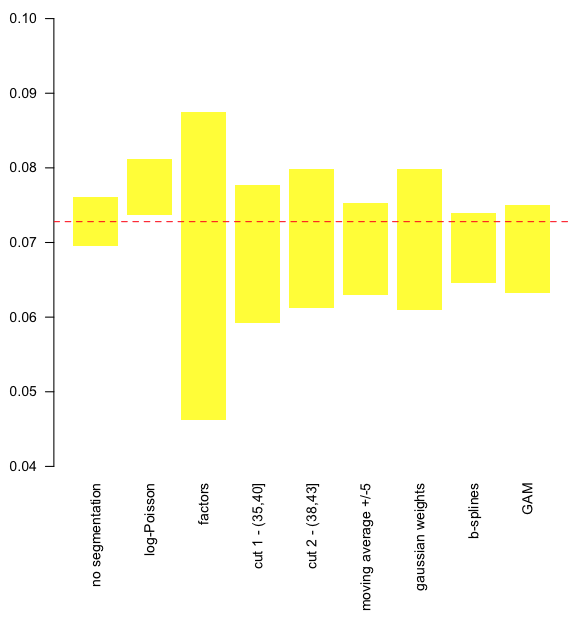
Somehow, one way or another, all those models are valid. So perhaps we should compare them,

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/Capture-d%E2%80%99e%CC%81cran-2013-02-05-a%CC%80-14.50.19.png

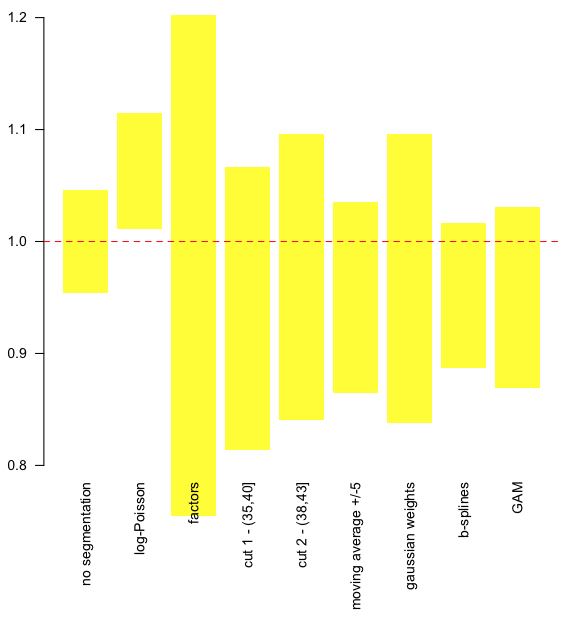
On the graph above, we can visualize the upper and the lower bound of the prediction, for the 9 models. The horizontal line is the predicted value without taking into account heterogeneity. It is possible to consider relative values, with respect to this value,

http://f.hypotheses.org/wp-content/blogs.dir/253/files/2013/02/Capture-d%E2%80%99e%CC%81cran-2013-02-05-a%CC%80-14.54.56.png

35
Share: