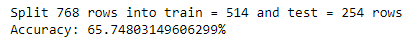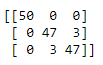Классификация и прогнозирование — два наиболее важных аспекта машинного обучения, а Наивный Байес — простой, но удивительно мощный алгоритм прогнозного моделирования. Итак, ребята, в этом наивном байесовском уроке я расскажу о следующих темах:
- Что такое наивный байесовский?
- Что такое теорема Байеса?
- Прогнозирование игры по теореме Байеса
- Наивный Байес в промышленности
- Пошаговая реализация наивного байесовского подхода
- Наивный байесовский с SKLEARN
Что такое наивный байесовский?
Наивный байесовский метод является одним из самых простых, но наиболее мощных алгоритмов классификации, основанных на теореме Байеса с предположением независимости среди предикторов. Наивная байесовская модель проста в построении и особенно полезна для очень больших наборов данных. Этот алгоритм состоит из двух частей:
-
наивный
-
байес
Наивный байесовский классификатор предполагает, что наличие функции в классе не связано с какой-либо другой функцией. Даже если эти признаки зависят друг от друга или от наличия других признаков, все эти свойства независимо способствуют вероятности того, что конкретный фрукт является яблоком, апельсином или бананом, и именно поэтому он известен как «Наивный». «.
Что такое теорема Байеса.
В статистике и теории вероятностей теорема Байеса описывает вероятность события, основываясь на предварительном знании условий, которые могут быть связаны с событием. Он служит способом определения условной вероятности.
Учитывая гипотезу ( H) и доказательство ( E) , теорема Байеса утверждает, что связь между вероятностью гипотезы до получения доказательства, P (H) , и вероятностью гипотезы после получения доказательства, P (H | Е) , это:
По этой причине P (H) называется априорной вероятностью , а P (H | E) называется апостериорной вероятностью . Коэффициент, который связывает два, P (H | E) / P (E) , называется отношением правдоподобия . Используя эти термины, теорема Байеса может быть перефразирована следующим образом:
«Апостериорная вероятность равна предыдущей вероятности, умноженной на отношение правдоподобия».
Немного смущен? Не беспокойся Давайте продолжим наш наивный байесовский урок и разберем эту концепцию с простой концепцией.
Пример теоремы Байеса
Предположим, у нас есть колода карт, и мы хотим выяснить вероятность того, что выбранная нами карта случайным образом окажется королем, учитывая, что это лицевая карта. Итак, согласно теореме Байеса, мы можем решить эту проблему. Для начала нам нужно выяснить вероятность:
- P (король) — 4/52, так как в колоде карт 4 короля.
- P (Face | King) равен 1, так как все короли являются лицевыми картами.
- P (Лицо) равно 12/52, так как в масти из 3 карт 3 карты и всего 4 масти.
Теперь, сложив все значения в уравнении Байеса, мы получаем результат 1/3 .
Прогнозирование игры по теореме Байеса
Давайте продолжим наш наивный байесовский урок и предскажем будущее с некоторыми погодными данными.
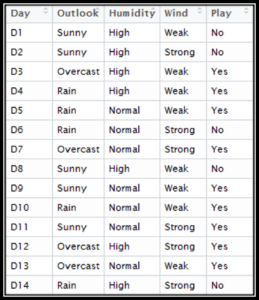
Здесь у нас есть наши данные, которые включают в себя день, прогноз, влажность и условия ветра. Последний столбец — «Играть», т. Е. Можем ли мы играть на улице, что мы должны предсказать.
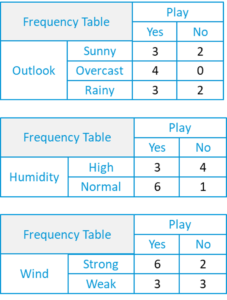
- Сначала мы создадим таблицу частот, используя каждый атрибут набора данных.
- Для каждой частотной таблицы мы сгенерируем таблицу вероятности .
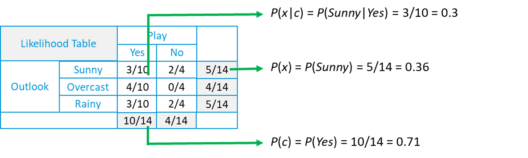
- Вероятность « Да » с учетом « Солнечного » составляет:
- P (c | x) = P (Да | Солнечно) = P (Солнечно | Да) * P (Да) / P (Солнечно) = (0,3 x 0,71) / 0,36 = 0,591
- Точно так же вероятность « Нет » данного « Солнечного » составляет:
- P (c | x) = P (Нет | Солнечный) = P (Солнечный | Нет) * P (Нет) / P (Солнечный) = (0,4 x 0,36) / 0,36 = 0,40
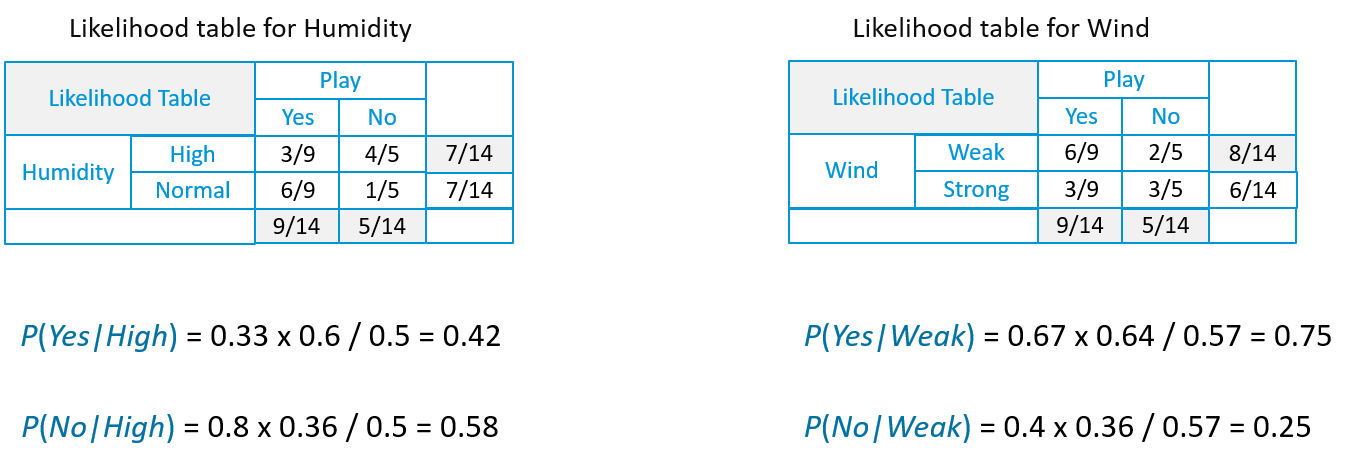
- Теперь точно так же нам нужно создать таблицу вероятностей и для других атрибутов.
Предположим, у нас есть День со следующими значениями:
-
Внешний вид = дождь
-
Влажность = Высокая
-
Ветер = Слабый
-
Play =?
Итак, с помощью данных мы должны предсказать, сможем ли мы играть в этот день или нет.
-
Вероятность «Да» в этот день = P (прогноз = дождь | да) * P (влажность = высокая | да) * P (ветер = слабый | да) * P (да)
-
= 2/9 * 3/9 * 6/9 * 9/14 = 0,0199
-
-
Вероятность «Нет» в этот день = P (прогноз = дождь | нет) * P (влажность = высокая | нет) * P (ветер = слабый | нет) * P (нет)
-
= 2/5 * 4/5 * 2/5 * 5/14 = 0,0166
-
Теперь, когда мы нормализуем значение, мы получаем:
- P (да) = 0,0199 / (0,0199+ 0,0166) = 0,55
- P (Нет) = 0,0166 / (0,0199+ 0,0166) = 0,45
Наша модель предсказывает, что с вероятностью 55% игра будет завтра.
Наивный Байес в промышленности
Теперь, когда у вас есть представление о том, что такое «наивный байесовский» и как он работает, давайте посмотрим, где он используется в промышленности.
RSS-каналы
Наш первый промышленный пример использования — категоризация новостей, или мы можем использовать термин «классификация текста», чтобы расширить спектр этого алгоритма. Новости в сети быстро растут, где каждый новостной сайт имеет свой собственный макет и категоризацию для группировки новостей. Компании используют веб-сканер для извлечения полезного текста из HTML-страниц новостных статей для создания полнотекстового RSS. Содержимое каждой новостной статьи маркируется (классифицируется). Чтобы добиться лучших результатов классификации, мы удаляем из документа менее значимые слова, то есть стоп. Мы применяем наивный байесовский классификатор для классификации новостного контента на основе новостного кода.
Фильтрация спама
Наивные байесовские классификаторы являются популярным статистическим методом фильтрации электронной почты. Как правило, они используют пакет слов / функций для идентификации спама в электронной почте — подход, обычно используемый в классификации текста. Наивные байесовские классификаторы работают, соотнося использование токенов (обычно слов или, иногда, других вещей) со спамом и не спамом, а затем, используя теорему Байеса, вычисляют вероятность того, что электронное письмо является или не является спамом.
Отдельные слова имеют особую вероятность появления в спаме и в законных письмах. Например, большинство пользователей электронной почты часто встречают слова «Лотерея» и «Удача» в спам-письмах, но редко видят их в других письмах. Каждое слово в письме влияет на вероятность спама в электронном письме или только на самые интересные слова. Этот вклад называется апостериорной вероятностью и вычисляется с использованием теоремы Бэйса . Затем вероятность спама в письме вычисляется по всем словам в письме, и если сумма превышает определенный порог (скажем, 95%), фильтр помечает письмо как спам.
Медицинский диагноз
В настоящее время современные больницы хорошо оснащены устройствами для мониторинга и сбора данных, что приводит к постоянному сбору огромного количества данных посредством медицинского осмотра и медицинского обслуживания. Одним из главных преимуществ наивного байесовского подхода, который привлекает врачей, является то, что «вся доступная информация используется для объяснения решения». Это объяснение кажется «естественным» для медицинской диагностики и прогноза, то есть близко к тому, как врачи диагностируют пациентов.
При работе с медицинскими данными наивный байесовский классификатор учитывает доказательства из многих атрибутов, чтобы сделать окончательный прогноз, и дает прозрачные объяснения своих решений, и поэтому он считается одним из наиболее полезных классификаторов для поддержки решений врачей.
Прогноз погоды
Используется байесовская модель для прогнозирования погоды, где апостериорные вероятности используются для вычисления вероятности каждой метки класса для экземпляра входных данных, а полученная с максимальной вероятностью считается итоговой.
Пошаговое внедрение наивного Байеса
Здесь у нас есть набор данных, состоящий из 768 наблюдений за женщинами в возрасте 21 года и старше. Набор данных описывает мгновенные измерения, взятые у пациентов, такие как возраст, обследование крови и количество беременностей. Каждая запись имеет классовое значение, которое указывает, перенес ли пациент диабет в течение 5 лет. Значения равны 1 для диабетиков и 0 для недиабетических.
Теперь давайте продолжим наш наивный байесовский урок и разберем все шаги, один за другим. Я разбил весь процесс на следующие шаги:
-
Обрабатывать данные
-
Обобщать данные
-
Делать предсказания
-
Оценить точность
Шаг 1: Обработка данных
Первое, что нам нужно сделать, это загрузить наш файл данных. Данные в формате CSV без строки заголовка или каких-либо кавычек. Мы можем открыть файл с помощью функции открытия и прочитать строки данных, используя функцию чтения в модуле CSV.
import csv
import math
import random
def loadCsv(filename):
lines = csv.reader(open(r'C:\Users\Kislay\Desktop\pima-indians-diabetes.data.csv'))
dataset = list(lines)
for i in range(len(dataset)):
dataset[i] = [float(x) for x in dataset[i]]
return datasetТеперь нам нужно разбить данные на наборы данных обучения и тестирования.
def splitDataset(dataset, splitRatio):
trainSize = int(len(dataset) * splitRatio)
trainSet = []
copy = list(dataset)
while len(trainSet) < trainSize:
index = random.randrange(len(copy))
trainSet.append(copy.pop(index))
return [trainSet, copy]Шаг 2: обобщить данные
Сводка собранных обучающих данных включает среднее значение и стандартное отклонение для каждого атрибута по значению класса. Они необходимы при создании прогнозов для расчета вероятности значений определенных атрибутов, принадлежащих каждому значению класса.
Мы можем разбить подготовку этих сводных данных на следующие подзадачи:
Отдельные данные по классу:
def separateByClass(dataset):
separated = {}
for i in range(len(dataset)):
vector = dataset[i]
if (vector[-1] not in separated):
separated[vector[-1]] = []
separated[vector[-1]].append(vector)
return separatedРассчитать среднее:
def mean(numbers):
return sum(numbers)/float(len(numbers))Рассчитать стандартное отклонение:
def stdev(numbers):
avg = mean(numbers)
variance = sum([pow(x-avg,2) for x in numbers])/float(len(numbers)-1)
return math.sqrt(variance)Суммируйте набор данных:
def summarize(dataset):
summaries = [(mean(attribute), stdev(attribute)) for attribute in zip(*dataset)]
del summaries[-1]
return summariesСуммируйте атрибуты по классам:
def summarizeByClass(dataset):
separated = separateByClass(dataset)
summaries = {}
for classValue, instances in separated.items():
summaries[classValue] = summarize(instances)
return summariesШаг 3: Создание прогнозов
Теперь мы готовы делать прогнозы, используя резюме, подготовленные на основе наших данных обучения. Прогнозирование включает в себя вычисление вероятности того, что данный экземпляр данных принадлежит каждому классу, затем выбор класса с наибольшей вероятностью в качестве прогнозирования. Нам необходимо выполнить следующие задачи:
Рассчитаем гауссову функцию плотности вероятности:
def calculateProbability(x, mean, stdev):
exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return (1/(math.sqrt(2*math.pi)*stdev))*exponentРассчитать класс вероятностей:
def calculateClassProbabilities(summaries, inputVector):
probabilities = {}
for classValue, classSummaries in summaries.items():
probabilities[classValue] = 1
for i in range(len(classSummaries)):
mean, stdev = classSummaries[i]
x = inputVector[i]
probabilities[classValue] *= calculateProbability(x, mean, stdev)
return probabilitiesСделать прогноз:
def predict(summaries, inputVector):
probabilities = calculateClassProbabilities(summaries, inputVector)
bestLabel, bestProb = None, -1
for classValue, probability in probabilities.items():
if bestLabel is None or probability > bestProb:
bestProb = probability
bestLabel = classValue
return bestLabelДелать предсказания:
def getPredictions(summaries, testSet):
predictions = []
for i in range(len(testSet)):
result = predict(summaries, testSet[i])
predictions.append(result)
return predictionsПолучить точность:
def getAccuracy(testSet, predictions):
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] == predictions[x]:
correct += 1
return (correct/float(len(testSet)))*100.0Наконец, мы определяем нашу основную функцию, где мы вызываем все эти методы, которые мы определили, один за другим, чтобы получить точность модели, которую мы создали.
def main():
filename = 'pima-indians-diabetes.data.csv'
splitRatio = 0.67
dataset = loadCsv(filename)
trainingSet, testSet = splitDataset(dataset, splitRatio)
print('Split {0} rows into train = {1} and test = {2} rows'.format(len(dataset),len(trainingSet),len(testSet)))
#prepare model
summaries = summarizeByClass(trainingSet)
#test model
predictions = getPredictions(summaries, testSet)
accuracy = getAccuracy(testSet, predictions)
print('Accuracy: {0}%'.format(accuracy))
main()Вывод:
Так что здесь, как вы можете видеть, точность нашей модели составляет 66%. Теперь это значение отличается от модели к модели, а также от коэффициента разделения.
Теперь, когда мы увидели шаги, включенные в наивный байесовский классификатор, Python поставляется с библиотекой Sckit-learn, которая делает все вышеупомянутые шаги простыми в реализации и использовании. Давайте продолжим наш наивный байесовский урок и посмотрим, как это можно реализовать.
Наивный Байес со Sckit-Learn

Импорт библиотек и загрузка наборов данных
from sklearn import datasets
from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
 
dataset = datasets.load_iris()Создание нашей наивной байесовской модели с использованием Sckit-learn
Здесь у нас есть GaussianNB() метод, который выполняет те же функции, что и код, описанный выше:
model = GaussianNB()
model.fit(dataset.data, dataset.target)Делать прогнозы
expected = dataset.target
predicted = model.predict(dataset.data)Получение точности и статистики
Здесь мы создадим отчет о классификации, который содержит различные статистические данные, необходимые для оценки модели. После этого мы создадим запутанную матрицу, которая даст нам четкое представление о точности и подгонке модели.
print(metrics.classification_report(expected, predicted))
print(metrics.confusion_matrix(expected, predicted))Классификационный отчет:
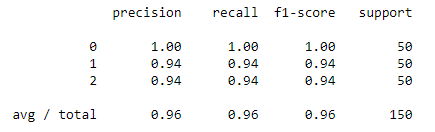
Как видите, с помощью этой мощной библиотеки сотни строк кода могут быть сведены в несколько строк кода.
Итак, на этом мы подошли к концу этого наивного байесовского урока. Поздравляю, ты больше не новичок в Наивном Байесе! Я надеюсь, вам понравился этот пост. Попробуйте этот простой пример на ваших системах сейчас.