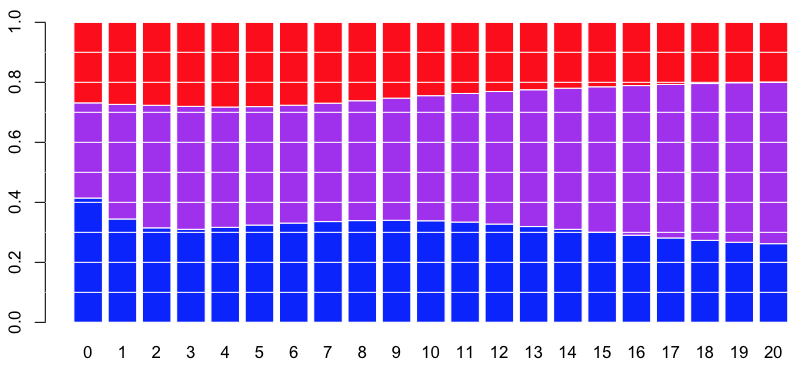
Обычно предложение, которое я повторяю на уроках регрессии, звучит так: « Пожалуйста, посмотрите на свои данные » В нашем предыдущем посте мы играли, как большинство эконометристов: мы не смотрели на данные. На самом деле, если мы посмотрим на распределение отдельных потерь, в наборе данных мы увидим следующее,
Похоже, в нашей базе данных есть претензии по фиксированным затратам . Как мы справляемся с этим в стандартном случае (например, в учебнике по модели потерь)? Мы можем использовать смесь — по крайней мере — три распределения здесь,
с
- распределение для мелких претензий
, например, экспоненциальное распределение
- масса Дирака в
, т.е.
- распределение для более крупных заявок,
например, гамма или логнормальное распределение
> I1=which(couts$cout<1120) > I2=which((couts$cout>=1120)&(couts$cout<1220)) > I3=which(couts$cout>=1220) > (p1=length(I1)/nrow(couts)) [1] 0.3284823 > (p2=length(I2)/nrow(couts)) [1] 0.4152807 > (p3=length(I3)/nrow(couts)) [1] 0.256237 > X=couts$cout > (kappa=mean(X[I2])) [1] 1171.998 > X0=X[I3]-kappa > u=seq(0,10000,by=20) > F1=pexp(u,1/mean(X[I1])) > F2= (u>kappa) > F3=plnorm(u-kappa,mean(log(X0)),sd(log(X0))) * (u>kappa) > F=F1*p1+F2*p2+F3*p3 > lines(u,F)
В нашем предыдущем посте мы обсуждали идею, что все параметры могут быть связаны с некоторыми ковариатами, т.е.
которые дают следующую премиум-модель,
Для 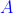
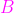

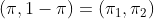
т.е.
и
Чтобы получить многомерное расширение, напишите
и
Опять же, методы максимального правдоподобия могут быть использованы, так как
где здесь переменная, 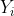
и, что касается логистической регрессии, то используйте алгоритм Ньютона Рафсона для численного расчета максимальной вероятности. В R сначала нужно определить уровни, например
> seuils=c(0,1120,1220,1e+12) > couts$tranches=cut(couts$cout,breaks=seuils, + labels=c("small","fixed","large")) > head(couts,5) nocontrat no garantie cout exposition zone puissance agevehicule 1 1870 17219 1RC 1692.29 0.11 C 5 0 2 1963 16336 1RC 422.05 0.10 E 9 0 3 4263 17089 1RC 549.21 0.65 C 10 7 4 5181 17801 1RC 191.15 0.57 D 5 2 5 6375 17485 1RC 2031.77 0.47 B 7 4 ageconducteur bonus marque carburant densite region tranches 1 52 50 12 E 73 13 large 2 78 50 12 E 72 13 small 3 27 76 12 D 52 5 small 4 26 100 12 D 83 0 small 5 46 50 6 E 11 13 large
Затем мы можем запустить полиномиальную регрессию , из
> library(nnet)
используя некоторые выбранные ковариаты
> reg=multinom(tranches~ageconducteur+agevehicule+zone+carburant,data=couts) # weights: 30 (18 variable) initial value 2113.730043 iter 10 value 2063.326526 iter 20 value 2059.206691 final value 2059.134802 converged
Выход здесь
> summary(reg) Call: multinom(formula = tranches ~ ageconducteur + agevehicule + zone + carburant, data = couts) Coefficients: (Intercept) ageconducteur agevehicule zoneB zoneC fixed -0.2779176 0.012071029 0.01768260 0.05567183 -0.2126045 large -0.7029836 0.008581459 -0.01426202 0.07608382 0.1007513 zoneD zoneE zoneF carburantE fixed -0.1548064 -0.2000597 -0.8441011 -0.009224715 large 0.3434686 0.1803350 -0.1969320 0.039414682 Std. Errors: (Intercept) ageconducteur agevehicule zoneB zoneC zoneD fixed 0.2371936 0.003738456 0.01013892 0.2259144 0.1776762 0.1838344 large 0.2753840 0.004203217 0.01189342 0.2746457 0.2122819 0.2151504 zoneE zoneF carburantE fixed 0.1830139 0.3377169 0.1106009 large 0.2160268 0.3624900 0.1243560
Чтобы визуализировать влияние ковариаты (один, только), можно использовать также сплайн-функции
> library(splines) > reg=multinom(tranches~agevehicule,data=couts) # weights: 9 (4 variable) initial value 2113.730043 final value 2072.462863 converged > reg=multinom(tranches~bs(agevehicule),data=couts) # weights: 15 (8 variable) initial value 2113.730043 iter 10 value 2070.496939 iter 20 value 2069.787720 iter 30 value 2069.659958 final value 2069.479535 converged
Например, если ковариата — это возраст автомобиля, у нас есть следующие вероятности
> predict(reg,newdata=data.frame(agevehicule=5),type="probs") small fixed large 0.3388947 0.3869228 0.2741825
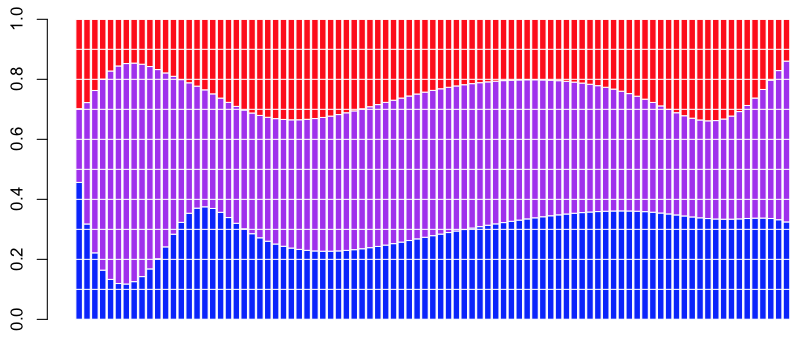
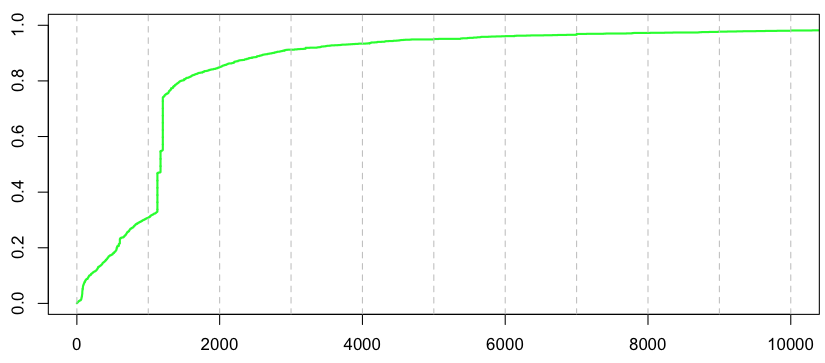
и для всех возрастов от 0 до 20 лет,
Например, для новых автомобилей доля постоянных затрат довольно мала (здесь фиолетовым цветом) и продолжает увеличиваться с возрастом автомобиля. Если ковариата — это плотность населения в районе, где живет водитель, мы получаем следующие вероятности
> reg=multinom(tranches~bs(densite),data=couts) # weights: 15 (8 variable) initial value 2113.730043 iter 10 value 2068.469825 final value 2068.466349 converged > predict(reg,newdata=data.frame(densite=90),type="probs") small fixed large 0.3484422 0.3473315 0.3042263
На основании этих вероятностей можно затем рассчитать ожидаемую стоимость претензии, учитывая некоторые ковариаты (например, плотность). Но сначала определим подмножества всего набора данных
> sbaseA=couts[couts$tranches=="small",] > sbaseB=couts[couts$tranches=="fixed",] > sbaseC=couts[couts$tranches=="large",]
с порогом, заданным
> (k=mean(sousbaseB$cout)) [1] 1171.998
Тогда давайте запустим наши четыре модели,
> reg=multinom(tranches~bs(densite),data=couts) > regA=glm(cout~bs(densite),data=sousbaseA,family=Gamma(link="log")) > regB=glm(cout~1,data=sousbaseB,family=Gamma(link="log")) > regC=glm((cout-k)~bs(densite),data=sousbaseC,family=Gamma(link="log"))
Теперь мы можем вычислить прогнозы на основе этих моделей,
> nouveau=data.frame(densite=seq(10,100)) > proba=predict(reg,newdata=nouveau,type="probs") > predA=predict(regA,newdata=nouveau,type="response") > predB=predict(regB,newdata=nouveau,type="response") > predC=predict(regC,newdata=nouveau,type="response")+k > pred=cbind(predA,predB,predC)
Чтобы визуализировать влияние каждого компонента на премию, мы можем вычислить вероятности, а также ожидаемые затраты (учитывая стоимость в каждом подмножестве)
> cbind(proba,pred)[seq(10,90,by=10),]
small fixed large predA predB predC
10 0.3344014 0.4241790 0.2414196 423.3746 1171.998 7135.904
20 0.3181240 0.4471869 0.2346892 428.2537 1171.998 6451.890
30 0.3076710 0.4626572 0.2296718 438.5509 1171.998 5499.030
40 0.3032872 0.4683247 0.2283881 451.4457 1171.998 4615.051
50 0.3052378 0.4620219 0.2327404 463.8545 1171.998 3961.994
60 0.3136136 0.4417057 0.2446807 472.3596 1171.998 3586.833
70 0.3279413 0.4056971 0.2663616 473.3719 1171.998 3513.601
80 0.3464842 0.3534126 0.3001032 463.5483 1171.998 3840.078
90 0.3652932 0.2868006 0.3479061 440.4925 1171.998 4912.379
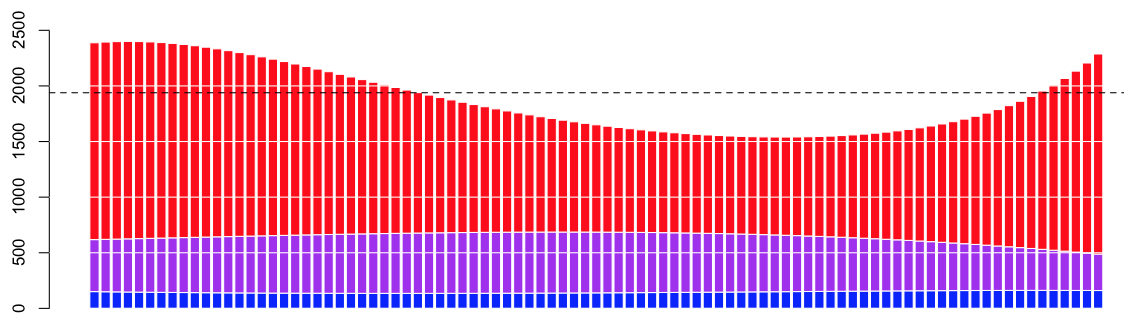
Теперь можно построить эти цифры на графике,
> barplot(t(proba*pred)) > abline(h=mean(couts$cout),lty=2)
(пунктирная горизонтальная линия — это средняя стоимость заявки в нашем наборе данных).
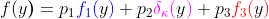
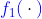 , например, экспоненциальное распределение
, например, экспоненциальное распределение , т.е.
, т.е. 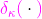
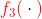 например, гамма или логнормальное распределение
например, гамма или логнормальное распределение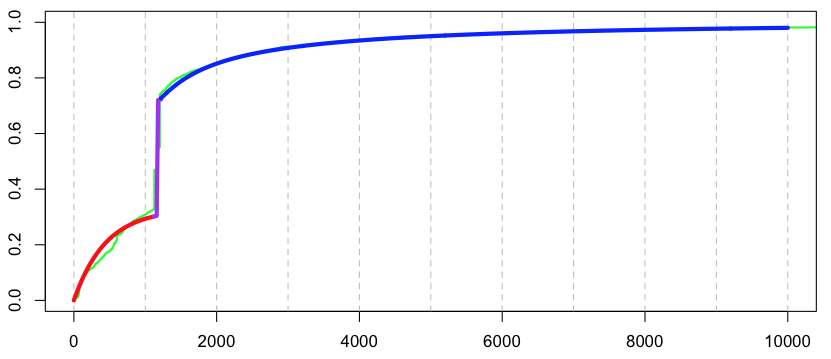
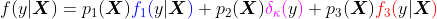
![http://latex.codecogs.com/gif.latex?\mathbb{E}(Y|\boldsymbol{X})%20=%20{\color{Blue}%20{\underbrace{\mathbb{E} (Y | \ boldsymbol {X}, Y \ Leq% 20s_1)} _ {А}% 20 \ CDOT% 20 {\ underbrace {\ mathbb {P} (Y \ Leq% 20s_1 | \ boldsymbol {X})} _ {D}}}} \\ + {\ {цвет фиолетовый}% 20 {{\ underbrace {\ mathbb {Е} (Y | Y \ в (% 20s_1, s_2],% 20 \ boldsymbol {X})% 20 } _ {в}} \ CDOT% 20 {\ underbrace {\ mathbb {P} (Y \ в (% 20s_1, s_2] |% 20 \ boldsymbol {X})} _ {D}}}} \\ + { \ цвет {Красный}% 20 {{\ underbrace {\ mathbb {Е} (Y | Y% 3E% 20s_2,% 20 \ boldsymbol {X})% 20} _ {C}} \ CDOT% 20 {\ underbrace { \ mathbb {P} (Y% 3E% 20s_2 |% 20 \ boldsymbol {X})} _ {D}}}}](/wp-content/uploads/images/dzo/1bd05c186c042494cdcc16164f6469e9.latex)
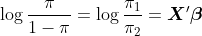
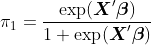
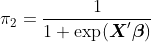
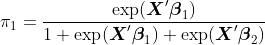
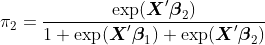
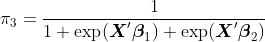
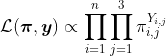
![http://latex.codecogs.com/gif.latex?\log%20\mathcal{L}(\boldsymbol{\beta},\boldsymbol{y})\propto%20\sum_{i=1}^n % 20 \ sum_ {J = 1} ^ 2% 20 \ влево (Y_ {I, J}% 20 \ boldsymbol {X}% 27-i \ boldsymbol {\ бета} _j \ справа)% 20-% 20n_i \ войти \ левый [1 + 1 + \ ехр (\ boldsymbol {X}% 27 \ boldsymbol {\ бета} -1) + \ ехр (\ boldsymbol {X}% 27 \ boldsymbol {\ бета} _2) \ вправо]](/wp-content/uploads/images/dzo/43360b6868551beb7bdc9b8e442a2d61.latex)