Вчера я загрузил сообщение, в котором пытался показать, что «стандартные» регрессионные модели не работают плохо. По крайней мере, если вы включите сплайны (многомерные сплайны) для учета совместных эффектов и нелинейностей. До сих пор я не обсуждал возможное большое количество функций (но с помощью процедур начальной загрузки можно оценить что-то, связанное с переменной важностью, что нравится людям из машинного обучения).
Но мой пост был неполным: я просто рисовал прогноз, полученный какой-то моделью. И это «выглядело», как регрессия была хороша, как и случайный форрест, ближайший сосед и алгоритм повышения. Что если мы сравним эти модели по новым данным?
Вот код для создания всех моделей (я включил еще одну, своего рода эталонный тест, в который не включены никакие ковариаты), основанный на 1000 моделируемых значениях
> n <- 1000
> set.seed(1)
> rtf <- function(a1, a2) { sin(a1+a2)/(a1+a2) }
> df <- data.frame(x1=(runif(n, min=1, max=6)),
+ x2=(runif(n, min=1, max=6)))
> df$m <- rtf(df$x1, df$x2)
> df$y <- df$m+rnorm(n,sd=.1)
> model_cste <- lm(y~1,data=df)
> p_cste <- function(x1,x2) predict(model_cste,newdata=data.frame(x1=x1,x2=x2))
> model_lm <- lm(y~x1+x2,data=df)
> p_lm <- function(x1,x2) predict(model_lm,newdata=data.frame(x1=x1,x2=x2))
> library(mgcv)
> model_bs <- gam(y~s(x1,x2),data=df)
> p_bs <- function(x1,x2) predict(model_bs,newdata=data.frame(x1=x1,x2=x2))
> library(rpart)
> model_cart <- rpart(y~x1+x2,data=df,method="anova")
> p_cart <- function(x1,x2) predict(model_cart,newdata=data.frame(x1=x1,x2=x2),type="vector")
> library(randomForest)
> model_rf <- randomForest(y~x1+x2,data=df)
> p_rf <- function(x1,x2) as.numeric(predict(model_rf,newdata=
+ data.frame(x1=x1,x2=x2),type="response"))
> k <- 10
> p_knn <- function(x1,x2){
+ d <- (df$x1-x1)^2+(df$x2-x2)^2
+ return(mean(df$y[which(rank(d)<=k)]))
+ }
> library(dismo)
> model_gbm <- gbm.step(data=df, gbm.x = 1:2, gbm.y = 4,
+ family = "gaussian", tree.complexity = 5,
+ learning.rate = 0.01, bag.fraction = 0.5)
GBM STEP - version 2.9
Performing cross-validation optimisation of a boosted regression tree model
for y and using a family of gaussian
Using 1000 observations and 2 predictors
creating 10 initial models of 50 trees
folds are unstratified
total mean deviance = 0.0242
tolerance is fixed at 0
ntrees resid. dev.
50 0.0195
now adding trees...
100 0.017
150 0.0154
200 0.0145
250 0.0139(и т.д)
1650 0.0123
fitting final gbm model with a fixed number of 1150 trees for y
mean total deviance = 0.024
mean residual deviance = 0.009
estimated cv deviance = 0.012 ; se = 0.001
training data correlation = 0.804
cv correlation = 0.705 ; se = 0.013
elapsed time - 0.11 minutes
> p_boost <- function(x1,x2) predict(model_gbm,newdata=data.frame(x1=x1,x2=x2),n.trees=1200)Чтобы протестировать эти модели на новых данных (на самом деле это цель прогностической модели, которая позволяет построить обобщенную модель, которая хорошо работает с новыми данными), сгенерируйте еще одну выборку
> n <- 500
> df_new <- data.frame(x1=(runif(n, min=1, max=6)), x2=(runif(n, min=1, max=6)))
> df_new$m <- rtf(df_new$x1, df_new$x2)
> df_new$y <- df_new$m+rnorm(n,sd=.1)А затем сравните наблюдаемые значения с предсказанными. Например, на графике
> output_model <- function(p=Vectorize(p_knn)){
+ plot(df_new$y,p(df_new$x1,df_new$x2),ylim=c(-.45,.45),xlim=c(-.45,.45),xlab="Observed",ylab="Predicted")
+ abline(a=0,b=1,lty=2,col="grey")
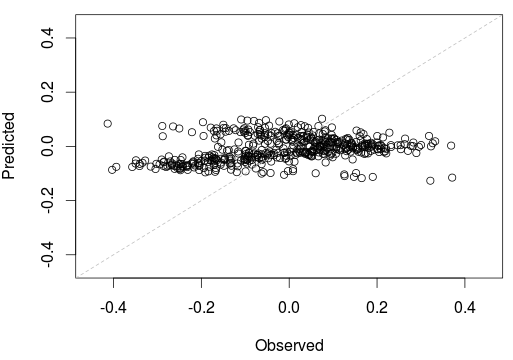
+ }Для линейной модели получаем
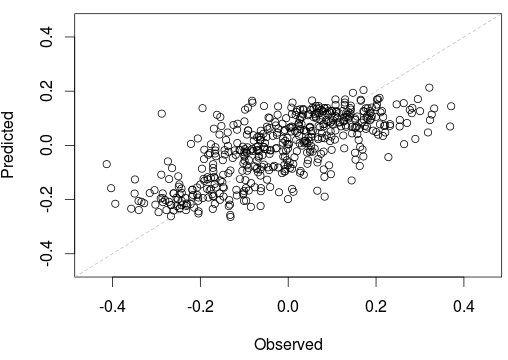
> output_model(Vectorize(p_lm))Для k-ближайшего соседа мы получаем
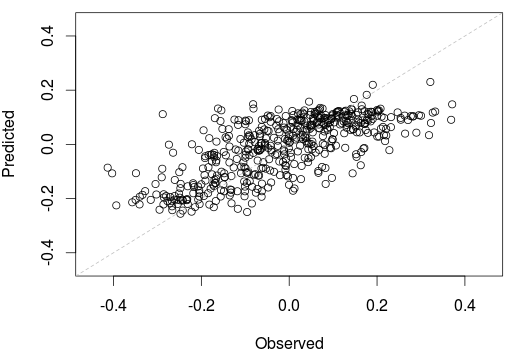
> output_model(Vectorize(p_knn))С нашей усиленной моделью мы получаем
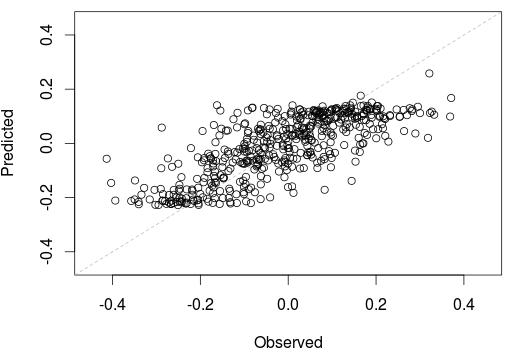
> output_model(Vectorize(p_boost))И, наконец, с нашими двумерными сплайнами, мы получаем
> output_model(Vectorize(p_bs))Также возможно учитывать некоторое расстояние, например, стандартное расстояние,
> sum_error_2 <- function(name_model){
+ sum( (df_new$y - Vectorize(get(name_model))(df_new$x1,df_new$x2))^2 )
+ }Здесь мы вводим имя функции прогнозирования (не объект R, мы скоро увидим, почему) в качестве параметра нашей функции. Чтобы получить достоверное заключение, почему бы не сгенерировать сотни новых выборок и не вычислить расстояние по ошибке.
> L2 <- NULL
> for(s in 1:100){
+ n <- 500
+ df_new <- data.frame(x1=(runif(n, min=1, max=6)), x2=(runif(n, min=1, max=6)))
+ df_new$m <- rtf(df_new$x1, df_new$x2)
+ df_new$y <- df_new$m+rnorm(n,sd=.1)
+ list_models <- c("p_cste","p_lm","p_bs","p_cart","p_rf","p_knn","p_boost")
+ L2_error <- sapply(list_models,sum_error_2)
+ L2 <- rbind(L2,L2_error)
+ }Чтобы сравнить наши предикторы, используйте
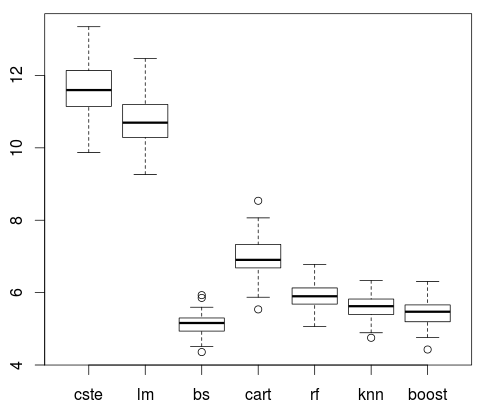
> colnames(L2) <- substr(colnames(L2),3,nchar(colnames(L2)))
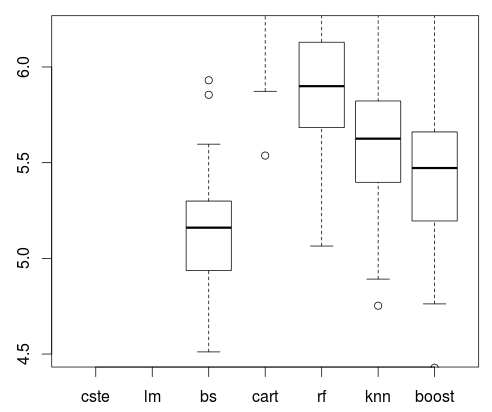
> boxplot(L2)Наша модель линейной регрессии неэффективна ( лм ). Ясно. Но мы видели это уже вчера. И наша двумерная модель сплайна ( бс ). На самом деле, это даже работает лучше , что все другие модели рассматриваются здесь ( ВЧ , КННЫ и даже подталкивание ).
boxplot(L2,ylim=c(4.5,6.2))После моего предыдущего поста было много дискуссий, комментариев и Twitter. Я видел, что должен быть какой-то компромисс: интерпретируемость (эконометрические модели) и точность (машинное обучение). Это явно не так просто. Простая модель регрессии со сплайнами может работать лучше, чем любой алгоритм машинного обучения, из того, что мы видели здесь.