Кластеризация — это очень распространенный метод необученного машинного обучения, позволяющий обнаруживать группы данных, которые «находятся рядом» друг с другом. Он широко используется в сегментации клиентов и обнаружении выбросов.
Он основан на некотором понятии «расстояние» (обратное сходство) между точками данных и используется для определения точек данных, которые находятся рядом друг с другом. Далее мы обсудим некоторые очень простые алгоритмы для создания кластеров и используем R в качестве примеров.
K-средних
Это самый основной алгоритм
- Выберите начальный набор из K центроидов (это может быть случайным или любым другим способом)
- Для каждой точки данных назначьте ее члену ближайшего центроида в соответствии с заданной функцией расстояния
- Отрегулируйте положение центроида как среднее значение всех назначенных ему точек данных. Вернитесь к (2), пока членство не изменится и положение центроида не станет стабильным.
- Выведите центроиды.
Обратите внимание, что в K-средних нам требуется не только определение функции расстояния, но и определение средней функции. Конечно, нам также нужно указать K (количество центроидов).
K-Means отлично масштабируется с O (n * k * r), где r — количество раундов, которое является константой, зависящей от начального выбора центроидов. Также обратите внимание, что результат каждого раунда является неопределенным. Обычная практика состоит в том, чтобы запустить несколько раундов K-Means и выбрать результат лучшего раунда. Лучший раунд — тот, кто минимизирует среднее расстояние каждой точки до назначенного центроида.
Вот пример выполнения K-Means в R
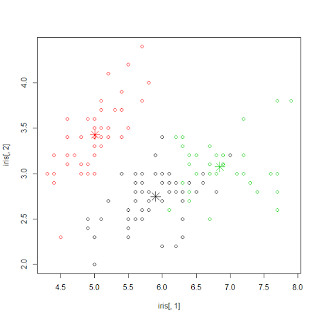
> km <- kmeans(iris[,1:4], 3) > plot(iris[,1], iris[,2], col=km$cluster) > points(km$centers[,c(1,2)], col=1:3, pch=8, cex=2) > table(km$cluster, iris$Species) setosa versicolor virginica 1 0 48 14 2 50 0 0 3 0 2 36
со следующим визуальным выводом.
Иерархическая кластеризация
При таком подходе он сравнивает все пары точек данных и объединяет ту, которая находится на самом близком расстоянии.
- Вычислить расстояние между каждой парой точки / кластера. Вычислить расстояние между точкой A и точкой B — это просто функция расстояния. Вычисление расстояния между точкой A до кластера B может включать множество вариантов (например, расстояние min / max / avg между точкой A и точками в кластере B). Вычислить расстояние между кластером A и кластером B можно сначала вычислить расстояние для всех пар точек (одна от кластера A, а другая от кластера B), а затем выбрать либо min / max / avg из этих пар.
- Объедините две ближайшие точки / кластер в кластер. Вернитесь к (1), пока не останется только один большой кластер.
В иерархической кластеризации сложность O (n ^ 2), на выходе будет дерево шагов слияния. Нам не требуется указывать K или среднее значение. Из-за высокой сложности иерархическая кластеризация обычно используется, когда число точек не слишком велико.
Вот пример выполнения иерархической кластеризации в R
> sampleiris <- iris[sample(1:150, 40),] > distance <- dist(sampleiris[,-5], method="euclidean") > cluster <- hclust(distance, method="average") > plot(cluster, hang=-1, label=sampleiris$Species)
со следующим визуальным выводом
Нечеткие С-средства
В отличие от K-средних, где каждая точка данных принадлежит только одному кластеру, в нечетких значениях каждая точка данных имеет долю членства в каждом кластере. Цель состоит в том, чтобы выяснить долю членов, которые минимизируют ожидаемое расстояние до каждого центроида. Алгоритм очень похож на K-Means, за исключением того, что используется матрица (строка — каждая точка данных, столбец — каждая центроид, а каждая ячейка — степень принадлежности).
- Инициализировать матрицу членства U
- Повторите шаги (3), (4), пока не сходятся
- Вычислить местоположение каждого центроида на основе взвешенной доли местоположения его элемента данных.
- Обновите каждую ячейку следующим образом
Обратите внимание, что параметр m является степенью нечеткости. Выходными данными является матрица, в которой каждой точке данных присваивается степень принадлежности к каждому центроиду.
Вот пример выполнения нечетких c-средних в R
> library(e1071)
> result <- cmeans(iris[,-5], 3, 100, m=2, method="cmeans")
> plot(iris[,1], iris[,2], col=result$cluster)
> points(result$centers[,c(1,2)], col=1:3, pch=8, cex=2)
> result$membership[1:3,]
1 2 3
[1,] 0.001072018 0.002304389 0.9966236
[2,] 0.007498458 0.016651044 0.9758505
[3,] 0.006414909 0.013760502 0.9798246
> table(iris$Species, result$cluster)
1 2 3
setosa 0 0 50
versicolor 3 47 0
virginica 37 13 0
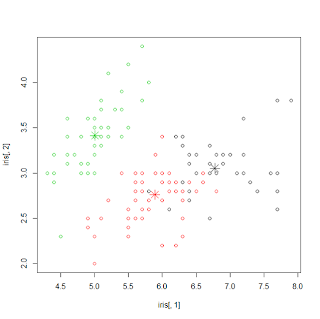
со следующим визуальным выводом (очень похоже на K-Means)
Мультигауссовский с максимизацией ожидания
Как правило, в машинном обучении мы будем изучать набор параметров, которые максимизируют вероятность наблюдения наших данных обучения. Однако, что если в наших данных есть какая-то скрытая переменная, которую мы не наблюдали. Максимизация ожиданий — очень распространенный метод использования параметра для оценки распределения вероятностей этих скрытых переменных, вычисления ожидаемой вероятности и затем определения параметров, которые максимизируют эту ожидаемую вероятность. Это можно объяснить следующим образом …
Теперь мы предполагаем, что базовое распределение данных основано на K центроидах, каждый из которых является многовариантным распределением Гаусса. Чтобы отобразить Ожидание / Максимизация в это, мы имеем следующее.
Порядок сложности аналогичен K-средним с большей константой. Это также требует, чтобы K был указан. В отличие от K-средних, кластер которых всегда имеет круглую форму. Мультигауссовский может обнаружить кластер с эллиптической формой с различной ориентацией, и, следовательно, он является более общим, чем K-средние.
Вот пример выполнения мультигауссова с EM в R
> library(mclust)
> mc <- Mclust(iris[,1:4], 3)
> plot(mc, data=iris[,1:4], what=c('classification'),
dimens=c(3,4))
> table(iris$Species, mc$classification)
1 2 3
setosa 50 0 0
versicolor 0 45 5
virginica 0 0 50
со следующим визуальным выводом
Кластер на основе плотности
В кластере на основе плотности кластер проходит вдоль распределения плотности. Важны два параметра: «eps» определяет радиус окрестности каждой точки, а «minpts» — это количество соседей в моем радиусе «eps». Основной алгоритм DBscan работает следующим образом
- Первое сканирование: для каждой точки вычислите расстояние со всеми остальными точками. Увеличьте число соседей, если оно меньше «eps».
- Второе сканирование: для каждой точки пометьте ее как основную точку, если число соседей превышает «minpts»
- Третье сканирование: для каждой базовой точки, если она еще не назначена кластеру, создайте новый кластер и назначьте его этой базовой точке, а также всем ее соседям в радиусе «eps».
В отличие от других кластеров, кластер на основе плотности может иметь некоторые выбросы (точки данных, которые не принадлежат ни к каким кластерам). С другой стороны, он может обнаружить кластер произвольной формы (совсем не обязательно должен быть круглым).
Вот пример выполнения DBscan в R
> library(fpc) # eps is radius of neighborhood, MinPts is no of neighbors # within eps > cluster <- dbscan(sampleiris[,-5], eps=0.6, MinPts=4) > plot(cluster, sampleiris) > plot(cluster, sampleiris[,c(1,4)]) # Notice points in cluster 0 are unassigned outliers > table(cluster$cluster, sampleiris$Species) setosa versicolor virginica 0 1 2 6 1 0 13 0 2 12 0 0 3 0 0 6
со следующим визуальным выводом … (обратите внимание, что черные точки являются выбросами, треугольники являются центральными точками, а круги являются граничными точками)
Хотя это охватывает несколько способов поиска кластеров, это не исчерпывающий список. Также здесь я попытался проиллюстрировать основную идею и использовать R в качестве примера. Для действительно большого набора данных нам может потребоваться запустить алгоритм кластеризации параллельно. Вот мой предыдущий блог о том, как сделать K-Means, используя Map / Reduce, а также кластеризацию Canopy.