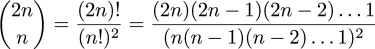
k-регулярные графики: строковые генераторы k-Ary

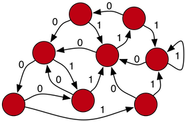
k— регулярным , если каждая вершина имеет k смежные вершины. Начиная с любой вершины, есть возможный -длин путь в -регулярного графика. Для 2-регулярного графа ( ) число уникальных путей эквивалентно количеству объектов, которые могут быть представлены двоичной строкой . Например, в 2-регулярном графе имеется 4 294 967 296 путей длиной 32 ( ). Эта взаимосвязь очевидна, если для всех инцидентных ребер вершины помечены либо 0, либо 1. Если траверсеры печатают метку ребра на каждом шаге в пошаговом обходе, то будут сгенерированы все возможные двоичные строки длины.knnkk=2232nn
Граф с 2- степени вершин редки в природе . 
k-регулярность встречается редко. 10-регулярный граф имеет 100 000 000 000 000 000 000 000 000 000 000 уникальных путей длиной 32 ( ). Комбинаторные взрывы очевидны при вычислении на естественных графах . Такие истины влияют на способ реализации технологий / алгоритмов при решении реальных графовых задач.1032
Решетчатые графы: двоичные строки с равным числом 0 и 1

20x20 Направлена решетка имеет 441 вершин и ребер 840. Как показано аналитически в оригинальном сообщении Loopy Lattices , существует 137 846 528 820 (137,85 миллиардов) уникальных путей от верхней левой вершины до нижней правой вершины. Дискретный путешественник должен совершить путешествие за 40 шагов. Из этих 40 шагов будет напечатано равное количество единиц и нулей. Таким образом, проблема определения количества уникальных путей в 20x20решетка — это вопрос о том, сколько существует уникальных двоичных строк длиной 40, так что существует одинаковое количество единиц и нулей. Это ограничение дает число, которое намного меньше, чем . В предыдущем посте Гремлин (в его глубинной, перечислительной форме) не смог вычислить ответ из-за взрыва возможностей. Поэтому, чтобы ответить на вопрос, ниже было предоставлено закрытое решение . Решение гласит: « 2n выбрать n » или, в частности, «40 выбрать 20». 20 выбранных 1 слотов в двоичной строке длиной 40 заставляют оставшиеся 20 позиций быть равными 0.kn
Титан против Фавна: счетное / счетное различие
Базы данных графа , такие как Титан может быть использован для хранения 20x20 решетку. Несмотря на то, что граф ребер 840 чрезвычайно мал для « базы данных », необходимо провести эксперимент. Код Gremlin / Groovy для создания 20x20 решетки в Titan приведен ниже.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
defgenerateLattice(n) {
g = TitanFactory.open('bin/cassandra.local')
// total number of vertices
max= Math.pow((n+1),2)
// generate the vertices
vertices = [];
(1..max).each{ vertices.add(g.addVertex()) }
// generate the edges
vertices.eachWithIndex{ v, i ->
right = i + 1
if(((right % (n + 1)) > 0) && (right <= max)) {
v.addEdge('link', vertices[right])
}
down = i + n + 1
if(down < max) {
v.addEdge('link', vertices[down])
}
}
g.commit();
returng
}
|
Пройдя через решетку с титаном

20x20решетке. Обход длины 40 — это полный обход решетки от верхнего левого угла до нижнего правого. Код обхода и время выполнения приведены ниже. Потенцируя выполнения реализуются: 10,9 минут (28 шагов), 2,3 часа (29 шагов), и 9,8 часа (30 шагов) обходы. Расчет был остановлен на 31-м шаге. Число путей длиной 40 не может быть разумно рассчитано с помощью Titan / Gremlin. Путем исчерпывающего перечисления путей и с ростом числа путей в геометрической прогрессии по мере увеличения длины пути вычисление этой формы обречено на большие значения n.
/usr/local/titan-all-0.3.1$ bin/gremlin.sh
\,,,/
(o o)
-----oOOo-(_)-oOOo-----
gremlin> g = generateLattice(20)
==>titangraph[cassandrathrift:127.0.0.1]
gremlin> g.V.count()
==>441
gremlin> g.E.count()
==>840
gremlin> (1..40).each{ l ->
t = System.currentTimeMillis();
c = g.v(4).out.loop(1){it.loops <= l}.count()
t = System.currentTimeMillis() - t;
println(l + ":" + c + ":" + t)
}
| длина пути | количество путей | время прохождения (мс) | длина пути | количество путей | время прохождения (мс) |
|---|---|---|---|---|---|
| 1 | 2 | 9 | 2 | 4 | 2 |
| 3 | 8 | 1 | 4 | 16 | 2 |
| 5 | 32 | 3 | 6 | 64 | 5 |
| 7 | 128 | 10 | 8 | 256 | 17 |
| 9 | 512 | 36 | 10 | 1024 | 62 |
| 11 | 2048 | 74 | 12 | 4096 | 96 |
| 13 | 8192 | 49 | 14 | 16384 | 61 |
| 15 | 32768 | 88 | 16 | 65536 | 163 |
| 17 | 131072 | 325 | 18 | 262144 | 646 |
| 19 | 524288 | 1296 | 20 | 1048576 | 2573 |
| 21 | 2097150 | 5172 | 22 | 4194258 | 10306 |
| 23 | 8388054 | 20659 | 24 | 16772566 | 41555 |
| 25 | 33523880 | 82993 | 26 | 66941500 | 166828 |
| 27 | 133422540 | 331954 | 28 | 265069020 | 654070 |
| 29 | 523921830 | 8288566 | 30 | 1027813650 | 35512124 |
| … | … | … | … | … | … |
Пройдя через решетку с Фавном

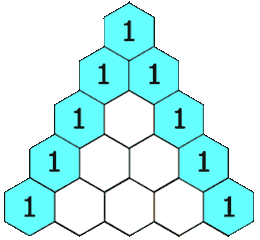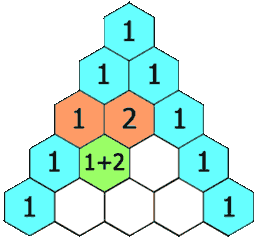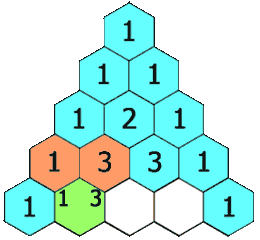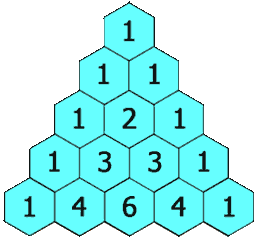
m и длинной со значением m. Следствием этой модели является то, что можно эффективно вычислить количество путей длиной 40 в 20x20 решетка с Фавном. Этот механизм встречного распространения аналогичен механическому способу вычисления биномиальных коэффициентов, предложенному Блезом Паскалем через треугольник Паскаля (в западном мире). Важно отметить, что это вычисление требует первого шага.
g = FaunusFactory.open('bin/titan-cassandra-input.properties')
t = System.currentTimeMillis()
// As of Faunus 0.3.1, the loop() construct is not supported
g.v(4).out.out.out.out.count() // 4-steps
t = System.currentTimeMillis() - t
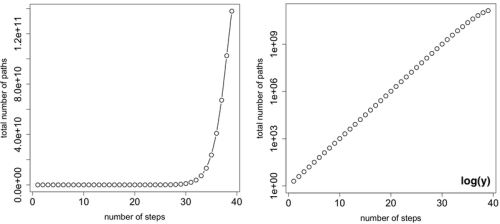
Количество путей длины n в 20x20 решетке изображено ниже в обеих y-линейной (слева) и y— логарифмической (справа) форме. Короче говоря, число путей растет экспоненциально с увеличением длины пути. Что интересно отметить в следующей таблице подсчета и времени выполнения Фаунуса, так это то, что Фаунус может вычислить общее количество уникальных путей длиной 40 в решетке за 10,53 минуты — 137 846 528 820.
| длина пути | количество путей | время прохождения (мс) | длина пути | количество путей | время прохождения (мс) |
|---|---|---|---|---|---|
| 1 | 2 | 32781 | 2 | 4 | 48071 |
| 3 | 8 | 63537 | 4 | 16 | 78575 |
| 5 | 32 | 94078 | 6 | 64 | 109246 |
| 7 | 128 | 124574 | 8 | 256 | 139850 |
| 9 | 512 | 156223 | 10 | 1024 | 171549 |
| 11 | 2048 | 186049 | 12 | 4096 | 201111 |
| 13 | 8192 | 218417 | 14 | 16384 | 232642 |
| 15 | 32768 | 248019 | 16 | 65536 | 263355 |
| 17 | 131072 | 278685 | 18 | 262144 | 296912 |
| 19 | 524288 | 308225 | 20 | 1048576 | 324440 |
| 21 | 2097150 | 340823 | 22 | 4194258 | 355349 |
| 23 | 8388054 | 371546 | 24 | 16772566 | 385755 |
| 25 | 33523880 | 402189 | 26 | 66941500 | 416868 |
| 27 | 133422540 | 433917 | 28 | 265069020 | 448150 |
| 29 | 523921830 | 462522 | 30 | 1027813650 | 478595 |
| 31 | 1995537270 | 493224 | 32 | 3821729910 | 508492 |
| 33 | 7191874140 | 524791 | 34 | 13237415400 | 539216 |
| 35 | 23690879520 | 556108 | 36 | 40885872720 | 568512 |
| 37 | 67156001220 | 586697 | 38 | 102501265020 | 601196 |
| 39 | 137846528820 | 617152 |
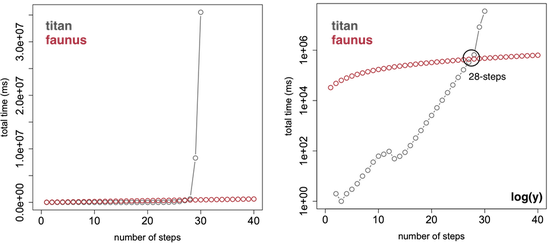
Время выполнения Титана растет в геометрической прогрессии, пропорционально количеству вычисленных путей. С другой стороны, время вычислений Фаунуса растет линейно при вычислении экспоненциального числа путей. На шаге 28 Фаунус выполняет подсчет путей быстрее, чем Титан. Это не означает, что Титан по своей природе менее эффективен при таких вычислениях, это просто функция перечислительной природы Гремлин / Титан, основанная на глубине, и противоположная природа Гремлин / Фаунус, ориентированная на ширину. Реализация движка Faunus Gremlin на Titan позволила бы Titan эффективно рассчитывать количество путей. Однако цель Faunus — служить глобальным пакетным процессором для Titan.
Вывод