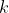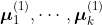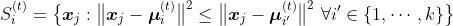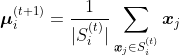В контексте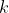 
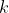
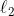
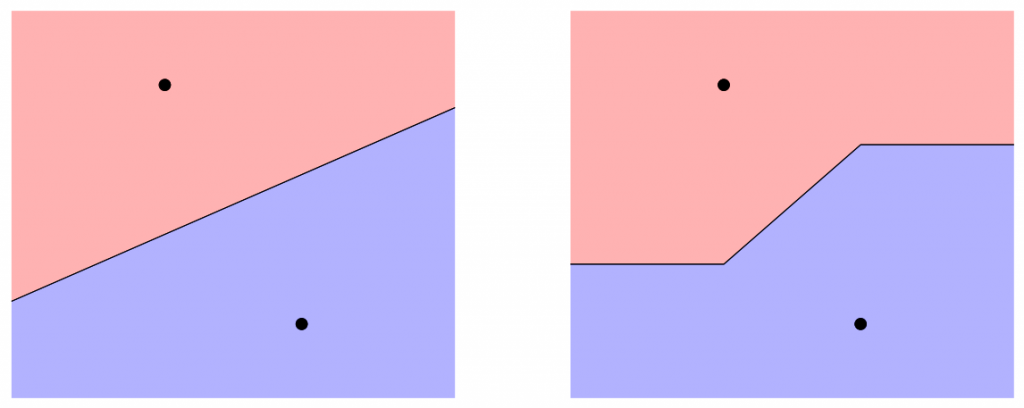
-means мы хотим разделить пространство наших наблюдений на классы. Каждое наблюдение принадлежит кластеру с ближайшим средним. Здесь «ближайший» означает некоторую норму, обычно 
(евклидову) норму.
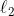
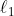
Рассмотрим случай, когда у нас есть 2 класса. Значит быть соответственно 2 черными точками. Если мы разделим на основе ближайшего среднего, с (евклидовой) нормой мы получим график слева, а с 
(манхэттенской) нормой — тот, что справа,
Точки в красной области ближе к среднему в верхней части, а точки в синей области ближе к среднему в нижней части. Здесь мы всегда будем использовать стандартную 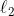(евклидову) норму. Обратите внимание, что график выше относится к диаграммам Вороного (или Вороного, от Вороний на украинском, или Вороно́й на русском) с 2 точками, 2 означает.
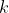
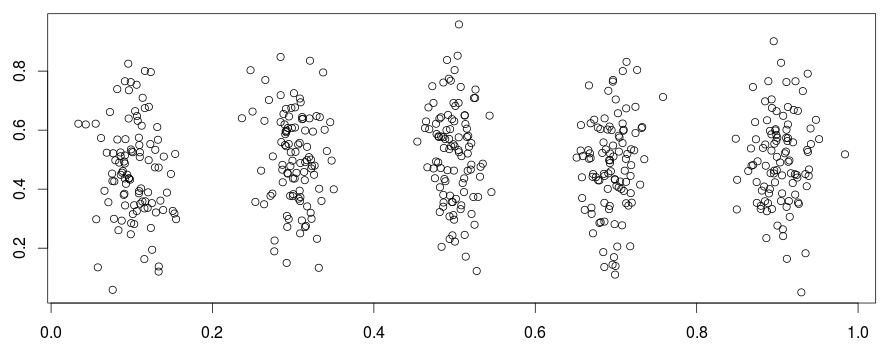
Чтобы проиллюстрировать алгоритм кластеризации -means (здесь алгоритм Ллойда ), рассмотрим следующий набор данных
set.seed(1) pts <- cbind(X=rnorm(500,rep(seq(1,9,by=2)/10,100),.022),Y=rnorm(500,.5,.15)) plot(pts)
Здесь у нас есть 5 групп. Итак, давайте запустим алгоритм 5-средних здесь.
- Мы рисуем случайным образом 5 точек в пространстве (начальные значения для средних),
- На шаге назначения мы присваиваем каждую точку ближайшему среднему
- На этапе обновления мы вычисляем новые центроиды кластеров
Чтобы визуализировать это, смотрите:
Код для получения кластеров:
kmeans(pts, centers=5, nstart = 1, algorithm = "Lloyd")
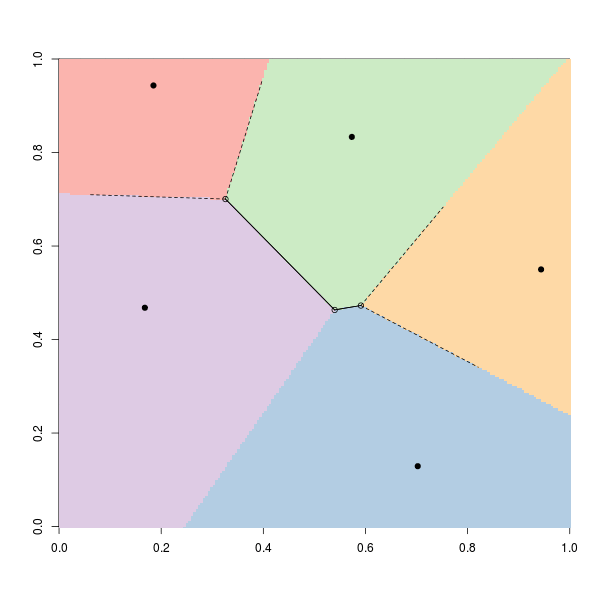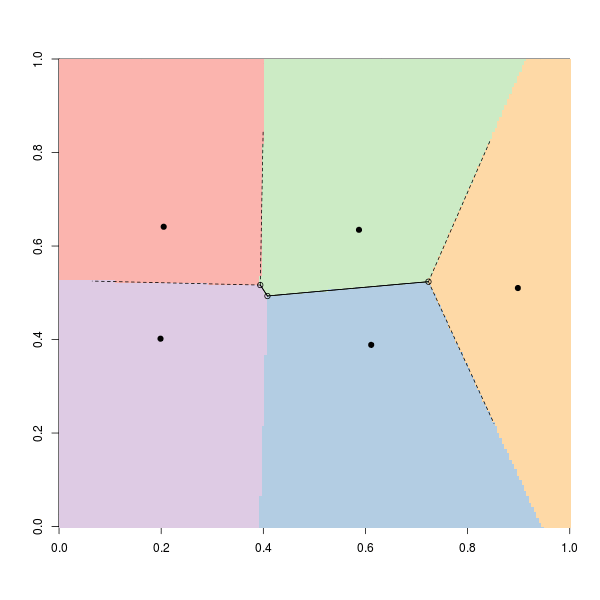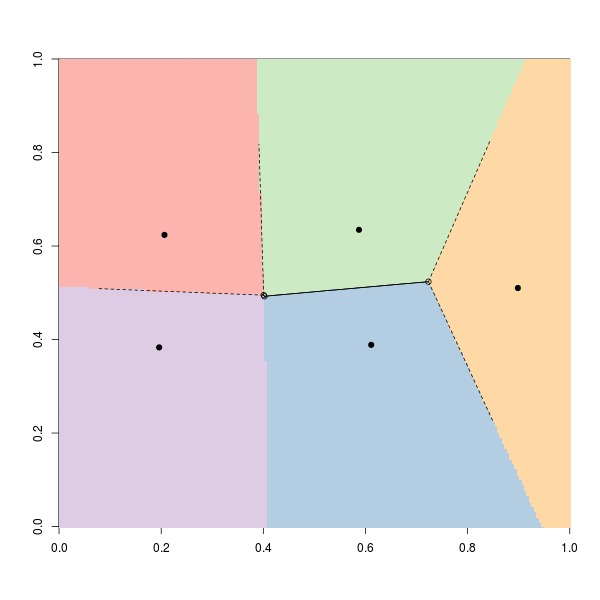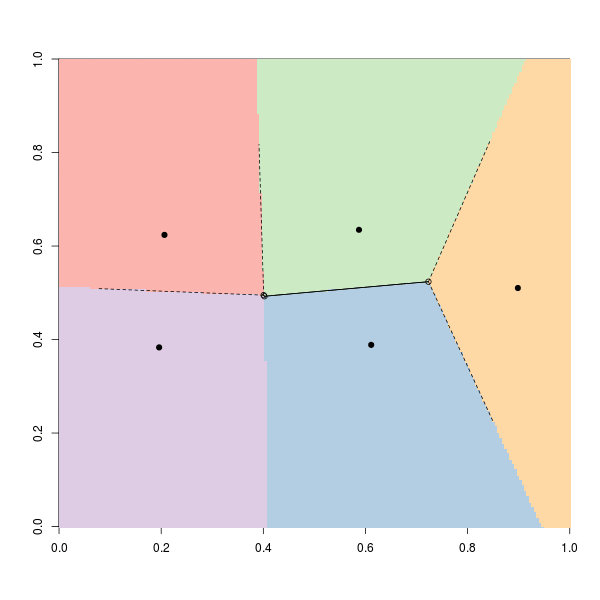
Заметим, что шаг назначения основан на вычислениях множеств Вороного. Это можно сделать в R используя:
library(tripack) V <- voronoi.mosaic(means[,1],means[,2]) P <- voronoi.polygons(V) points(V,pch=19) plot(V,add=TRUE)
Вот что мы можем визуализировать ниже:
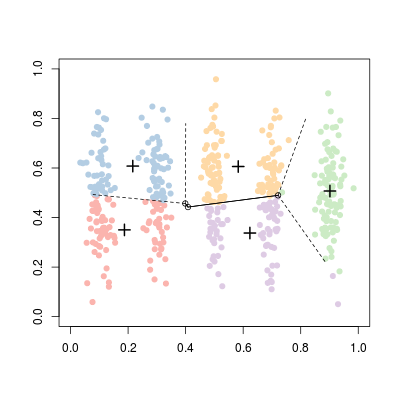
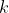
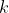
Код для визуализации средств и кластеров (или регионов) использует:
km1 <- kmeans(pts, centers=5, nstart = 1, algorithm = "Lloyd") library(tripack) library(RColorBrewer) CL5 <- brewer.pal(5, "Pastel1") V <- voronoi.mosaic(km1$centers[,1],km1$centers[,2]) P <- voronoi.polygons(V) plot(pts,pch=19,xlim=0:1,ylim=0:1,xlab="",ylab="",col=CL5[km1$cluster]) points(km1$centers[,1],km1$centers[,2],pch=3,cex=1.5,lwd=2) plot(V,add=TRUE)
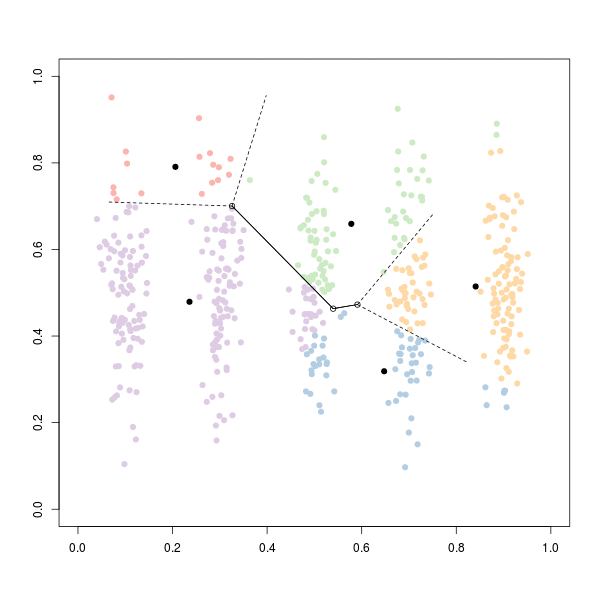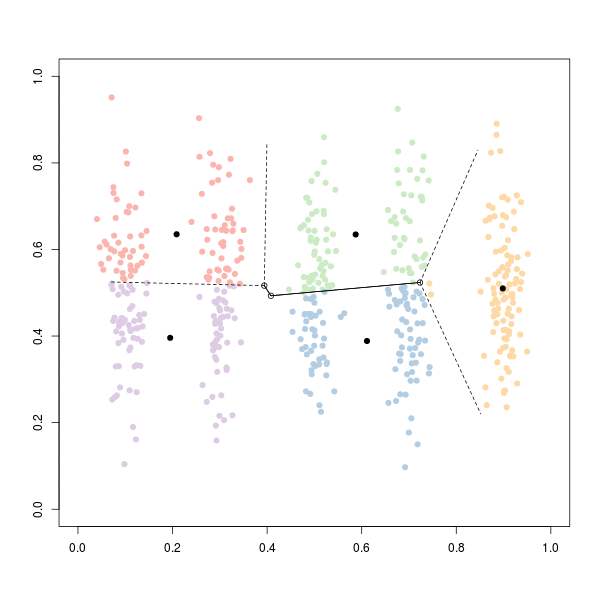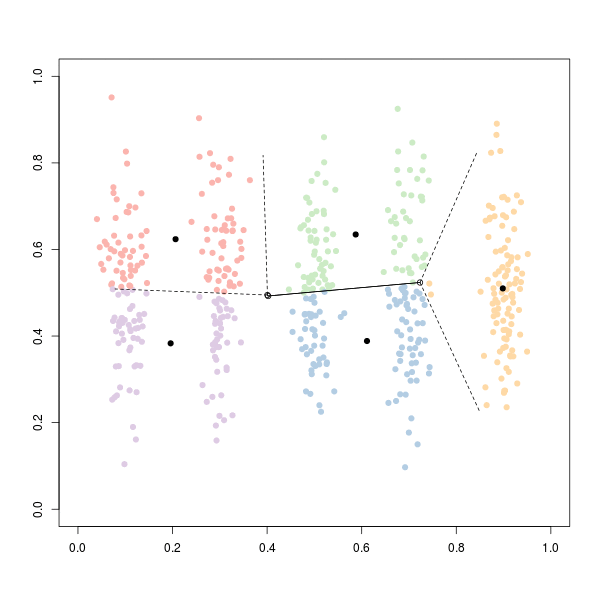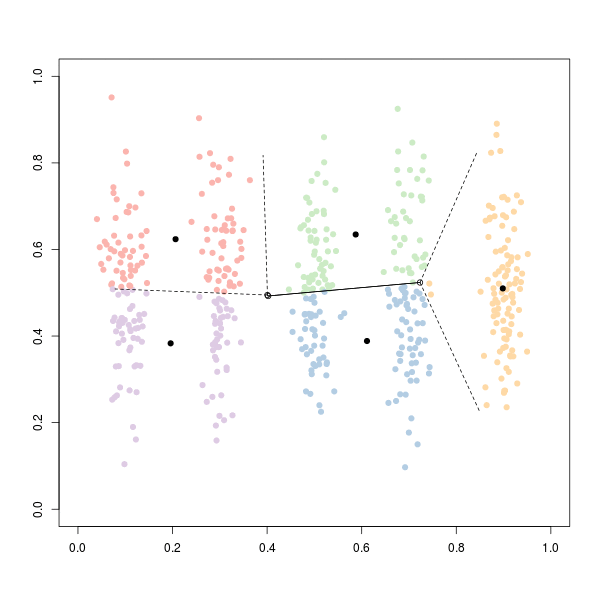
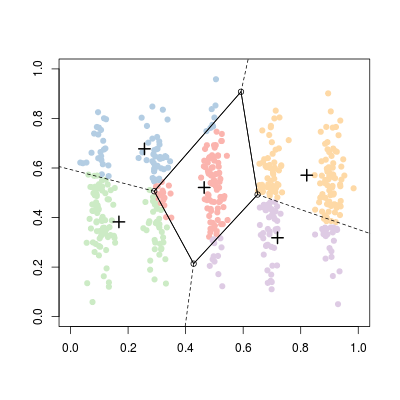
Здесь начальные точки нарисованы случайным образом. Если мы запустим его снова, мы можем получить:
Или же:
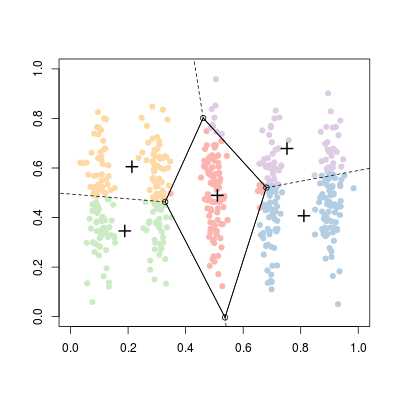
На этом наборе данных трудно получить кластер, который является пятью группами, которые мы можем фактически видеть. Если мы используем:
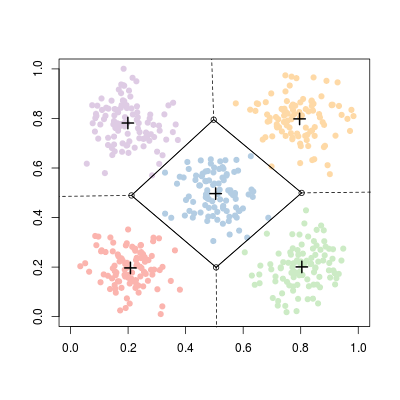
set.seed(1) A <- c(rep(.2,100),rep(.2,100),rep(.5,100),rep(.8,100),rep(.8,100)) B <- c(rep(.2,100),rep(.8,100),rep(.5,100),rep(.2,100),rep(.8,100)) pts <- cbind(X=rnorm(500,A,.075),Y=rnorm(500,B,.075))
мы обычно получаем что-то лучше.
Цвета получены из кластеров функции -means , но дополнительные линии получены с использованием в качестве выходных данных функций диаграмм Вороного .