Статьи

Использование Gremlin и транзакций для решения проблемы максимального потока

Октябрь 9, 2018

Т. Е. Харрис сформулировал проблему максимального потока следующим образом:

Рассмотрим железнодорожную сеть, соединяющую два города через ряд промежуточных городов, где каждому звену сети присвоен номер, представляющий его пропускную способность. Предполагая устойчивое состояние, найти максимальный поток из одного города в другой.

Еще в середине 1950-х годов военные США были заинтересованы в том, чтобы выяснить, какую пропускную способность советская железнодорожная сеть должна была перевезти из Западного Советского Союза в Восточную Европу. Это привело к проблеме максимального потока и алгоритму Форда-Фулкерсона для ее решения.

Если вы читали документацию к плагину Neo4j Gremlin, вы наверняка помните, что в нем есть раздел, посвященный алгоритмам Flow с Gremlin . Давайте добавим пару вещей и воплотим этот пример в жизнь.

 

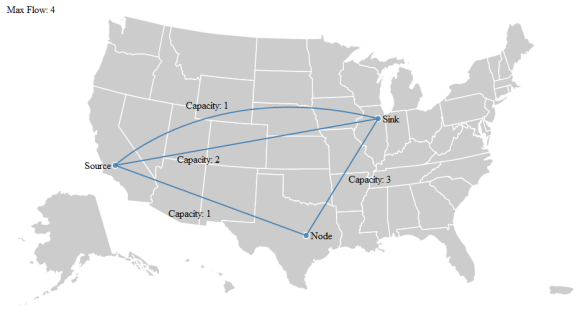
Мы собираемся смоделировать простую железнодорожную систему, которая должна перевозить грузы из Калифорнии в Иллинойс. Существует несколько прямых маршрутов, и дополнительно маршрут, проходящий через Техас. Первый шаг — создать наш график:

def create_graph
  neo = Neography::Rest.new
  graph_exists = neo.get_node_properties(1)
  return if graph_exists && graph_exists['name']

  states = [{:name => "California", :coordinates => [-119.355165,35.458606]},
            {:name => "Illinois",   :coordinates => [ -88.380238,41.278216]},
            {:name => "Texas",      :coordinates => [ -97.388631,30.943149]}]

  commands = states.map{ |n| [:create_node, n]}
  
  states.each_index.map do  |n| 
    commands << [:add_node_to_index, "states_index", "name", states[n][:name], "{#{n}}"] 
  end
  
  commands << [:create_relationship, "connected", "{#{0}}", "{#{1}}", {:capacity => 1}]    
  commands << [:create_relationship, "connected", "{#{0}}", "{#{1}}", {:capacity => 2}]
  commands << [:create_relationship, "connected", "{#{0}}", "{#{2}}", {:capacity => 1}]
  commands << [:create_relationship, "connected", "{#{2}}", "{#{1}}", {:capacity => 3}]

  batch_result = neo.batch *commands
end

 

Вы видели, как я делал это уже несколько раз, поэтому я не буду тратить на это слишком много времени. Просто обратите внимание, что мы добавляем имена состояний в индекс и используем команду BEST REST, чтобы создать все сразу. Мы напишем наш метод max_flow следующим образом:

def max_flow
  neo = Neography::Rest.new
  neo.execute_script("source = g.idx('states_index')[[name:'California']].iterator().next(); 
                      sink = g.idx('states_index')[[name:'Illinois']].iterator().next();
                      
                      max_flow = 0;
                      g.setMaxBufferSize(0);
                      g.startTransaction();
                       
                      source.outE.inV.loop(2){
                        !it.object.equals(sink)}.
                      paths.each{
                        flow = it.capacity.min();
                        max_flow += flow;
                        it.findAll{
                          it.capacity}.each{
                            it.capacity -= flow}
                            };
                      g.stopTransaction(TransactionalGraph.Conclusion.FAILURE); 
                            
                      max_flow;")
end

Let’s take a closer look at a few things. We use the index to look up our source (start) and sink (end) nodes, and use iterator().next() to get the first node from the Gremlin Groovy Pipeline returned by the index lookup. We also create a variable max_flow where our answer will go.

source = g.idx('states_index')[[name:'California']].iterator().next(); 
sink = g.idx('states_index')[[name:'Illinois']].iterator().next();
max_flow = 0;

We then set the transaction mode to manual by setting the MaxBufferSize to zero and start a new transaction. I’ll explain why in a minute.

g.setMaxBufferSize(0);
g.startTransaction();

 

From our source, we go to a neighboring node looping these two outE.inV steps until we reach the sink node.

source.outE.inV.loop(2){
!it.object.equals(sink)}.

 For each path we find the lowest capacity along the edges we traversed using the min() function and add it to the max_flow variable we created earlier.

paths.each{
  flow = it.capacity.min();
  max_flow += flow;

 Then we subtract the flow from the capacity property of each of the edges in our path. Take note we are actually altering data in this step. 

it.findAll{
  it.capacity}.each{
    it.capacity -= flow}
};

At the end we return max_flow which has the answer to our question.

max_flow;

 If you tried to run this method again, or tried to run a similar method using different sinks and sources that traveled over these nodes you’ll have a problem. The capacities were modified and will most likely be zero or show the residual capacity of the transportation network we built.

So to prevent this we stop the transaction with a Failure. The changes we made to capacity are not committed and the graph stays the way it was.

g.stopTransaction(TransactionalGraph.Conclusion.FAILURE);

 

We can visualize this example using D3.js and its Geo Path projections:

As usual, all code is available on github. The max flow and related problems manifest in many ways. Water or sewage through underground pipes, passengers on a subway system, data through a network (the internet is just a series of tubes!), roads and highway planning, airline routes, even determining which sports teams have been eliminated from the playoffs.

Source: http://maxdemarzi.com/2012/02/21/max-flow-with-gremlin-and-transactions/

34
Share: