Алгоритмы ранжирования графа предназначены для отображения сложной графической структуры на числовой вектор. Для данного алгоритма единственное числовое значение в результирующем векторе соответствует значению конкретной вершины в графе. В коде предыдущие структуры определены ниже с использованием Groovy и Blueprints .
def g = new Neo4jGraph('/tmp/neo4j'); // the graph
def m = new HashMap<Vertex,Double>(); // the rank vector
Ранжирование графа может быть разбито на две под-концепции: глобальные и локальные ранги. Это различие раскрывается в этом посте.
Глобальные метрики ранга
Многие из популярных алгоритмов ранжирования графов являются глобальными. Хороший список прачечной представлен на центральной странице Википедии . Стандарты учебника включают алгоритмы на основе собственных векторов (например, PageRank, центральность собственных векторов) и алгоритмы на основе геодезических (например, между близости, центральности близости). Общим для этих алгоритмов является то, что они ранжируют все вершины графа относительно всех вершин графа. Таким образом, весь граф анализируется для определения оценки какой-либо одной вершины, где возвращаемый вектор ранга представляет собой размер общего числа вершин в графе. Эта идея выражена в Groovy, Blueprints и Gremlin ниже.
public Map<Vertex,Double> global(Graph g) {
g.V.each{ ... }
}
def g = new Neo4jGraph('/tmp/neo4j');
assert global(g).size() == g.V.count();
Note that the global rank method only takes a single graph argument. This is because the graph has all the information needed to calculate the ranking–all the vertices can be derived from the graph. However, nothing prevents a subset of the vertices being ranked relative to some subset of vertices. Such algorithms are called local rank metrics and are discussed next.
Local Rank Metrics
A key article articulating the concept of local rank is Algorithms for Estimating Relative Importance in Networks by Scott White and Padhraic Smyth. In this article, the authors chose to explore the question:
“Which entities are most important in the [graph] relative to a particular individual or set of individuals?
The codified structure of this statement is provided below.
public Map<Vertex,Double> local(Set<Vertex> roots) {
roots.each{ ... }
}
def g = new Neo4jGraph('/tmp/neo4j');
def roots = g.V[0..10]; // some subset of V
assert local(roots).size() <= g.V.count();
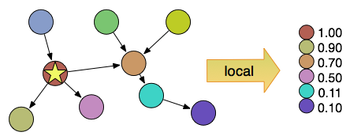
With local rank metrics, a set of root vertices serves as the source of the ranking. All vertices in the graph (or some subset thereof as not all vertices may be reachable or close enough to be touched) are then ranked relative to this root set. When this root set contains only one vertex, this is known as an ego-rank. When this root set contains all vertices, this is know as a global rank. Thus, the concept of local rank is fuzzy.
An interesting class of local rank metrics are the recommendation metics. For example, a website might have many users and many items. Users may like items. When a particular user is logged in, a recommendation can occur which ranks the items in the graph relative to the user. Given that the recommendation is relative to a single user vertex, the algorithm is an ego-rank. Basic collaborative filtering is an example of a local, ego-rank metric. The Gremlin snippet below ranks/recommends items relative to user vertex 1 using basic collaborative filtering.
def m = new HashMap<Vertex,Double>()
g.v(1).outE('likes').inV.inE('likes').outV.outE('likes').inV.groupCount(m);
In English, the code says get vertex 1 from the graph, determine which items user 1 likes, determine which users also like those liked items, determine which items thoseusers like, then finally, rank those items by how many times they are traversed. Thus, a ranking is returned that is rooted at vertex 1.
There is also the concept of local centrality. That is, determine which vertices are most central to some root set of vertices. The classic algorithm of this nature isspreading activation. With spreading activation, a set of root vertices is “stimulated with energy” and that energy emanates from those roots as it diffuses over the edges of the graph. The vertices with the most energy flow over some number of steps are considered the most central relative to the root set. A theoretically interesting instance of the spreading activation algorithm is PageRank Priors which is discussed in the White and Smyth article previous mentioned.
Conclusion
Most of the discussion on graph ranking is focused on global rank metrics. However, in many situations, local metrics are both more useful and more efficient. They are more useful in situations such as personalization. They are more efficient in that they do not require a full traversal of the graph and are usually completed in only a few hops out from the root set.
If you use Gremlin and your code has the form
g.V.something.groupCount(m).loop{ }
then you are doing a global rank algorithm. If your Gremlin code has the form
g.v(1).something.groupCount(m).loop{ }
then you are doing a local rank algorithm. Both types of ranking algorithms have their place and are generally useful for distilling a complex structure into a ranked list of numbers. In other words, both are helpful at making sense of the graph.
References
White, S., Smyth, P., Algorithms for Estimating Relative Importance in Networks, Special Interest Group on Knowledge Discovery and Data Mining (SIGKDD), August 24–27, 2003.