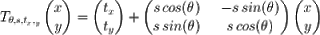Часто в задачах Computer Vision у нас есть модель интересной формы, и мы хотим знать, совпадает ли эта модель с целевой формой, найденной путем анализа краев изображения. Форма цели никогда не идентична имеющейся у нас модели, потому что она может быть представлением модели в другой позе или может лишь частично соответствовать нашей модели, поэтому мы должны найти правильное преобразование модели, чтобы соответствовать цель. В этом посте мы увидим, как найти модель, ближайшую к целевой фигуре, используя функцию fmin, предоставляемую Scipy.
Мы можем представить форму с помощью матрицы, как показано ниже:
где каждая пара (x i , y i ) является «ориентиром» точки фигуры, и мы можем преобразовать каждую общую точку (x, y), используя эту функцию:
В этом преобразовании мы имеем, что θ — угол поворота, t x и t y — сдвиг по оси x и y соответственно, а s — коэффициент масштабирования. Применяя это преобразование к каждой точке формы, описанной X, мы получаем новую форму, которая является преобразованием исходной формы в соответствии с параметрами, используемыми в T. Учитывая матрицу, как определено выше, следующая функция Python способна применить преобразование к каждой точке формы, представленной матрицей:
import numpy as np
import pylab as pl
from scipy.optimize import fmin
def transform(X,theta,tx=0,ty=0,s=1):""" Performs scaling, rotation and translation
on the set of points in the matrix X
Input:
X, points (each row have to be a point [x, y])
theta, rotation angle (in radiants)
tx, translation along x
ty, translation along y
s, scaling coefficient
Return:
Y, transformed set of points
"""
a = math.cos(theta)
b = math.sin(theta)
R = np.mat([[a*s,-b*s],[b*s, a*s]])
Y = R*X # rotation and scaling
Y[0,:]= Y[0,:]+tx # translation
Y[1,:]= Y[1,:]+ty
return Y
Теперь мы хотим найти лучшую позу (перемещение, масштаб и вращение), чтобы сопоставить форму модели X с целевой формой Y. Мы можем решить эту проблему, сводя к минимуму сумму квадратных расстояний между точками X и Y, а это значит, что мы хотим найти
где T ‘- это функция, которая применяет T ко всем точкам входной фигуры. Эта задача оказывается довольно простой, используя функцию fmin, предоставляемую Scipy:
def error_fun(p,X,Y):""" cost function to minimize """return np.linalg.norm(transform(X,p[0],p[1],p[2],p[3])-Y)def match(X,Y,p0):""" Match the model X with the shape Y
returns the set of parameters to transform
X into Y and a set of partial solutions.
"""
p_opt = fmin(error_fun, p0, args=(X,Y),retall=True)return p_opt[0],p_opt[1]# optimal solutions, other solutions
В приведенном выше коде мы определили функцию стоимости, которая измеряет, насколько близки две фигуры, и другую функцию, которая минимизирует разницу между двумя фигурами и возвращает параметры преобразования. Теперь мы можем попытаться сопоставить форму трилистника, начиная с одного из ее преобразований, используя функции, определенные выше:
# generating a shape to match t = np.linspace(0,2*np.pi,50) x =2*np.cos(t)-.5*np.cos(4*t ) y =2*np.sin(t)-.5*np.sin(4*t ) A = np.array([x,y])# model shape# transformation parameters p =[-np.pi/2,.5,.8,1.5]# theta,tx,ty,sAr= transform(A,p[0],p[1],p[2],p[3])# target shape p0 = np.random.rand(4)# random starting parameters p_opt, allsol = match(A,Ar,p0)# matching
Интересно визуализировать ошибку на каждой итерации:
pl.plot([error_fun(s,A,Ar)for s in allsol]) pl.show()
и значение параметров преобразования на каждой итерации:
pl.plot(allsol) pl.show()
Из приведенных выше графиков видно, что процесс минимизации нашел свое решение после 150 итераций. Действительно, после 150 итераций ошибка становится очень близкой к нулю, и параметры практически не изменяются. Теперь мы можем визуализировать процесс минимизации, отображая некоторые решения, чтобы сравнить их с целевой формой:
def plot_transform(A,p):Afound= transform(A,p[0],p[1],p[2],p[3])
pl.plot(Afound[0,:].T,Afound[1,:].T,'-')for k,i in enumerate(range(0,len(allsol),len(allsol)/15)):
pl.subplot(4,4,k+1)
pl.plot(Ar[0,:].T,Ar[1,:].T,'--',linewidth=2)# target shape
plot_transform(A,allsol[i])
pl.axis('equal')
pl.show()
На графике выше мы видим, что исходные решения (зеленые) очень отличаются от формы, которую мы пытаемся сопоставить (пунктирные синие), и что в процессе минимизации они приближаются к целевой фигуре, пока не подойдут это полностью. В приведенном выше примере мы использовали две фигуры одинаковой формы. Давайте посмотрим, что произойдет, когда у нас будет начальная форма, которая отличается от целевой модели:
t = np.linspace(0,2*np.pi,50) x = np.cos(t) y = np.sin(t)Ac= np.array([x,y])# the circle (model shape) p0 = np.random.rand(4)# random starting parameters# the target shape is the trifoil again p_opt, allsol = match(Ac,Ar,p0)# matching
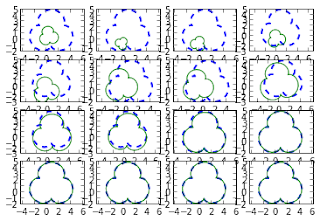
В приведенном выше примере мы использовали круг в качестве модельной фигуры и трилистник в качестве целевой фигуры. Давайте посмотрим, что произошло в процессе минимизации:
for k,i in enumerate(range(0,len(allsol),len(allsol)/15)):
pl.subplot(4,4,k+1)
pl.plot(Ar[0,:].T,Ar[1,:].T,'--',linewidth=2)# target shape
plot_transform(Ac,allsol[i])
pl.axis('equal')
pl.show()
В этом случае, когда форма модели не может полностью соответствовать целевой форме, мы видим, что процесс минимизации может найти круг, который находится ближе к трилистнику.