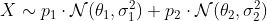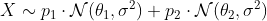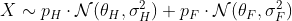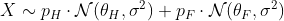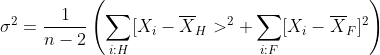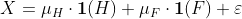Недавно в классе ACT2040 (по страхованию, не связанному со страхованием жизни) мы обсудили разницу между наблюдаемой и ненаблюдаемой неоднородностью в нормировании (с экономической точки зрения). Чтобы проиллюстрировать этот момент (позже мы потратим больше времени на обсуждение наблюдаемых и ненаблюдаемых факторов риска), мы рассмотрели следующий простой пример. Позвольте
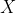 обозначить рост человека. Рассмотрим следующий набор данных:
обозначить рост человека. Рассмотрим следующий набор данных:> Davis=read.table( + "http://socserv.socsci.mcmaster.ca/jfox/Books/Applied-Regression-2E/datasets/Davis
В наборе данных есть небольшая опечатка, поэтому давайте внесем здесь ручные изменения.
> Davis[12,c(2,3)]=Davis[12,c(3,2)]
Здесь переменная интереса — рост данного человека:
> X=Davis$height
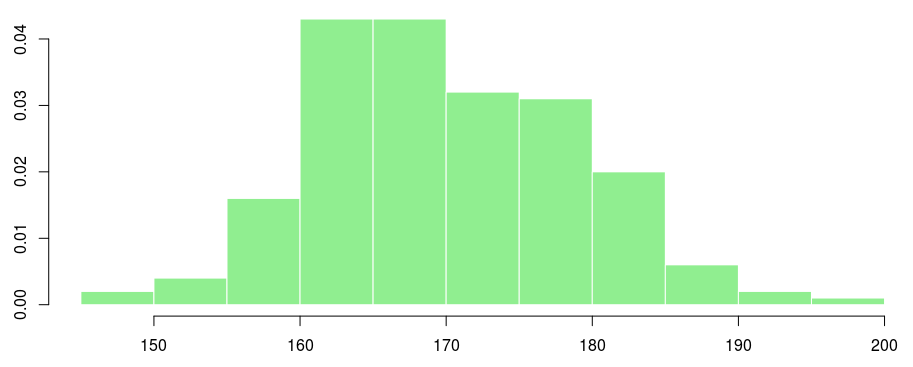
Если мы посмотрим на гистограмму, мы имеем:
> hist(X,col="light green", border="white",proba=TRUE,xlab="",main="")
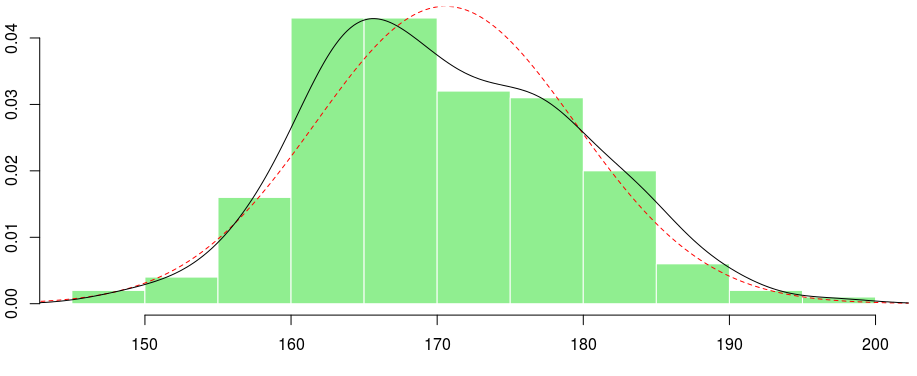
Можем ли мы предположить, что у нас есть распределение Гаусса?
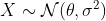
> (param <- fitdistr(X,"normal")$estimate) > f1 <- function(x) dnorm(x,param[1],param[2]) > x=seq(100,210,by=.2) > lines(x,f1(x),lty=2,col="red") > lines(density(X))
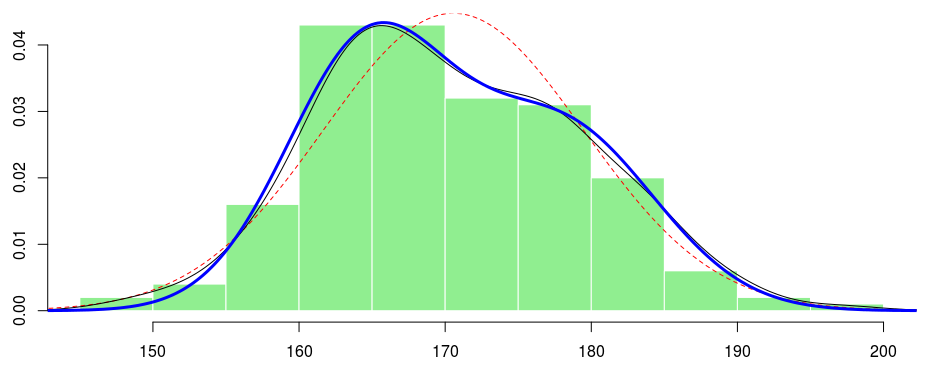
Если вы посмотрите на эту черную линию, вы можете подумать о смеси, что-то вроде:
(с использованием стандартных обозначений смеси). Смеси получаются, когда мы имеем ненаблюдаемый фактор неоднородности : с вероятностью 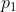
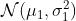
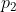
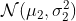
> library(mixtools) > mix <- normalmixEM(X) number of iterations= 335 > (param12 <- c(mix$lambda[1],mix$mu,mix$sigma)) [1] 0.4002202 178.4997298 165.2703616 6.3561363 5.9460023
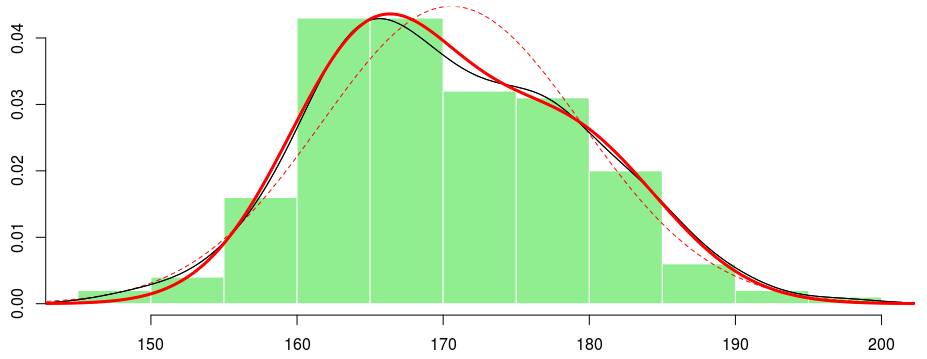
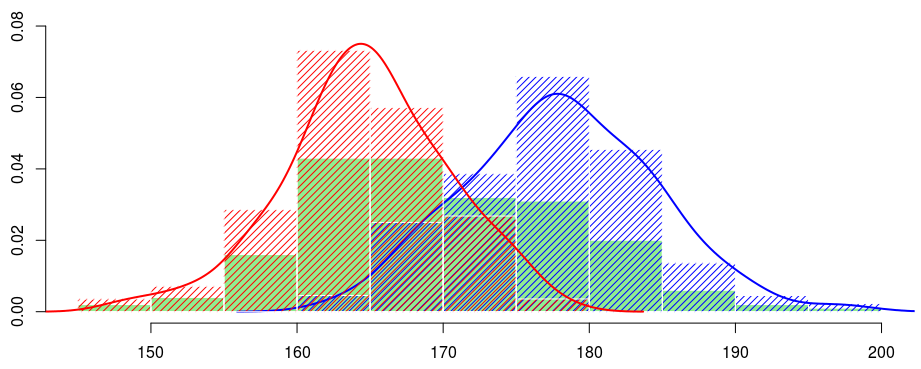
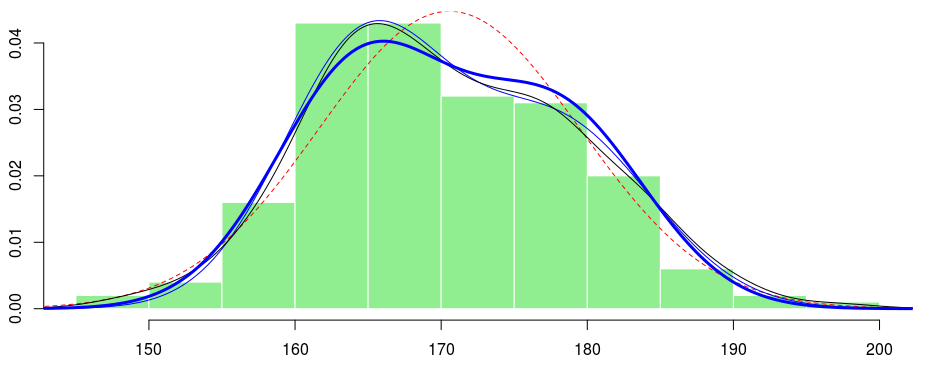
Если мы построим эту смесь двух гауссовых распределений, мы получим:
> f2 <- function(x){ param12[1]*dnorm(x,param12[2],param12[4])
+ (1-param12[1])*dnorm(x,param12[3],param12[5]) }
> lines(x,f2(x),lwd=2, col="red") lines(density(X))
Неплохо. На самом деле, мы можем попытаться максимизировать вероятность с помощью наших собственных кодов:
> logdf <- function(x,parameter){
+ p <- parameter[1]
+ m1 <- parameter[2]
+ s1 <- parameter[4]
+ m2 <- parameter[3]
+ s2 <- parameter[5]
+ return(log(p*dnorm(x,m1,s1)+(1-p)*dnorm(x,m2,s2)))
+ }
> logL <- function(parameter) -sum(logdf(X,parameter))
> Amat <- matrix(c(1,-1,0,0,0,0,
+ 0,0,0,0,1,0,0,0,0,0,0,0,0,1), 4, 5)
> bvec <- c(0,-1,0,0)
> constrOptim(c(.5,160,180,10,10), logL, NULL, ui = Amat, ci = bvec)$par
[1] 0.5996263 165.2690084 178.4991624 5.9447675 6.3564746
Здесь мы включаем некоторые ограничения, чтобы гарантировать, что вероятность принадлежит единичному интервалу, и что параметры отклонения остаются положительными. Обратите внимание, что у нас есть что-то близкое к предыдущему выводу.
Давайте попробуем что-нибудь более сложное сейчас. Что если предположить, что базовые распределения имеют одинаковую дисперсию, а именно:
В этом случае мы должны использовать предыдущий код и внести небольшие изменения:
> logdf <- function(x,parameter){
+ p <- parameter[1]
+ m1 <- parameter[2]
+ s1 <- parameter[4]
+ m2 <- parameter[3]
+ s2 <- parameter[4]
+ return(log(p*dnorm(x,m1,s1)+(1-p)*dnorm(x,m2,s2)))
+ }
> logL <- function(parameter) -sum(logdf(X,parameter))
> Amat <- matrix(c(1,-1,0,0,0,0,0,0,0,0,0,1), 3, 4)
> bvec <- c(0,-1,0)
> (param12c= constrOptim(c(.5,160,180,10), logL, NULL, ui = Amat, ci = bvec)$par)
[1] 0.6319105 165.6142824 179.0623954 6.1072614
Это то, что мы можем сделать, если не можем наблюдать фактор неоднородности. Но подождите … у нас на самом деле есть некоторая информация в наборе данных. Например, у нас есть пол человека. Теперь, если мы посмотрим на гистограммы роста по полу и основанную на ядре оценку плотности роста по полу, мы получим
Итак, это выглядит как рост для мужчины, а рост для женщины разные. Возможно, мы можем использовать эту переменную, которая действительно наблюдалась, чтобы объяснить неоднородность в нашей выборке. Формально идея состоит в том, чтобы рассмотреть смесь с наблюдаемым фактором неоднородности : пол.
Теперь у нас есть интерпретация того, что мы раньше называли классом [1] и [2]: мужской и женский. И здесь, оценка параметров довольно проста,
> (pM <- mean(sex=="M"))
[1] 0.44
> (paramF <- fitdistr(X[sex=="F"],"normal")$estimate)
mean sd
164.714286 5.633808
> (paramM <- fitdistr(X[sex=="M"],"normal")$estimate)
mean sd
178.011364 6.404001
И если мы строим плотность, мы имеем
> f4 <- function(x) pM*dnorm(x,paramM[1],paramM[2])+(1-pM)*dnorm(x,paramF[1],paramF[2]) > lines(x,f4(x),lwd=3,col="blue")
Что, если мы снова примем одинаковую дисперсию? А именно модель становится:
Тогда естественной идеей для получения оценки дисперсии, основанной на предыдущих вычислениях, является использование:
Код здесь:
> s=sqrt((sum((height[sex=="M"]-paramM[1])^2)+sum((height[sex=="F"]-paramF[1])^2))/(nrow(Davis)-2)) > s [1] 6.015068
и снова, можно построить соответствующую плотность,
> f5 <- function(x) pM*dnorm(x,paramM[1],s)+(1-pM)*dnorm(x,paramF[1],s) > lines(x,f5(x),lwd=3,col="blue")
Теперь, если мы немного подумаем о том, что мы только что сделали, это просто линейная регрессия на фактор, пол человека:
где 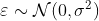
> summary(lm(height~sex,data=Davis))
Call:
lm(formula = height ~ sex, data = Davis)
Residuals:
Min 1Q Median 3Q Max
-16.7143 -3.7143 -0.0114 4.2857 18.9886
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 164.7143 0.5684 289.80 <2e-16 ***
sexM 13.2971 0.8569 15.52 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.015 on 198 degrees of freedom
Multiple R-squared: 0.5488, Adjusted R-squared: 0.5465
F-statistic: 240.8 on 1 and 198 DF, p-value: < 2.2e-16
И мы получаем те же оценки для средних и дисперсии, что и ранее. Итак, как недавно упоминалось в классе, если у вас есть ненаблюдаемый фактор неоднородности, мы можем использовать смешанную модель для соответствия распределению, но если вы можете получить прокси этого фактора, который можно наблюдать, вы можете запустить регрессию. Но большую часть времени эта наблюдаемая переменная является просто прокси ненаблюдаемой …