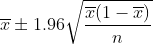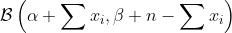Статьи

Доверие против доверительных интервалов

Апрель 7, 2018

Завтра, в заключительной лекции по курсу « Математическая статистика» , я попытаюсь проиллюстрировать — используя симуляции Монте-Карло — разницу между классической статистикой и байесовским подходом.

(Простой) способ, которым я вижу это следующее

  • для частых людей вероятность — это мера частоты повторяющихся событий, поэтому интерпретация заключается в том, что параметры являются фиксированными (но неизвестными), а данные являются случайными
  • для байесовской вероятности — это мера степени достоверности значений, поэтому интерпретация заключается в том, что параметры случайны, а данные фиксированы

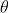
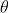
Или процитировать частоту и байесианство: учебник для начинающих , основанный на Python , байесовский статистик сказал бы: «учитывая наши наблюдаемые данные, существует 95% вероятность того, что истинное значение  http://latex.codecogs.com/gif.latex?\thetaпопадает в достоверный регион», в то время как статистик-распространитель скажет «есть 95% вероятности того, что когда я вычислю доверительный интервал из данных такого рода, истинное значение  http://latex.codecogs.com/gif.latex?\thetaпопадет в него ».

Чтобы лучше понять эти цитаты, рассмотрим простую проблему, связанную с испытаниями Бернулли, со страховыми претензиями. Мы хотим вывести некоторый доверительный интервал для вероятности претендовать на убыток. Было 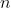http://latex.codecogs.com/gif.latex?n1047 политик. И 159 претензий.

Рассмотрим стандартный (частый) доверительный интервал. Что это значит

http://latex.codecogs.com/gif.latex?\overline{x}\pm%201.96%20\sqrt{\frac{\overline{x}(1-\overline{x})}{n}}

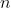
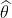
это (асимптотический) 95% доверительный интервал? То, как я это вижу, очень просто. Давайте сгенерируем несколько выборок по размеру http://latex.codecogs.com/gif.latex?nс той же вероятностью, что и эмпирическая, т. Е. http://latex.codecogs.com/gif.latex?\widehat{\theta}(Что означает «из данных такого рода»). Для каждого образца вычислите доверительный интервал с приведенным выше соотношением. Это 95% доверительный интервал, потому что в 95% сценариев эмпирическое значение лежит в доверительном интервале. С вычислительной точки зрения это следующая идея:

> xbar <- 159
> n <- 1047
> ns <- 100
> M=matrix(rbinom(n*ns,size=1,prob=xbar/n),nrow=n)

Я генерирую 100 образцов размера 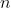http://latex.codecogs.com/gif.latex?n. Для каждого образца я вычисляю среднее значение и доверительный интервал из предыдущего отношения:

> fIC=function(x) mean(x)+c(-1,1)*1.96*sqrt(mean(x)*(1-mean(x)))/sqrt(n)
> IC=t(apply(M,2,fIC))
> MN=apply(M,2,mean)

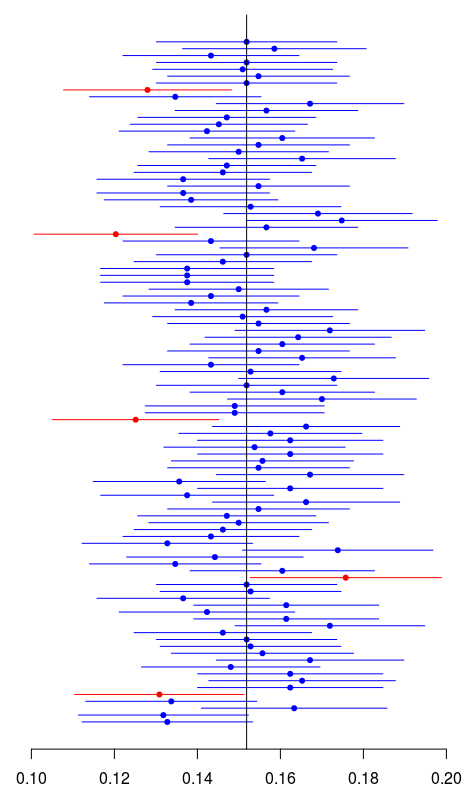
Затем мы строим все эти доверительные интервалы. Красным цветом, если они не содержат эмпирического значения:

> k=(xbar/n<IC[,1])|(xbar/n>IC[,2])
> plot(MN,1:ns,xlim=range(IC),axes=FALSE,
+ xlab="",ylab="",pch=19,cex=.7,
+ col=c("blue","red")[1+k])
> axis(1)
> segments(IC[,1],1:ns,IC[,2],1:
+ ns,col=c("blue","red")[1+k])
> abline(v=xbar/n)

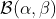
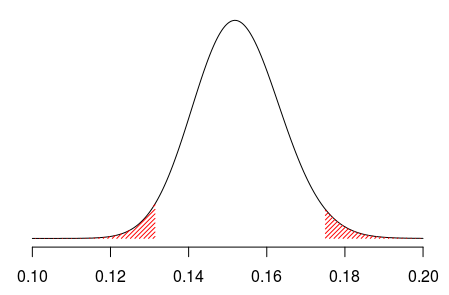
А как насчет байесовского вероятного интервала? Предположим, что предыдущее распределение вероятности претендовать на потерю имеет http://latex.codecogs.com/gif.latex?\mathcal{B}(\alpha,\beta)распределение. В ходе курса мы видели, что, поскольку бета-распределение является сопряженным с Бернулли, последующее распределение также будет бета-распределением. Точнее:

http://latex.codecogs.com/gif.latex?\mathcal{B}\left(\alpha+\sum%20x_i,\beta+n-\sum%20x_i\right)

На основе этого свойства доверительный интервал основан на квантилях этого (апостериорного) распределения

> u=seq(.1,.2,length=501)
> v=dbeta(u,1+xbar,1+n-xbar)
> plot(u,v,axes=FALSE,type="l")
> I=u<qbeta(.025,1+xbar,1+n-xbar)
> polygon(c(u[I],rev(u[I])),c(v[I],
+ rep(0,sum(I))),col="red",density=30,border=NA)
> I=u>qbeta(.975,1+xbar,1+n-xbar)
> polygon(c(u[I],rev(u[I])),c(v[I],
+ rep(0,sum(I))),col="red",density=30,border=NA)
> axis(1)

Что это значит здесь, что у нас есть 95% вероятный интервал? Что ж, на этот раз мы рисуем не с использованием эмпирического среднего, а с некоторой возможной вероятностью, основанной на этом последнем распределении (с учетом наблюдений):

> pk <- rbeta(ns,1+xbar,1+n-xbar)

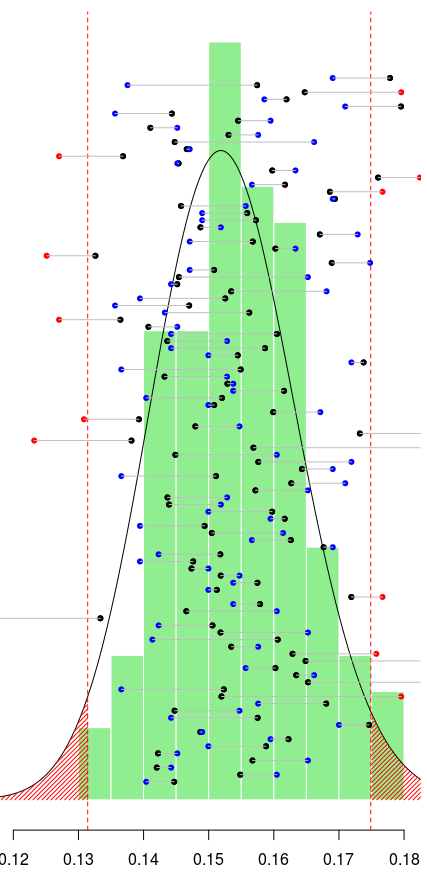
Зеленым цветом ниже мы можем визуализировать гистограмму этих значений:

> hist(pk,prob=TRUE,col="light green",
+ border="white",axes=FALSE,
+ main="",xlab="",ylab="",lwd=3,xlim=c(.12,.18))

И здесь снова давайте сгенерируем выборки и вычислим эмпирические вероятности:

> M=matrix(rbinom(n*ns,size=1,prob=rep(pk,
+ each=n)),nrow=n)
> MN=apply(M,2,mean)

Здесь есть 95% вероятность того, что эти эмпирические средние значения лежат в вероятном интервале, определяемом с помощью квантилей апостериорного распределения. На самом деле мы можем визуализировать все эти средства: черным цветом обозначено среднее значение, используемое для генерации выборки, а затем синим или красным цветом средние значения, полученные для этих имитированных выборок:

> abline(v=qbeta(c(.025,.975),1+xbar,1+
+ n-xbar),col="red",lty=2)
> points(pk,seq(1,40,length=ns),pch=19,cex=.7)
> k=(MN<qbeta(.025,1+xbar,1+n-xbar))|
+ (MN>qbeta(.975,1+xbar,1+n-xbar))
> points(MN,seq(1,40,length=ns),
+ pch=19,cex=.7,col=c("blue","red")[1+k])
> segments(MN,seq(1,40,length=ns),
+ pk,seq(1,40,length=ns),col="grey")

Более подробная информация и пример байесовской статистики, увиденной глазами (возможно) не байесовской статистики на моих слайдах из моего выступления в Лондоне прошлым летом:



39
Share: