В актуарной науке и определении страховых тарифов учет воздействия может быть кошмаром (в наборах данных некоторые клиенты были здесь в течение нескольких лет — мы называем это воздействие — в то время как другие были здесь в течение нескольких месяцев или недель). Почему-то простые результаты, потому что сложнее вычислять только потому, что мы должны принимать во внимание тот факт, что воздействие является неоднородной переменной.
Подверженность при формировании страхового тарифа можно рассматривать как проблему цензурированных данных (в моем наборе данных подверженность всегда меньше 1, поскольку наблюдения являются контрактами, а не держателями полисов),
- количество претензий
за период
- количество претензий
на
)
И как всегда, переменная интереса является ненаблюдаемой, потому что мы должны оценить договор страхования с периодом покрытия один (полный) год. Таким образом, мы должны смоделировать годовую частоту страховых возмещений.
В нашем наборе данных у нас есть 




что также является средневзвешенным значением в годовом исчислении отдельных лиц.
Мы рассматриваем отношение общего количества требований к общему
риску. Эта оценка появляется, например, если мы рассмотрим пуассоновский процесс, так что 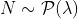

т.е.
Первое условие заказа здесь
который удовлетворен, если
Итак, у нас есть оценка ожидаемого значения, и тогда естественная оценка для 
Теперь нам нужна оценка дисперсии, или, точнее, условной переменной. Предположим (в качестве отправной точки), что все имеют одинаковую экспозицию 



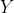




для всех значений 
Таким образом, представляется правомерным предположить , что эмпирическая дисперсия 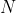
Так как среднее 

![http://latex.codecogs.com/gif.latex?S_N^2=E\cdot%20\frac{1}{n}\sum_{i=1}^n%20\left[\frac{Y_i} {Е} - \ Overline {N} \ право] ^ 2}% 20 =% 20 \ гидроразрыва {1} {N} \ sum_ {I = 1} ^ п% 20E \ влево [\ гидроразрыва {Y_i} {Е} - \ Overline {N} \ право] ^ 2}](/wp-content/uploads/images/dzo/3283f4eb6c40f6216ec64df86e220e32.latex)
![http://latex.codecogs.com/gif.latex?S_N^2=\frac{\sum_{i=1}^n%20[Y_i-\overline{N}\cdot%20E]^2%20} {} п](/wp-content/uploads/images/dzo/cac754d60f0f13d055c10be41efebe01.latex)

![http://latex.codecogs.com/gif.latex?S_N^2=\frac{\sum_{i=1}^n%20[Y_i-\overline{N}\cdot%20E_i]^2%20} {\ sum_ {I = 1} ^ п% 20E_i}](/wp-content/uploads/images/dzo/ba5c1a6172ebb5331b7d759f0354c41b.latex)

Это можно использовать для проверки правильности допущения Пуассона для частоты модели. Рассмотрим следующий набор данных,
> sinistre=read.table("http://freakonometrics.free.fr/sinistreACT2040.txt", + header=TRUE,sep=";") > sinistres=sinistre[sinistre$garantie=="1RC",] > sinistres=sinistres[sinistres$cout>0,] > contrat=read.table("http://freakonometrics.free.fr/contractACT2040.txt", + header=TRUE,sep=";") > T=table(sinistres$nocontrat) > T1=as.numeric(names(T)) > T2=as.numeric(T) > nombre1 = data.frame(nocontrat=T1,nbre=T2) > I = contrat$nocontrat%in%T1 > T1= contrat$nocontrat[I==FALSE] > nombre2 = data.frame(nocontrat=T1,nbre=0) > nombre=rbind(nombre1,nombre2) > baseFREQ = merge(contrat,nombre)
Здесь у нас есть две переменные интереса, подверженность, на контракт,
> E <- baseFREQ$exposition
и (наблюдаемое) количество требований (в течение этого периода времени)
> Y <- baseFREQ$nbre
Можно рассчитать без ковариат, среднего (годового) количества претензий по контракту и связанных с ними отклонений
> (mean=weighted.mean(Y/E,E)) [1] 0.07279295 > (variance=sum((Y-mean*E)^2)/sum(E)) [1] 0.08778567
Похоже, что дисперсия (немного) больше, чем в среднем (через несколько недель мы увидим, как ее проверить, более формально). Можно добавить ковариаты, например, плотность населения в районе проживания страхователя,
> X=as.factor(baseFREQ$densite) > for(i in 1:length(levels(X))){ + Ei=E[X==levels(X)[i]] + Yi=Y[X==levels(X)[i]] + (meani=weighted.mean(Yi/Ei,Ei)) # moyenne + (variancei=sum((Yi-meani*Ei)^2)/sum(Ei)) # variance + cat("Density, zone",levels(X)[i],"average =",meani," variance =",variancei,"\n") + } Density, zone 11 average = 0.07962411 variance = 0.08711477 Density, zone 21 average = 0.05294927 variance = 0.07378567 Density, zone 22 average = 0.09330982 variance = 0.09582698 Density, zone 23 average = 0.06918033 variance = 0.07641805 Density, zone 24 average = 0.06004009 variance = 0.06293811 Density, zone 25 average = 0.06577788 variance = 0.06726093 Density, zone 26 average = 0.0688496 variance = 0.07126078 Density, zone 31 average = 0.07725273 variance = 0.09067 Density, zone 41 average = 0.03649222 variance = 0.03914317 Density, zone 42 average = 0.08333333 variance = 0.1004027 Density, zone 43 average = 0.07304602 variance = 0.07209618 Density, zone 52 average = 0.06893741 variance = 0.07178091 Density, zone 53 average = 0.07725661 variance = 0.07811935 Density, zone 54 average = 0.07816105 variance = 0.08947993 Density, zone 72 average = 0.08579731 variance = 0.09693305 Density, zone 73 average = 0.04943033 variance = 0.04835521 Density, zone 74 average = 0.1188611 variance = 0.1221675 Density, zone 82 average = 0.09345635 variance = 0.09917425 Density, zone 83 average = 0.04299708 variance = 0.05259835 Density, zone 91 average = 0.07468126 variance = 0.3045718 Density, zone 93 average = 0.08197912 variance = 0.09350102 Density, zone 94 average = 0.03140971 variance = 0.04672329
Возможно, графики будут хорошим инструментом для визуализации этой информации.
> plot(meani,variancei,cex=sqrt(Ei),col="grey",pch=19, + xlab="Empirical average",ylab="Empirical variance") > points(meani,variancei,cex=sqrt(Ei))
Размер кружков связан с размером группы (площадь пропорциональна общей экспозиции в группе). Первая диагональ соответствует модели Пуассона, т.е. дисперсия должна быть равна средней. Также можно рассмотреть другие ковариаты, такие как тип газа
или марка автомобиля,
Также можно рассматривать возраст водителя как категорическое изменение
На самом деле, возраст интересен: в этом наборе данных мы можем наблюдать особенность, которую Жан-Филипп Буше наблюдал и в своих собственных наборах данных. Давайте посмотрим внимательнее, где разные возрасты,
On the right, we can observe young (unexperienced) drivers. That was expected. But some classes are belowthe first diagonal: the expected frequency is large, but not the variance. I.e. we know for sure that young drivers have more car accidents. It is not an heterogeneous class, on the contrary: young drivers can be seen as a relatively homogeneous class, with a high frequency of car accidents.
With the original dataset (here, I use only a subset with 50,000 clients), we do obtain the following graph:
If we do not observe underdispersion for young drivers, observe that those are incredibly homogeneous classes. With a clear impact of experience, since circles are moving downward from age 18 to 25.
Another disturbing story (this was – one more time – suggestion from Jean-Philippe) that it might be possible to consider the exposure as a standard variable, and see if the coefficient is actually equal to 1. Without any covariate,
> reg=glm(Y~log(E),family=poisson("log")) > summary(reg) Call: glm(formula = Y ~ log(E), family = poisson("log")) Deviance Residuals: Min 1Q Median 3Q Max -0.3988 -0.3388 -0.2786 -0.1981 12.9036 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.83045 0.02822 -100.31 <2e-16 *** log(E) 0.53950 0.02905 18.57 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 12931 on 49999 degrees of freedom Residual deviance: 12475 on 49998 degrees of freedom AIC: 16150 Number of Fisher Scoring iterations: 6
i.e. the parameter is clearly strictly smaller than 1. And it is neither related to significance,
> library(car) > linearHypothesis(reg,"log(E)",1) Linear hypothesis test Hypothesis: log(E) = 1 Model 1: restricted model Model 2: Y ~ log(E) Res.Df Df Chisq Pr(>Chisq) 1 49999 2 49998 1 251.19 < 2.2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
nor to the fact that I did not take into account covariates,
> reg=glm(nbre~log(exposition)+carburant+as.factor(ageconducteur)+as.factor(densite),family=poisson("log"),data=baseFREQ) > summary(reg) Call: glm(formula = nbre ~ log(exposition) + carburant + as.factor(ageconducteur) + as.factor(densite), family = poisson("log"), data = baseFREQ) Deviance Residuals: Min 1Q Median 3Q Max -0.7114 -0.3200 -0.2637 -0.1896 12.7104 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -14.07321 181.04892 -0.078 0.938042 log(exposition) 0.56781 0.03029 18.744 < 2e-16 *** carburantE -0.17979 0.04630 -3.883 0.000103 *** as.factor(ageconducteur)19 12.18354 181.04915 0.067 0.946348 as.factor(ageconducteur)20 12.48752 181.04902 0.069 0.945011
(etc). So it might be a too strong assumption to assume that the exposure is an exogenous variate here. But that’s another story !
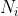 за период
за период ![http://latex.codecogs.com/gif.latex?[0,1]](/wp-content/uploads/images/dzo/ba26b5302e5434789f40bef9d3ee897d.latex)
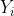 на
на ![http://latex.codecogs.com/gif.latex?[0,E_i]](/wp-content/uploads/images/dzo/51e3fb80dbb90ec735deda8bd39f3b1c.latex) )
)


![http://latex.codecogs.com/gif.latex?\mathcal {L} (\ Lambda, \ boldsymbol {Y}, \ boldsymbol {Е}) = \ prod_ {I = 1} ^ п% 20 \ гидроразрыва { е ^ {- \ Lambda% 20E_i}!% 20 [\ Lambda% 20E_i] ^ {Y_i}} {Y_i}](/wp-content/uploads/images/dzo/49df8c161856caa3a1ea535c2855a540.latex)
![http://latex.codecogs.com/gif.latex?\log%20\mathcal {L} (\ Lambda, \ boldsymbol {Y}, \ boldsymbol {Е})% 20% = 20- \ Lambda% 20 \ sum_ {I = 1} ^ п% 20E_i% 20 + \ sum_ {I = 1} ^ п% 20Y_i% 20 \ журнал [\ Lambda% 20E_i]% 20-% 20 \ журнал \ влево (\ prod_ {I = 1 } ^ п% 20Y_i! \ справа)](/wp-content/uploads/images/dzo/77f6c8e2be56651508bd5bf49ed65ba6.latex)






![http://latex.codecogs.com/gif.latex?S_N^2=\frac {1} {N} \ sum_ {I = 1} ^ п% 20 \ гидроразрыва {Е} {Е ^ 2} \ влево [ Y_i- \ Overline {N} \ CDOT% 20E \ вправо] ^ 2}% 20 = \ гидроразрыва {1} {N} \ sum_ {I = 1} ^ п% 20 \ гидроразрыва {1} {Е} [Y_i- \ Overline {N} \ CDOT% 20E] ^ 2](/wp-content/uploads/images/dzo/371191139fd08bf9a3149570f385b511.latex)
![http://latex.codecogs.com/gif.latex?S_{N|\boldsymbol{x}}^2=\frac{\sum_{i,\boldsymbol{X}_i=\boldsymbol{x}}%20 [Y_i- \ Overline {N} \ CDOT% 20E_i] ^ 2} {\ sum_ {я, \ boldsymbol {X} =-i \ boldsymbol {х}}% 20% 20E_i}](/wp-content/uploads/images/dzo/e15d47fa9bc522b3a7c48cc6bfc19e14.latex)





