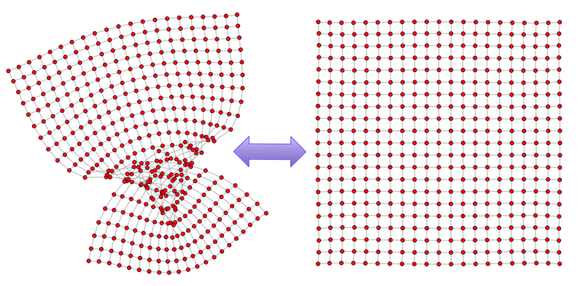
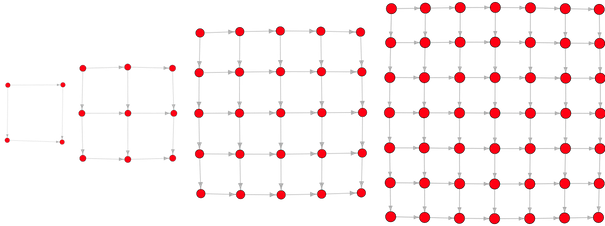
Решетка представляет собой график , который имеет определенную, четко определенную структуру. Решетка nxn — это двумерная сетка, в которой есть n ребер вдоль оси x и n ребер вдоль оси y. Пример решетки 20×20 представлен на двух изображениях выше. Обратите внимание, что оба изображения имеют «одинаковую» решетку 20×20. Независимо от того, что решетка «свернута», оба графика изоморфны друг другу (т.е. элементы находятся в взаимно однозначном соответствии друг с другом). Таким образом, в решетке важно не то, как она представлена на двумерной плоскости , а то, какова ее схема связности. Используя язык статистики R , немного базовой описательной статистики вычисляются для решетки 20×20 с именем g.
~$ r
R version 2.13.1 (2011-07-08)
Copyright (C) 2011 The R Foundation for Statistical Computing
...
> length(V(g))
[1] 441
> length(E(g))
[1] 840
> hist(degree(g), breaks=c(0,2,3,4), freq=TRUE, xlab='vertex degree', ylab='frequency', cex.lab=1.25, main='', col=c('gray10','gray40','gray70'), labels=TRUE, axes=FALSE, cex=2)
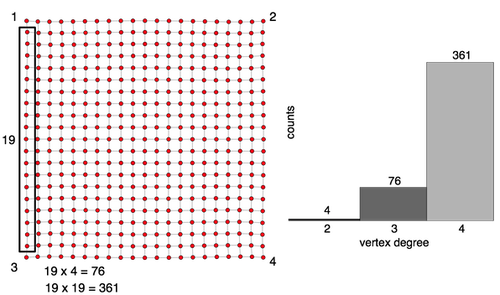
В степени статистика 20×20 решетки можно аналитически определить. Должно существовать 4 угловых вершины, каждая из которых имеет степень 2. На каждой стороне должно быть 19 вершин, каждая из которых имеет степень 3. Учитывая, что существует 4 стороны, имеется 76 вершин со степенью 3 (19 x 4 = 76). , Наконец, во внутреннем квадрате решетки существует 19 рядов из 19 вершин, каждая из которых имеет степень 4, и, следовательно, существует 361 вершина степени 4 (19 x 19 = 361). Приведенный выше фрагмент кода отображает распределение степеней решетки 20×20, что подтверждает вышеупомянутый вывод. Решетка 20×20 имеет 441 вершину и 840 ребер. В общем, число вершин в nxn решетке будет (n + 1) (n + 1), а количество ребер будет 2 ((nn) + n).
Обходы через направленную решетку
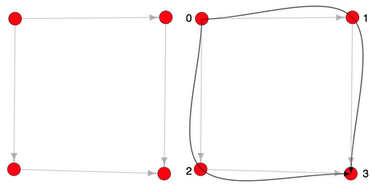
Предположим, что это направленная решетка, в которой все ребра либо указывают на вершину справа, либо ниже хвостовой вершины. В такой структуре вершина левого верхнего угла имеет только исходящие ребра. Точно так же вершина нижнего правого угла имеет только входящие ребра. Интересный вопрос, который можно задать о решетке этой формы:
«Сколько существует уникальных путей, которые начинаются от верхней левой вершины и заканчиваются в нижней правой вершине?»

0 -> 1 -> 3
0 -> 2 -> 3
Как показано выше, эти пути можно перечислить вручную , просто рисуя пути сверху-слева-внизу-справа без повторения одного и того же пути дважды. Когда решетка становится слишком большой, чтобы эффективно рисовать и рисовать вручную, можно использовать численный вычислительный метод для определения количества путей. Можно построить решетку, используя TinkerGraph Blueprints, и обойти ее, используя Gremlin . Чтобы сделать это для решетки любого размера (любого n), определена функция с именем generateLattice (int n).
def generateLattice(n) {
g = new TinkerGraph()
// total number of vertices
max = Math.pow((n+1),2)
// generate the vertices
(1..max).each { g.addVertex() }
// generate the edges
g.V.each {
id = Integer.parseInt(it.id)
right = id + 1
if (((right % (n + 1)) > 0) && (right <= max)) {
g.addEdge(it, g.v(right), '')
}
down = id + n + 1
if (down < max) {
g.addEdge(it, g.v(down), '')
}
}
return g
}
Интересное свойство путей «сверху вниз» заключается в том, что они всегда имеют одинаковую длину. Для предварительно построенной диаграммы решетки 1×1 эта длина равна 2. Следовательно, нижняя правая вершина может быть достигнута после двух шагов. В общем, количество шагов, необходимых для nxn-решетки, равно 2n.
gremlin> g = generateLattice(1)
==>tinkergraph[vertices:4 edges:4]
gremlin> g.v(0).out.out.path
==>[v[0], v[2], v[3]]
==>[v[0], v[1], v[3]]
gremlin> g.v(0).out.loop(1){it.loops <= 2}.path
==>[v[0], v[2], v[3]]
==>[v[0], v[1], v[3]]
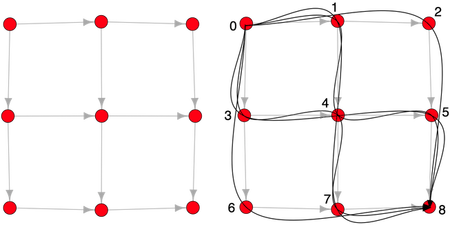
Решетка 2×2 достаточно мала, и ее пути также могут быть перечислены. Это перечисление приведено выше. Есть 6 уникальных путей. Это можно проверить в Гремлин.
gremlin> g = generateLattice(2)
==>tinkergraph[vertices:9 edges:12]
gremlin> g.v(0).out.loop(1){it.loops <= 4}.count()
==>6
gremlin> g.v(0).out.loop(1){it.loops <= 4}.path
==>[v[0], v[3], v[6], v[7], v[8]]
==>[v[0], v[3], v[4], v[7], v[8]]
==>[v[0], v[3], v[4], v[5], v[8]]
==>[v[0], v[1], v[4], v[7], v[8]]
==>[v[0], v[1], v[4], v[5], v[8]]
==>[v[0], v[1], v[2], v[5], v[8]]
Если решетка 1×1 имеет 2 пути, 2×2 6 путей, сколько путей имеет решетка 3×3? В общем, сколько путей имеет решетка nxn? В вычислительном отношении с Gremlin эти пути можно обойти и посчитать. Тем не менее, существуют ограничения для этого метода. Например, попробуйте использовать стиль обхода Gremlin, чтобы определить все уникальные пути в решетке 1000×1000. Как скоро станет ясно, Гремлин понадобится возраст вселенной , чтобы найти решение. Приведенный ниже код демонстрирует подсчет путей Гремлин до решеток размером 10х10.
gremlin> (1..10).collect{ n ->
gremlin> g = generateLattice(n)
gremlin> g.v(0).out.loop(1){it.loops <= (2*n)}.count()
gremlin> }
==>2
==>6
==>20
==>70
==>252
==>924
==>3432
==>12870
==>48620
==>184756
Решение в закрытой форме и сила аналитических методов
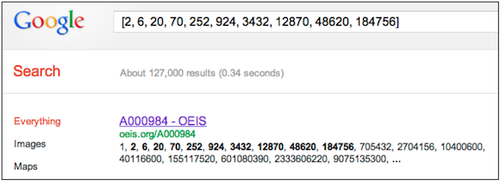
Чтобы узнать число путей через любую произвольную решетку nxn, необходимо вывести уравнение замкнутой формы . Один из способов определить уравнение замкнутой формы — просто найти последовательность в Google . Первый возвращенный сайт — онлайн-энциклопедия целочисленных последовательностей . Последовательность, обнаруженная Гремлином, называется A000984, и на странице есть следующее примечание:
«Число путей решетки от (0,0) до (n, n) с использованием шагов (1,0) и (0,1). [Йорг Арндт, 01 июля 2011]
На этой же странице указано, что общая форма «2n выберите n». Это может быть расширено до факторного представления (например, 5! = 5 * 4 * 3 * 2 * 1), как показано ниже.
Учитывая это решение в закрытой форме, явную структуру графа не нужно пересматривать. Вместо этого комбинаторное уравнение может быть оценено для любого n. Направленная решетка 20×20 имеет более 137 миллиардов уникальных путей ! Это количество путей слишком велико, чтобы Гремлин мог перечислить их за разумное время.
> n = 20 > factorial(2 * n) / factorial(n)^2 [1] 137846528820
Вопрос, который можно задать: «Как 2n выбирает 2, объясняет количество путей через решетку nxn?» При подсчете количества путей от вершины (0,0) до (n, n), где разрешены только движения вниз и вправо, должно быть n движений вниз и n движений вправо. Это означает, что всего 2n ходов, и, как таковые, есть n вариантов (так как другие n «вариантов выбора» вызываются предыдущими n вариантами). Таким образом, общее количество ходов равно «2n выбрать n». Эта та же самая целочисленная последовательность также найдена в другой, казалось бы, не связанной проблеме (предоставленной той же веб-страницей).
«Число возможных значений двоичного числа размером 2 * n, для которого половина битов включена, а половина выключена. — Гэвин Скотт, 9 августа 2003 года
Each move is a sequence of letters that contains n Ds and n Rs, where down twice then right twice would be DDRR. This maps the “lattice problem” onto the “binary string of length 2n problem.” Both problems are essentially realizing the same behavior via two different representations.
Plotting the Growth of a Function
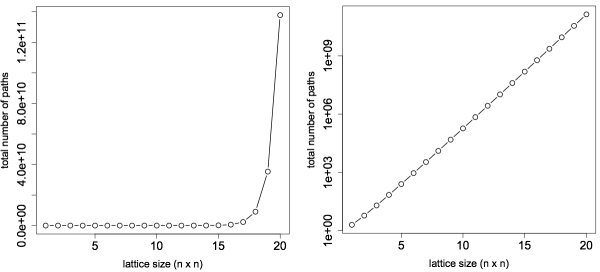
It is possible to plot the combinatorial function over the sequence 1 to 20 (left plot below). What is interesting to note is that when the y-axis of the plot is set to a log-scale, the plot is a straight line (right plot below). This means that the number of paths in a directed lattice grows exponentially as the size of the lattice grows linear.
> factorial(2 * seq(1,n)) / factorial(seq(1,n))^2 [1] 2 6 20 70 252 924 [7] 3432 12870 48620 184756 705432 2704156 [13] 10400600 40116600 155117520 601080390 2333606220 9075135300 [19] 35345263800 137846528820 > x <- factorial(2 * seq(1,n)) / factorial(seq(1,n))^2 > plot(x, xlab='lattice size (n x n)', ylab='total number of paths', cex.lab=1.4, cex.axis=1.6, lwd=1.5, cex=1.5, type='b') > plot(x, xlab='lattice size (n x n)', ylab="total number of paths", cex.lab=1.4, cex.axis=1.6, lwd=1.5, cex=1.5, type='b' log='y')
Conclusion
It is wild to think that a 20×20 lattice, with only 441 vertices and 840 edges, has over 137 billion unique directed paths from top-left to bottom-right. It’s this statistic that makes it such a loopy lattice! Anyone using graphs should take heed. The graph data structure is not like its simpler counterparts (e.g. the list, map, and tree). The connectivity patterns of a graph can yield combinatorial explosions. When working with graphs, it’s important to understand this behavior. It’s very easy to run into situations, where if all the time in the universe doesn’t exist, then neither does a solution.
Acknowledgments
This exploration was embarked on with Dr. Vadas Gintautas. Vadas has published high-impact journal articles on a variety of problems involving biological networks, information theory, computer vision, and nonlinear dynamics. He holds a Ph.D. in Physics from the University of Illinois at Urbana Champaign.
Finally, this post was inspired by Project Euler. Project Euler is a collection of math and programming challenges. Problem 15 asks, “How many routes are there through a 20×20 grid?”