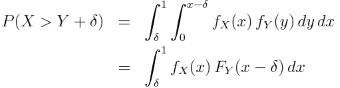Кто-то вчера попросил меня код R для вычисления вероятности P ( X > Y + δ), где X и Y — независимые бета-случайные величины. Я выкладываю решение здесь на случай, если оно принесет пользу кому-то еще
Пример того, почему вы можете захотеть вычислить эту вероятность, см. В байесовском представлении реселлеров Amazon .
Пусть X — бета (a, b) случайная величина, а Y — бета (c, d) случайная величина. Обозначим PDF-файлы f, а CDF- F . Тогда вероятность, что нам нужно
Если вам просто нужно вычислить эту вероятность несколько раз, вот настольное приложение для вычисления случайных неравенств.
Но если вам нужно повторить это вычисление внутри кода R, вы можете использовать следующее.
beta.ineq <- function(a, b, c, d, delta)
{
integrand <- function(x) { dbeta(x, a, b)*pbeta(x-delta, c, d) }
integrate(integrand, delta, 1, rel.tol=1e-4)$value
}
Код такой же хороший или плохой, как и integrateфункция R. Вероятно, это достаточно точно, если ни один из параметров a , b , c или d не близок к нулю. Когда один или несколько из этих параметров малы, сложнее вычислить интеграл.
В приведенном выше коде нет проверки ошибок. Более надежная версия будет проверять, что все параметры положительны и что deltaменьше 1.
Вот решение соответствующей проблемы для гамма-случайных величин, при условии, что deltaоно равно нулю: поддержка в одну строку .
А вот и серия постов в блоге о случайном неравенстве.
Введение
Аналитические результаты
Численные результаты
Распределения Коши
Бета-распределения
Гамма-распределения
Три или более случайных величин
Сложенные нормали