AI с Python — обучение без учителя: кластеризация

Необслуживаемые алгоритмы машинного обучения не имеют какого-либо руководителя, обеспечивающего какое-либо руководство. Вот почему они тесно связаны с тем, что некоторые называют истинным искусственным интеллектом.

При неконтролируемом обучении не будет правильного ответа и учителя для руководства. Алгоритмы должны обнаружить интересную закономерность в данных для обучения.

Что такое кластеризация?

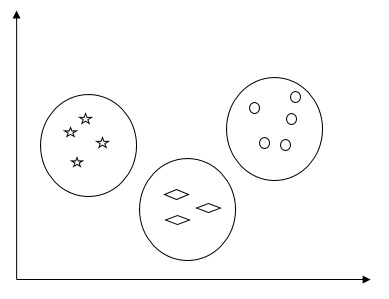
По сути, это тип неконтролируемого метода обучения и распространенный метод статистического анализа данных, используемый во многих областях. Кластеризация главным образом является задачей разделения набора наблюдений на подмножества, называемые кластерами, таким образом, чтобы наблюдения в одном и том же кластере были похожи в одном смысле и не похожи на наблюдения в других кластерах. Проще говоря, мы можем сказать, что главная цель кластеризации — группировать данные на основе сходства и различий.

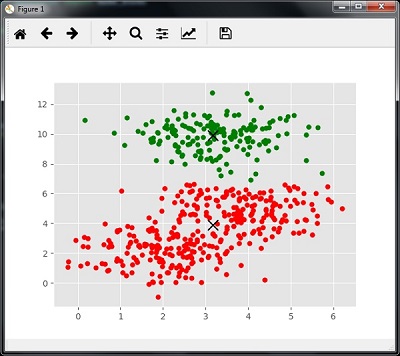
Например, следующая диаграмма показывает аналогичные данные в разных кластерах —

Алгоритмы кластеризации данных

Ниже приведены несколько распространенных алгоритмов кластеризации данных.

Алгоритм K-средних

Алгоритм кластеризации K-средних является одним из известных алгоритмов кластеризации данных. Нужно предположить, что номера кластеров уже известны. Это также называется плоской кластеризацией. Это алгоритм итеративной кластеризации. Для этого алгоритма необходимо выполнить следующие шаги:

Шаг 1 — Нам нужно указать желаемое количество K подгрупп.

Шаг 2 — Зафиксируйте количество кластеров и случайным образом назначьте каждую точку данных кластеру. Или, другими словами, нам нужно классифицировать наши данные на основе количества кластеров.

На этом этапе кластерные центроиды должны быть вычислены.

Поскольку это итеративный алгоритм, нам нужно обновлять местоположения K центроидов с каждой итерацией, пока мы не найдем глобальные оптимумы или, другими словами, центроиды достигают в своих оптимальных местоположениях.

Следующий код поможет в реализации алгоритма кластеризации K-средних в Python. Мы собираемся использовать модуль Scikit-learn.

Давайте импортируем необходимые пакеты —

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

Следующая строка кода поможет в создании двумерного набора данных, содержащего четыре больших объекта , с помощью make_blob из пакета sklearn.dataset .

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples = 500, centers = 4,
            cluster_std = 0.40, random_state = 0)

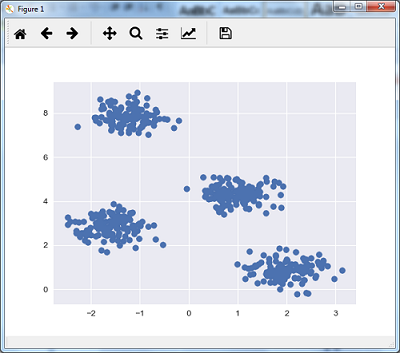
Мы можем визуализировать набор данных, используя следующий код —

plt.scatter(X[:, 0], X[:, 1], s = 50);
plt.show()

Здесь мы инициализируем kmeans в качестве алгоритма KMeans с обязательным параметром количества кластеров (n_clusters).

kmeans = KMeans(n_clusters = 4)

Нам нужно обучить модель K-средних с входными данными.

kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c = y_kmeans, s = 50, cmap = 'viridis')

centers = kmeans.cluster_centers_

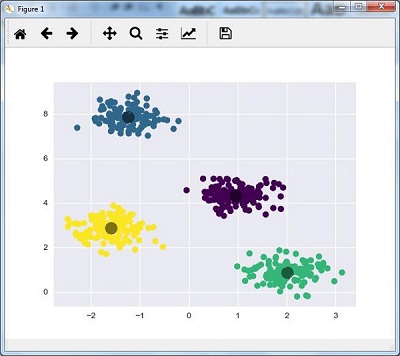
Код, приведенный ниже, поможет нам построить и визуализировать результаты работы машины на основе наших данных, а также в соответствии с количеством найденных кластеров.

plt.scatter(centers[:, 0], centers[:, 1], c = 'black', s = 200, alpha = 0.5);
plt.show()

Алгоритм среднего смещения

Это еще один популярный и мощный алгоритм кластеризации, используемый в обучении без учителя. Он не делает никаких предположений, следовательно, это непараметрический алгоритм. Это также называется иерархической кластеризацией или кластерным анализом среднего сдвига. Ниже приведены основные шаги этого алгоритма —

• Прежде всего, нам нужно начать с точек данных, назначенных на собственный кластер.

• Теперь он вычисляет центроиды и обновляет местоположение новых центроидов.

• Повторяя этот процесс, мы приближаемся к вершине кластера, т.е. к области более высокой плотности.

• Этот алгоритм останавливается на стадии, когда центроиды больше не двигаются.

Прежде всего, нам нужно начать с точек данных, назначенных на собственный кластер.

Теперь он вычисляет центроиды и обновляет местоположение новых центроидов.

Повторяя этот процесс, мы приближаемся к вершине кластера, т.е. к области более высокой плотности.

Этот алгоритм останавливается на стадии, когда центроиды больше не двигаются.

С помощью следующего кода мы реализуем алгоритм кластеризации Mean Shift в Python. Мы собираемся использовать модуль Scikit-learn.

Давайте импортируем необходимые пакеты —

import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")

Следующий код поможет в создании двумерного набора данных, содержащего четыре больших объекта , с помощью make_blob из пакета sklearn.dataset .

from sklearn.datasets.samples_generator import make_blobs

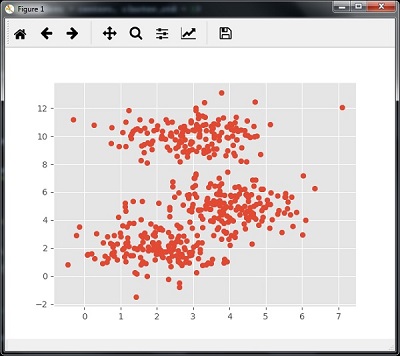
Мы можем визуализировать набор данных с помощью следующего кода

centers = [[2,2],[4,5],[3,10]]
X, _ = make_blobs(n_samples = 500, centers = centers, cluster_std = 1)
plt.scatter(X[:,0],X[:,1])
plt.show()

Теперь нам нужно обучить кластерную модель Mean Shift с использованием входных данных.

ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

Следующий код напечатает центры кластеров и ожидаемое количество кластеров согласно входным данным —

print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
[[ 3.23005036 3.84771893]
[ 3.02057451 9.88928991]]
Estimated clusters: 2

Код, приведенный ниже, поможет построить и визуализировать результаты работы машины на основе наших данных, а также соответствия в соответствии с количеством найденных кластеров.

colors = 10*['r.','g.','b.','c.','k.','y.','m.']
   for i in range(len(X)):
   plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 10)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
   marker = "x",color = 'k', s = 150, linewidths = 5, zorder = 10)
plt.show()

Измерение производительности кластеризации

Данные реального мира не организованы естественным образом в несколько отличительных кластеров. По этой причине нелегко визуализировать и делать выводы. Вот почему нам необходимо измерять производительность кластеризации, а также ее качество. Это можно сделать с помощью анализа силуэта.

Анализ силуэта

Этот метод может использоваться для проверки качества кластеризации путем измерения расстояния между кластерами. По сути, это дает возможность оценить такие параметры, как количество кластеров, путем оценки силуэта. Эта оценка является метрикой, которая измеряет, насколько близко каждая точка в одном кластере находится к точкам в соседних кластерах.

Анализ силуэта баллов

Счет имеет диапазон [-1, 1]. Ниже приводится анализ этой оценки —

• Оценка +1 — Оценка около +1 означает, что выборка находится далеко от соседнего кластера.

• Оценка 0 — Оценка 0 указывает на то, что выборка находится или очень близка к границе решения между двумя соседними кластерами.

• Оценка -1 — Отрицательная оценка означает, что выборки были назначены в неправильные кластеры.

Оценка +1 — Оценка около +1 означает, что выборка находится далеко от соседнего кластера.

Оценка 0 — Оценка 0 указывает на то, что выборка находится или очень близка к границе решения между двумя соседними кластерами.

Оценка -1 — Отрицательная оценка означает, что выборки были назначены в неправильные кластеры.

Расчет силуэта

В этом разделе мы узнаем, как рассчитать оценку силуэта.

Оценка силуэта может быть рассчитана по следующей формуле:

$$силуэт счет = \ frac {\ left (pq \ right)} {max \ left (p, q \ right)}$$

Здесь ? — среднее расстояние до точек в ближайшем кластере, частью которых точка данных не является. И, ? — среднее расстояние внутри кластера до всех точек его собственного кластера.

Чтобы найти оптимальное количество кластеров, нам нужно снова запустить алгоритм кластеризации, импортировав модуль метрик из пакета sklearn . В следующем примере мы запустим алгоритм кластеризации K-средних, чтобы найти оптимальное количество кластеров:

Импортируйте необходимые пакеты, как показано на рисунке —

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

С помощью следующего кода мы сгенерируем двумерный набор данных, содержащий четыре больших объекта, используя make_blob из пакета sklearn.dataset .

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples = 500, centers = 4, cluster_std = 0.40, random_state = 0)

Инициализируйте переменные как показано —

scores = []
values = np.arange(2, 10)

Нам нужно пройти через модель K-средних по всем значениям, а также обучить ее входным данным.

for num_clusters in values:
kmeans = KMeans(init = 'k-means++', n_clusters = num_clusters, n_init = 10)
kmeans.fit(X)

Теперь оцените оценку силуэта для текущей модели кластеризации, используя евклидову метрику расстояния —

score = metrics.silhouette_score(X, kmeans.labels_,
metric = 'euclidean', sample_size = len(X))

Следующая строка кода поможет в отображении количества кластеров, а также показателя Силуэт.

print("\nNumber of clusters =", num_clusters)
print("Silhouette score =", score)
scores.append(score)

Вы получите следующий вывод —

Number of clusters = 9
Silhouette score = 0.340391138371

num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)

Теперь вывод для оптимального количества кластеров будет следующим:

Optimal number of clusters = 2

Нахождение ближайших соседей

Если мы хотим создать рекомендательные системы, такие как система рекомендования фильмов, то нам нужно понять концепцию поиска ближайших соседей. Это потому, что система рекомендации использует концепцию ближайших соседей.

Концепция нахождения ближайших соседей может быть определена как процесс нахождения ближайшей точки к точке входа из данного набора данных. Основное использование этого алгоритма KNN) K-ближайших соседей) заключается в создании систем классификации, которые классифицируют точку данных о близости точки входных данных к различным классам.

Код Python, приведенный ниже, помогает найти K-ближайших соседей заданного набора данных —

Импортируйте необходимые пакеты, как показано ниже. Здесь мы используем модуль NearestNeighbors из пакета sklearn

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors

Давайте теперь определим входные данные —

A = np.array([[3.1, 2.3], [2.3, 4.2], [3.9, 3.5], [3.7, 6.4], [4.8, 1.9], 
             [8.3, 3.1], [5.2, 7.5], [4.8, 4.7], [3.5, 5.1], [4.4, 2.9],])

Теперь нам нужно определить ближайших соседей —

k = 3

Нам также нужно предоставить тестовые данные, из которых можно найти ближайших соседей —

test_data = [3.3, 2.9]

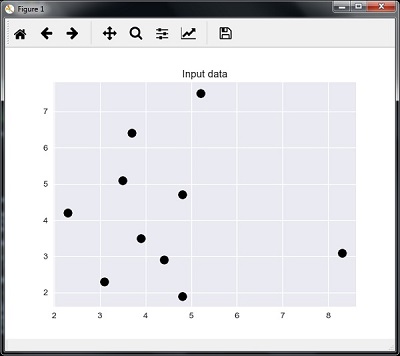
Следующий код может визуализировать и построить входные данные, определенные нами —

plt.figure()
plt.title('Input data')
plt.scatter(A[:,0], A[:,1], marker = 'o', s = 100, color = 'black')

Теперь нам нужно построить ближайший сосед. Объект также должен быть обучен

knn_model = NearestNeighbors(n_neighbors = k, algorithm = 'auto').fit(X)
distances, indices = knn_model.kneighbors([test_data])

Теперь мы можем напечатать K ближайших соседей следующим образом

print("\nK Nearest Neighbors:")
for rank, index in enumerate(indices[0][:k], start = 1):
   print(str(rank) + " is", A[index])

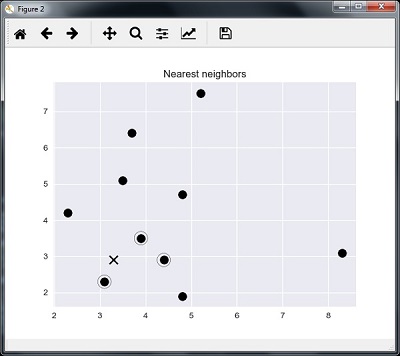
Мы можем визуализировать ближайших соседей вместе с тестовой точкой данных

plt.figure()
plt.title('Nearest neighbors')
plt.scatter(A[:, 0], X[:, 1], marker = 'o', s = 100, color = 'k')
plt.scatter(A[indices][0][:][:, 0], A[indices][0][:][:, 1],
   marker = 'o', s = 250, color = 'k', facecolors = 'none')
plt.scatter(test_data[0], test_data[1],
   marker = 'x', s = 100, color = 'k')
plt.show()

Выход

K Ближайшие соседи

1 is [ 3.1 2.3]
2 is [ 3.9 3.5]
3 is [ 4.4 2.9]

Классификатор ближайших соседей

Классификатор K-ближайших соседей (KNN) — это классификационная модель, которая использует алгоритм ближайших соседей для классификации данной точки данных. Мы реализовали алгоритм KNN в последнем разделе, а теперь мы собираемся построить классификатор KNN, используя этот алгоритм.

Концепция классификатора КНН

Основная концепция классификации K-ближайших соседей состоит в том, чтобы найти заранее определенное число, т. Е. «K» — обучающих выборок, ближайших по расстоянию к новой выборке, которую необходимо классифицировать. Новые образцы получат свою этикетку от самих соседей. Классификаторы KNN имеют фиксированную пользовательскую константу для числа соседей, которые должны быть определены. Для расстояния стандартное евклидово расстояние является наиболее распространенным выбором. Классификатор KNN работает непосредственно с изученными образцами, а не создает правила обучения. Алгоритм KNN является одним из самых простых алгоритмов машинного обучения. Это было довольно успешно в большом количестве проблем классификации и регрессии, например, распознавания символов или анализа изображений.

пример

Мы строим классификатор KNN для распознавания цифр. Для этого мы будем использовать набор данных MNIST. Мы напишем этот код в блокноте Jupyter.

Импортируйте необходимые пакеты, как показано ниже.

Здесь мы используем модуль KNeighborsClassifier из пакета sklearn.neighbors —

from sklearn.datasets import *
import pandas as pd
%matplotlib inline
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as np

Следующий код будет отображать изображение цифры, чтобы проверить, какое изображение мы должны проверить —

def Image_display(i):
   plt.imshow(digit['images'][i],cmap = 'Greys_r')
   plt.show()

Теперь нам нужно загрузить набор данных MNIST. На самом деле всего 1797 изображений, но мы используем первые 1600 изображений в качестве обучающего образца, а оставшиеся 197 будут сохранены для целей тестирования.

digit = load_digits()
digit_d = pd.DataFrame(digit['data'][0:1600])

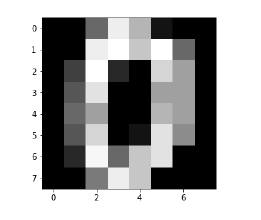
Теперь при отображении изображений мы можем видеть вывод следующим образом:

Image_display(0)

Image_display (0)

Изображение 0 отображается следующим образом —

Image_display (9)

Изображение 9 отображается следующим образом —

digit.keys ()

Теперь нам нужно создать набор данных обучения и тестирования и предоставить набор данных тестирования для классификаторов KNN.

train_x = digit['data'][:1600]
train_y = digit['target'][:1600]
KNN = KNeighborsClassifier(20)
KNN.fit(train_x,train_y)

Следующий вывод создаст конструктор классификатора ближайшего соседа —

KNeighborsClassifier(algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
   metric_params = None, n_jobs = 1, n_neighbors = 20, p = 2,
   weights = 'uniform')

Нам нужно создать тестовый образец, указав любое произвольное число больше 1600, которое было обучающим образцом.

test = np.array(digit['data'][1725])
test1 = test.reshape(1,-1)
Image_display(1725)

Image_display (6)

Изображение 6 отображается следующим образом —

Теперь мы будем прогнозировать данные теста следующим образом —

KNN.predict(test1)

Приведенный выше код сгенерирует следующий вывод:

array([6])

Теперь рассмотрим следующее —

digit['target_names']

Приведенный выше код сгенерирует следующий вывод: