Нейронные сети — это параллельные вычислительные устройства, которые являются попыткой сделать компьютерную модель мозга. Основная цель заключается в разработке системы для выполнения различных вычислительных задач быстрее, чем традиционные системы. Эти задачи включают в себя распознавание и классификацию, аппроксимацию, оптимизацию и кластеризацию данных.
Что такое искусственные нейронные сети (ANN)
Искусственная нейронная сеть (ANN) — это эффективная вычислительная система, центральная тема которой заимствована из аналогии с биологическими нейронными сетями. ANN также называют искусственными нейронными системами, системами параллельной распределенной обработки и системами Connectionist. ANN получает большую коллекцию блоков, которые связаны по некоторой схеме, чтобы обеспечить связь между ними. Эти единицы, также называемые узлами или нейронами , являются простыми процессорами, которые работают параллельно.
Каждый нейрон связан с другим нейроном через канал связи . Каждая ссылка на соединение связана с весом, имеющим информацию о входном сигнале. Это наиболее полезная информация для нейронов для решения конкретной проблемы, потому что вес обычно возбуждает или подавляет передаваемый сигнал. Каждый нейрон имеет свое внутреннее состояние, которое называется сигналом активации . Выходные сигналы, которые вырабатываются после объединения входных сигналов и правила активации, могут отправляться на другие устройства.
Если вы хотите подробно изучить нейронные сети, вы можете перейти по ссылке — Искусственная нейронная сеть .
Установка полезных пакетов
Для создания нейронных сетей в Python мы можем использовать мощный пакет для нейронных сетей, который называется NeuroLab . Это библиотека базовых алгоритмов нейронных сетей с гибкими сетевыми конфигурациями и алгоритмами обучения для Python. Вы можете установить этот пакет с помощью следующей команды в командной строке —
pip install NeuroLab
Если вы используете среду Anaconda, используйте следующую команду для установки NeuroLab:
conda install -c labfabulous neurolab
Построение нейронных сетей
В этом разделе давайте построим некоторые нейронные сети на Python с помощью пакета NeuroLab.
Классификатор на основе перцептрона
Перцептроны являются строительными блоками ANN. Если вы хотите узнать больше о Перцептроне, вы можете перейти по ссылке — искусственная_неуральная_сеть
Ниже приведено пошаговое выполнение кода Python для построения простого классификатора на основе персептрона нейронной сети —
Импортируйте необходимые пакеты, как показано на рисунке —
import matplotlib.pyplot as plt import neurolab as nl
Введите значения ввода. Обратите внимание, что это пример контролируемого обучения, поэтому вам также нужно будет указать целевые значения.
input = [[0, 0], [0, 1], [1, 0], [1, 1]] target = [[0], [0], [0], [1]]
Создать сеть с 2 входами и 1 нейроном —
net = nl.net.newp([[0, 1],[0, 1]], 1)
Теперь тренируйте сеть. Здесь мы используем правило Delta для обучения.
error_progress = net.train(input, target, epochs=100, show=10, lr=0.1)
Теперь визуализируйте вывод и построите график —
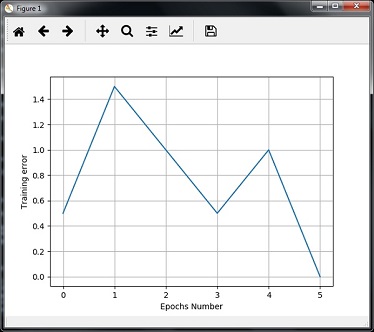
plt.figure() plt.plot(error_progress) plt.xlabel('Number of epochs') plt.ylabel('Training error') plt.grid() plt.show()
Вы можете увидеть следующий график, показывающий прогресс обучения с использованием метрики ошибки —
Однослойные нейронные сети
В этом примере мы создаем однослойную нейронную сеть, которая состоит из независимых нейронов, действующих на входные данные для получения выходных данных. Обратите внимание, что мы используем текстовый файл с именем neural_simple.txt в качестве входных данных.
Импортируйте полезные пакеты, как показано на рисунке —
import numpy as np import matplotlib.pyplot as plt import neurolab as nl
Загрузите набор данных следующим образом —
input_data = np.loadtxt(“/Users/admin/neural_simple.txt')
Ниже приведены данные, которые мы собираемся использовать. Обратите внимание, что в этих данных первые два столбца являются объектами, а последние два столбца являются метками.
array([[2. , 4. , 0. , 0. ], [1.5, 3.9, 0. , 0. ], [2.2, 4.1, 0. , 0. ], [1.9, 4.7, 0. , 0. ], [5.4, 2.2, 0. , 1. ], [4.3, 7.1, 0. , 1. ], [5.8, 4.9, 0. , 1. ], [6.5, 3.2, 0. , 1. ], [3. , 2. , 1. , 0. ], [2.5, 0.5, 1. , 0. ], [3.5, 2.1, 1. , 0. ], [2.9, 0.3, 1. , 0. ], [6.5, 8.3, 1. , 1. ], [3.2, 6.2, 1. , 1. ], [4.9, 7.8, 1. , 1. ], [2.1, 4.8, 1. , 1. ]])
Теперь разделите эти четыре столбца на 2 столбца данных и 2 метки —
data = input_data[:, 0:2] labels = input_data[:, 2:]
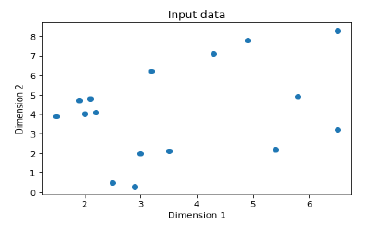
График ввода данных с помощью следующих команд —
plt.figure()
plt.scatter(data[:,0], data[:,1])
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Input data')
Теперь определите минимальное и максимальное значения для каждого измерения, как показано здесь —
dim1_min, dim1_max = data[:,0].min(), data[:,0].max() dim2_min, dim2_max = data[:,1].min(), data[:,1].max()
Затем определите количество нейронов в выходном слое следующим образом:
nn_output_layer = labels.shape[1]
Теперь определите однослойную нейронную сеть —
dim1 = [dim1_min, dim1_max] dim2 = [dim2_min, dim2_max] neural_net = nl.net.newp([dim1, dim2], nn_output_layer)
Тренируйте нейронную сеть с количеством эпох и скоростью обучения, как показано на рисунке —
error = neural_net.train(data, labels, epochs = 200, show = 20, lr = 0.01)
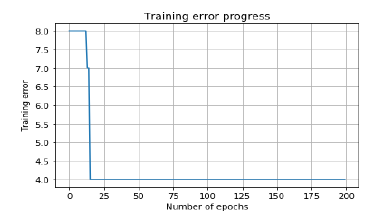
Теперь визуализируйте и нанесите на график прогресс тренировки, используя следующие команды —
plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.title('Training error progress')
plt.grid()
plt.show()
Теперь используйте тестовые данные в приведенном выше классификаторе —
print('\nTest Results:') data_test = [[1.5, 3.2], [3.6, 1.7], [3.6, 5.7],[1.6, 3.9]] for item in data_test: print(item, '-->', neural_net.sim([item])[0])
Вы можете найти результаты теста, как показано здесь —
[1.5, 3.2] --> [1. 0.] [3.6, 1.7] --> [1. 0.] [3.6, 5.7] --> [1. 1.] [1.6, 3.9] --> [1. 0.]
Вы можете увидеть следующие графики как вывод кода, обсуждавшегося до сих пор:
Многоуровневые нейронные сети
В этом примере мы создаем многослойную нейронную сеть, состоящую из более чем одного слоя, для извлечения базовых шаблонов из обучающих данных. Эта многослойная нейронная сеть будет работать как регрессор. Мы собираемся сгенерировать несколько точек данных на основе уравнения: y = 2x 2 +8.
Импортируйте необходимые пакеты, как показано на рисунке —
import numpy as np import matplotlib.pyplot as plt import neurolab as nl
Создайте некоторую точку данных на основе вышеупомянутого уравнения —
min_val = -30 max_val = 30 num_points = 160 x = np.linspace(min_val, max_val, num_points) y = 2 * np.square(x) + 8 y /= np.linalg.norm(y)
Теперь измените этот набор данных следующим образом:
data = x.reshape(num_points, 1) labels = y.reshape(num_points, 1)
Визуализируйте и нанесите на карту набор входных данных, используя следующие команды —
plt.figure()
plt.scatter(data, labels)
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Data-points')
Теперь создайте нейронную сеть, имеющую два скрытых слоя с нейролабом с десятью нейронами в первом скрытом слое, шесть во втором скрытом слое и один в выходном слое.
neural_net = nl.net.newff([[min_val, max_val]], [10, 6, 1])
Теперь используйте алгоритм обучения градиенту —
neural_net.trainf = nl.train.train_gd
Теперь обучите сеть с целью изучения данных, сгенерированных выше —
error = neural_net.train(data, labels, epochs = 1000, show = 100, goal = 0.01)
Теперь запустите нейронные сети на учебных точках данных —
output = neural_net.sim(data) y_pred = output.reshape(num_points)
Теперь сюжет и задача визуализации —
plt.figure() plt.plot(error) plt.xlabel('Number of epochs') plt.ylabel('Error') plt.title('Training error progress')
Теперь мы будем изображать фактический результат в сравнении с прогнозируемым —
x_dense = np.linspace(min_val, max_val, num_points * 2)
y_dense_pred = neural_net.sim(x_dense.reshape(x_dense.size,1)).reshape(x_dense.size)
plt.figure()
plt.plot(x_dense, y_dense_pred, '-', x, y, '.', x, y_pred, 'p')
plt.title('Actual vs predicted')
plt.show()
В результате вышеприведенных команд вы можете наблюдать графики, как показано ниже —