В этой главе мы сосредоточимся на реализации контролируемого обучения — классификации.
Методика или модель классификации пытается получить некоторые выводы из наблюдаемых значений. В задаче классификации у нас есть классифицированные результаты, такие как «Черный» или «Белый» или «Обучающие» и «Необучающие». При построении модели классификации нам нужно иметь обучающий набор данных, который содержит точки данных и соответствующие метки. Например, если мы хотим проверить, является ли изображение автомобиля или нет. Для проверки мы создадим учебный набор данных, имеющий два класса, связанных с «машиной» и «без машины». Затем нам нужно обучить модель, используя обучающие образцы. Модели классификации в основном используются для распознавания лиц, идентификации спама и т. Д.
Шаги для построения классификатора в Python
Для построения классификатора в Python мы будем использовать Python 3 и Scikit-learn, который является инструментом для машинного обучения. Выполните следующие шаги, чтобы построить классификатор в Python —
Шаг 1 — Импорт Scikit-Learn
Это был бы самый первый шаг для создания классификатора в Python. На этом этапе мы установим пакет Python под названием Scikit-learn, который является одним из лучших модулей машинного обучения в Python. Следующая команда поможет нам импортировать пакет —
Import Sklearn
Шаг 2 — Импорт набора данных Scikit-learn
На этом этапе мы можем начать работать с набором данных для нашей модели машинного обучения. Здесь мы собираемся использовать диагностическую базу данных рака молочной железы в Висконсине. Набор данных включает в себя различную информацию о раковых опухолях молочной железы, а также метки классификации злокачественных или доброкачественных . Набор данных содержит 569 экземпляров или данных о 569 опухолях и содержит информацию о 30 атрибутах или признаках, таких как радиус опухоли, текстура, гладкость и площадь. С помощью следующей команды мы можем импортировать набор данных рака молочной железы Scikit-learn —
from sklearn.datasets import load_breast_cancer
Теперь следующая команда загрузит набор данных.
data = load_breast_cancer()
Ниже приведен список важных ключей словаря —
- Имена меток классификации (target_names)
- Фактические метки (цель)
- Имена атрибутов / функций (feature_names)
- Атрибут (данные)
Теперь с помощью следующей команды мы можем создать новые переменные для каждого важного набора информации и назначить данные. Другими словами, мы можем организовать данные с помощью следующих команд —
label_names = data['target_names'] labels = data['target'] feature_names = data['feature_names'] features = data['data']
Теперь, чтобы сделать его более понятным, мы можем напечатать метки классов, метку первого экземпляра данных, имена наших функций и значение функции с помощью следующих команд:
print(label_names)
Приведенная выше команда напечатает имена классов, которые являются злокачественными и доброкачественными соответственно. Это показано как результат ниже —
['malignant' 'benign']
Теперь команда ниже покажет, что они отображаются в двоичные значения 0 и 1. Здесь 0 представляет злокачественный рак, а 1 представляет доброкачественный рак. Вы получите следующий вывод —
print(labels[0]) 0
Две команды, приведенные ниже, создадут имена и значения функций.
print(feature_names[0]) mean radius print(features[0]) [ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03 1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01 2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01 8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02 5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03 2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03 1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01 4.60100000e-01 1.18900000e-01]
Из вышеприведенного вывода видно, что первый экземпляр данных представляет собой злокачественную опухоль, радиус которой составляет 1.7990000e + 01.
Шаг 3 — Организация данных в наборы
На этом этапе мы разделим наши данные на две части, а именно обучающий набор и тестовый набор. Разделение данных на эти наборы очень важно, потому что мы должны проверить нашу модель на невидимых данных. Чтобы разделить данные на наборы, в sklearn есть функция под названием train_test_split () . С помощью следующих команд мы можем разделить данные в этих наборах:
from sklearn.model_selection import train_test_split
Приведенная выше команда импортирует функцию train_test_split из sklearn, а приведенная ниже команда разделит данные на данные обучения и тестирования. В приведенном ниже примере мы используем 40% данных для тестирования, а оставшиеся данные будут использованы для обучения модели.
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)
Шаг 4 — Построение модели
На этом этапе мы будем строить нашу модель. Мы собираемся использовать наивный байесовский алгоритм для построения модели. Следующие команды могут быть использованы для построения модели —
from sklearn.naive_bayes import GaussianNB
Приведенная выше команда импортирует модуль GaussianNB. Теперь следующая команда поможет вам инициализировать модель.
gnb = GaussianNB()
Мы будем обучать модель, подгоняя ее к данным с помощью gnb.fit ().
model = gnb.fit(train, train_labels)
Шаг 5 — Оценка модели и ее точности
На этом этапе мы собираемся оценить модель, сделав прогнозы на наших тестовых данных. Тогда мы узнаем и его точность. Для прогнозирования мы будем использовать функцию предиката (). Следующая команда поможет вам сделать это —
preds = gnb.predict(test) print(preds) [1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]
Приведенные выше серии 0 и 1 являются предсказанными значениями для классов опухолей — злокачественных и доброкачественных.
Теперь, сравнивая два массива, а именно test_labels и preds , мы можем выяснить точность нашей модели. Мы будем использовать функцию precision_score () для определения точности. Рассмотрим следующую команду для этого —
from sklearn.metrics import accuracy_score print(accuracy_score(test_labels,preds)) 0.951754385965
Результат показывает, что классификатор NaïveBayes имеет точность 95,17%.
Таким образом, с помощью описанных выше шагов мы можем построить наш классификатор в Python.
Сборка классификатора в Python
В этом разделе мы узнаем, как построить классификатор в Python.
Наивный байесовский классификатор
Наивный байесовский метод — это метод классификации, используемый для построения классификатора с использованием теоремы Байеса. Предполагается, что предикторы независимы. Проще говоря, это предполагает, что наличие определенной функции в классе не связано с наличием любой другой функции. Для построения наивного байесовского классификатора нам нужно использовать библиотеку python под названием scikit learn. Существует три типа наивных байесовских моделей, названные Gaussian, Multinomial и Bernoulli .
Для построения наивной модели байесовского классификатора машинного обучения нам нужно следующее & минус
Dataset
Мы собираемся использовать набор данных с именем База данных диагностики рака молочной железы в Висконсине. Набор данных включает в себя различную информацию о раковых опухолях молочной железы, а также метки классификации злокачественных или доброкачественных . Набор данных содержит 569 экземпляров или данных о 569 опухолях и содержит информацию о 30 атрибутах или признаках, таких как радиус опухоли, текстура, гладкость и площадь. Мы можем импортировать этот набор данных из пакета sklearn.
Наивная байесовская модель
Для построения наивного байесовского классификатора нам нужна наивная байесовская модель. Как говорилось ранее, существует три типа наивных байесовских моделей: Гауссовская, Многочленовая и Бернуллиевская . Здесь, в следующем примере мы будем использовать гауссовскую наивную байесовскую модель.
Используя вышеизложенное, мы собираемся построить наивную модель машинного обучения Байеса, чтобы использовать информацию о опухоли, чтобы предсказать, является ли опухоль злокачественной или доброкачественной.
Для начала нам нужно установить модуль sklearn. Это можно сделать с помощью следующей команды —
Import Sklearn
Теперь нам нужно импортировать набор данных с именем База данных диагностики рака молочной железы в Висконсине.
from sklearn.datasets import load_breast_cancer
Теперь следующая команда загрузит набор данных.
data = load_breast_cancer()
Данные могут быть организованы следующим образом —
label_names = data['target_names'] labels = data['target'] feature_names = data['feature_names'] features = data['data']
Теперь, чтобы прояснить ситуацию, мы можем напечатать метки классов, метку первого экземпляра данных, имена наших функций и значение функции с помощью следующих команд:
print(label_names)
Приведенная выше команда напечатает имена классов, которые являются злокачественными и доброкачественными соответственно. Это показано как результат ниже —
['malignant' 'benign']
Теперь приведенная ниже команда покажет, что они отображаются в двоичные значения 0 и 1. Здесь 0 представляет злокачественный рак, а 1 представляет доброкачественный рак. Это показано как результат ниже —
print(labels[0]) 0
Следующие две команды создадут имена и их значения.
print(feature_names[0]) mean radius print(features[0]) [ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03 1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01 2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01 8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02 5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03 2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03 1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01 4.60100000e-01 1.18900000e-01]
Из вышеприведенного вывода видно, что первый экземпляр данных представляет собой злокачественную опухоль, основной радиус которой составляет 1.7990000e + 01.
Для тестирования нашей модели на невидимых данных нам нужно разделить наши данные на данные обучения и тестирования. Это можно сделать с помощью следующего кода —
from sklearn.model_selection import train_test_split
Приведенная выше команда импортирует функцию train_test_split из sklearn, а приведенная ниже команда разделит данные на данные обучения и тестирования. В приведенном ниже примере мы используем 40% данных для тестирования, а данные напоминания будут использованы для обучения модели.
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)
Теперь мы строим модель с помощью следующих команд:
from sklearn.naive_bayes import GaussianNB
Приведенная выше команда импортирует модуль GaussianNB . Теперь с помощью команды, приведенной ниже, нам нужно инициализировать модель.
gnb = GaussianNB()
Мы будем обучать модель, подгоняя ее к данным с помощью gnb.fit () .
model = gnb.fit(train, train_labels)
Теперь оцените модель, сделав прогноз на тестовых данных, и это можно сделать следующим образом:
preds = gnb.predict(test) print(preds) [1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]
Вышеуказанные серии 0 и 1 являются предсказанными значениями для классов опухолей, т.е. злокачественных и доброкачественных.
Теперь, сравнивая два массива, а именно test_labels и preds , мы можем выяснить точность нашей модели. Мы будем использовать функцию precision_score () для определения точности. Рассмотрим следующую команду —
from sklearn.metrics import accuracy_score print(accuracy_score(test_labels,preds)) 0.951754385965
Результат показывает, что классификатор NaïveBayes имеет точность 95,17%.
Это был классификатор машинного обучения, основанный на наивной модели Байса-Гаусса.
Машины опорных векторов (SVM)
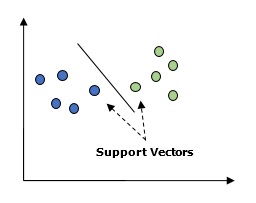
По сути, машина опорных векторов (SVM) — это контролируемый алгоритм машинного обучения, который может использоваться как для регрессии, так и для классификации. Основная концепция SVM заключается в построении каждого элемента данных в виде точки в n-мерном пространстве, причем значением каждого объекта является значение определенной координаты. Здесь n будет теми функциями, которые у нас были бы. Ниже приводится простое графическое представление, чтобы понять концепцию SVM —
На приведенной выше диаграмме у нас есть две особенности. Следовательно, сначала нам нужно построить эти две переменные в двухмерном пространстве, где каждая точка имеет две координаты, называемые опорными векторами. Линия разбивает данные на две разные классифицированные группы. Эта строка будет классификатором.
Здесь мы собираемся создать классификатор SVM, используя scikit-learn и набор данных iris. Библиотека Scikitlearn имеет модуль sklearn.svm и предоставляет sklearn.svm.svc для классификации. Классификатор SVM для прогнозирования класса растения радужки на основе 4 признаков показан ниже.
Dataset
Мы будем использовать набор данных iris, который содержит 3 класса по 50 экземпляров каждый, где каждый класс относится к типу растения радужной оболочки. Каждый экземпляр имеет четыре особенности, а именно длину чашелистика, ширину чашелистика, длину лепестка и ширину лепестка. Классификатор SVM для прогнозирования класса растения радужки на основе 4 признаков показан ниже.
ядро
Это методика, используемая SVM. В основном это функции, которые занимают низкоразмерное пространство ввода и преобразуют его в пространство более высокого измерения. Это превращает неразделимую проблему в отделимую проблему. Функция ядра может быть любой из линейной, полиномиальной, rbf и сигмоидальной. В этом примере мы будем использовать линейное ядро.
Давайте теперь импортируем следующие пакеты —
import pandas as pd import numpy as np from sklearn import svm, datasets import matplotlib.pyplot as plt
Теперь загрузите входные данные —
iris = datasets.load_iris()
Мы берем первые две функции —
X = iris.data[:, :2] y = iris.target
Мы построим границы опорных векторов с исходными данными. Мы создаем меш для построения графика.
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 h = (x_max / x_min)/100 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) X_plot = np.c_[xx.ravel(), yy.ravel()]
Нам нужно дать значение параметра регуляризации.
C = 1.0
Нам нужно создать объект классификатора SVM.
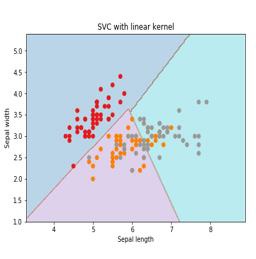
Svc_classifier = svm_classifier.SVC(kernel='linear', C=C, decision_function_shape = 'ovr').fit(X, y) Z = svc_classifier.predict(X_plot) Z = Z.reshape(xx.shape) plt.figure(figsize = (15, 5)) plt.subplot(121) plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3) plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1) plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.xlim(xx.min(), xx.max()) plt.title('SVC with linear kernel')
Логистическая регрессия
По сути, модель логистической регрессии является одним из членов семейства алгоритмов контролируемой классификации. Логистическая регрессия измеряет взаимосвязь между зависимыми переменными и независимыми переменными путем оценки вероятностей с использованием логистической функции.
Здесь, если мы говорим о зависимых и независимых переменных, то зависимая переменная — это переменная целевого класса, которую мы собираемся прогнозировать, а с другой стороны, независимые переменные — это функции, которые мы собираемся использовать для прогнозирования целевого класса.
В логистической регрессии оценка вероятностей означает прогнозирование вероятности возникновения события. Например, владелец магазина хотел бы предсказать, покупатель, вошедший в магазин, купит игровую приставку (например) или нет. Там будет много особенностей клиента — пол, возраст и т. Д., Которые будет наблюдать продавец магазина, чтобы предсказать вероятность возникновения, то есть, покупка игровой приставки или нет. Логистическая функция — это сигмовидная кривая, которая используется для построения функции с различными параметрами.
Предпосылки
Перед созданием классификатора с использованием логистической регрессии нам необходимо установить пакет Tkinter в нашей системе. Его можно установить по адресу https://docs.python.org/2/library/tkinter.html .
Теперь с помощью приведенного ниже кода мы можем создать классификатор с помощью логистической регрессии —
Сначала мы импортируем несколько пакетов —
import numpy as np from sklearn import linear_model import matplotlib.pyplot as plt
Теперь нам нужно определить пример данных, который можно сделать следующим образом:
X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4], [3.2, 0.9], [2.9, 1.9],[2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]]) y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])
Далее нам нужно создать классификатор логистической регрессии, что можно сделать следующим образом:
Classifier_LR = linear_model.LogisticRegression(solver = 'liblinear', C = 75)
Последнее, но не менее важное, мы должны обучить этот классификатор —
Classifier_LR.fit(X, y)
Теперь, как мы можем визуализировать вывод? Это можно сделать, создав функцию с именем Logistic_visualize () —
Def Logistic_visualize(Classifier_LR, X, y): min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0 min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0
В приведенной выше строке мы определили минимальное и максимальное значения X и Y, которые будут использоваться в сетке сетки. Кроме того, мы определим размер шага для построения сетки.
mesh_step_size = 0.02
Давайте определим сетку сетки значений X и Y следующим образом:
x_vals, y_vals = np.meshgrid(np.arange(min_x, max_x, mesh_step_size), np.arange(min_y, max_y, mesh_step_size))
С помощью следующего кода мы можем запустить классификатор на сетке сетки —
output = classifier.predict(np.c_[x_vals.ravel(), y_vals.ravel()]) output = output.reshape(x_vals.shape) plt.figure() plt.pcolormesh(x_vals, y_vals, output, cmap = plt.cm.gray) plt.scatter(X[:, 0], X[:, 1], c = y, s = 75, edgecolors = 'black', linewidth=1, cmap = plt.cm.Paired)
Следующая строка кода укажет границы участка
plt.xlim(x_vals.min(), x_vals.max()) plt.ylim(y_vals.min(), y_vals.max()) plt.xticks((np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0))) plt.yticks((np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0))) plt.show()
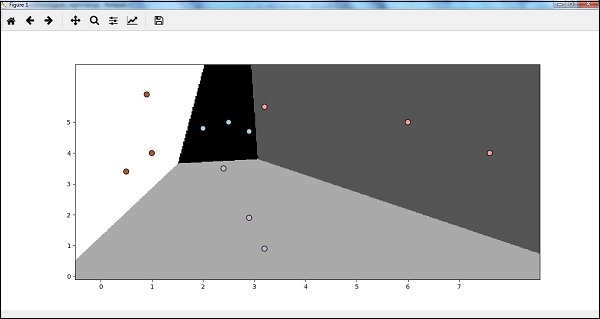
Теперь, после выполнения кода, мы получим следующий вывод, классификатор логистической регрессии —
Классификатор дерева решений
Дерево решений — это, по сути, блок-схема двоичного дерева, где каждый узел разделяет группу наблюдений в соответствии с некоторой характеристической переменной.
Здесь мы строим классификатор дерева решений для прогнозирования мужчин или женщин. Мы возьмем очень маленький набор данных, имеющий 19 образцов. Эти образцы будут состоять из двух признаков — «рост» и «длина волос».
необходимое условие
Для построения следующего классификатора нам нужно установить pydotplus и graphviz . По сути, graphviz — это инструмент для рисования графики с использованием точечных файлов, а pydotplus — это модуль для языка Graphviz’s Dot. Его можно установить с помощью менеджера пакетов или pip.
Теперь мы можем построить классификатор дерева решений с помощью следующего кода Python —
Для начала давайте импортируем некоторые важные библиотеки следующим образом:
import pydotplus from sklearn import tree from sklearn.datasets import load_iris from sklearn.metrics import classification_report from sklearn import cross_validation import collections
Теперь нам нужно предоставить набор данных следующим образом:
X = [[165,19],[175,32],[136,35],[174,65],[141,28],[176,15],[131,32], [166,6],[128,32],[179,10],[136,34],[186,2],[126,25],[176,28],[112,38], [169,9],[171,36],[116,25],[196,25]] Y = ['Man','Woman','Woman','Man','Woman','Man','Woman','Man','Woman', 'Man','Woman','Man','Woman','Woman','Woman','Man','Woman','Woman','Man'] data_feature_names = ['height','length of hair'] X_train, X_test, Y_train, Y_test = cross_validation.train_test_split (X, Y, test_size=0.40, random_state=5)
После предоставления набора данных нам нужно подобрать модель, что можно сделать следующим образом:
clf = tree.DecisionTreeClassifier() clf = clf.fit(X,Y)
Предсказание может быть сделано с помощью следующего кода Python —
prediction = clf.predict([[133,37]]) print(prediction)
Мы можем визуализировать дерево решений с помощью следующего кода Python —
dot_data = tree.export_graphviz(clf,feature_names = data_feature_names,
out_file = None,filled = True,rounded = True)
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('orange', 'yellow')
edges = collections.defaultdict(list)
for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))
for edge in edges: edges[edge].sort()
for i in range(2):dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
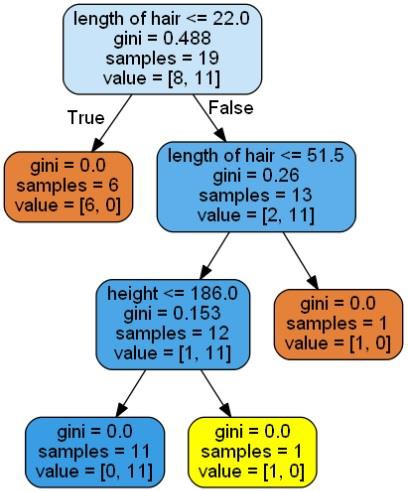
graph.write_png('Decisiontree16.png')
Это даст прогноз для приведенного выше кода как [‘Woman’] и создаст следующее дерево решений —
Мы можем изменить значения функций в прогнозе, чтобы проверить его.
Случайный лесной классификатор
Как мы знаем, методы ансамбля — это методы, которые объединяют модели машинного обучения в более мощную модель машинного обучения. Случайный лес, коллекция деревьев решений, является одним из них. Это лучше, чем одно дерево решений, потому что, сохраняя предсказательные полномочия, оно может уменьшить чрезмерную подгонку путем усреднения результатов. Здесь мы собираемся внедрить модель случайного леса в наборе данных по обучению рака.
Импортируйте необходимые пакеты —
from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import train_test_split from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() import matplotlib.pyplot as plt import numpy as np
Теперь нам нужно предоставить набор данных, который можно сделать следующим образом & минус
cancer = load_breast_cancer() X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state = 0)
После предоставления набора данных нам нужно подобрать модель, что можно сделать следующим образом:
forest = RandomForestClassifier(n_estimators = 50, random_state = 0) forest.fit(X_train,y_train)
Теперь получите точность обучения и подмножества тестирования: если мы увеличим количество оценщиков, точность подмножества тестирования также будет увеличена.
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_train,y_train))) print('Accuracy on the training subset:(:.3f)',format(forest.score(X_test,y_test)))
Выход
Accuracy on the training subset:(:.3f) 1.0 Accuracy on the training subset:(:.3f) 0.965034965034965
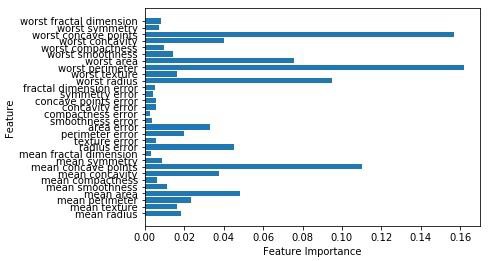
Теперь, как и дерево решений, случайный лес имеет модуль feature_importance, который обеспечит лучшее представление о весе объекта, чем дерево решений. Это можно построить и визуализировать следующим образом:
n_features = cancer.data.shape[1] plt.barh(range(n_features),forest.feature_importances_, align='center') plt.yticks(np.arange(n_features),cancer.feature_names) plt.xlabel('Feature Importance') plt.ylabel('Feature') plt.show()
Производительность классификатора
После реализации алгоритма машинного обучения нам необходимо выяснить, насколько эффективна модель. Критерии измерения эффективности могут основываться на наборах данных и метрике. Для оценки различных алгоритмов машинного обучения мы можем использовать разные показатели производительности. Например, предположим, что если для различения изображений различных объектов используется классификатор, мы можем использовать метрики эффективности классификации, такие как средняя точность, AUC и т. Д. В том или ином смысле метрика, которую мы выбираем для оценки нашей модели машинного обучения, очень важно, потому что выбор метрик влияет на то, как измеряется и сравнивается производительность алгоритма машинного обучения. Ниже приведены некоторые из показателей —
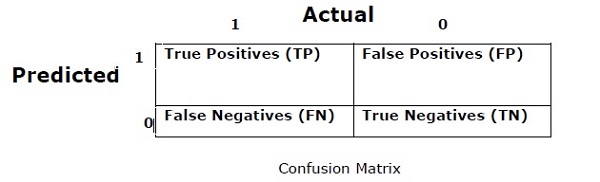
Матрица путаницы
В основном это используется для задачи классификации, где выходные данные могут быть двух или более типов классов. Это самый простой способ измерить производительность классификатора. Матрица путаницы — это, в основном, таблица с двумя измерениями, а именно: «Фактическое» и «Предсказанное». Оба измерения имеют «Истинные позитивы (TP)», «Истинные негативы (TN)», «Ложные позитивы (FP)», «Ложные негативы (FN)».
В приведенной выше матрице путаницы 1 — для положительного класса, а 0 — для отрицательного.
Ниже приведены термины, связанные с матрицей путаницы.
-
Истинные плюсы — TP — это случаи, когда фактический класс точки данных равнялся 1, а прогнозируемый — также 1.
-
True Negatives — TN — это случаи, когда фактический класс точки данных был равен 0, а прогнозируемый также равен 0.
-
Ложные положительные значения — FP — это случаи, когда фактический класс точки данных был равен 0, а прогнозируемый также равен 1.
-
False Negatives — FN — это случаи, когда фактический класс точки данных был равен 1, а прогнозируемый также равен 0.
Истинные плюсы — TP — это случаи, когда фактический класс точки данных равнялся 1, а прогнозируемый — также 1.
True Negatives — TN — это случаи, когда фактический класс точки данных был равен 0, а прогнозируемый также равен 0.
Ложные положительные значения — FP — это случаи, когда фактический класс точки данных был равен 0, а прогнозируемый также равен 1.
False Negatives — FN — это случаи, когда фактический класс точки данных был равен 1, а прогнозируемый также равен 0.
точность
Сама матрица путаницы не является показателем эффективности как таковой, но почти все матрицы производительности основаны на матрице путаницы. Одним из них является точность. В задачах классификации это может быть определено как число правильных прогнозов, сделанных моделью для всех видов сделанных прогнозов. Формула для расчета точности выглядит следующим образом:
Точность= fracTP+TNTP+FP+FN+TN
точность
В основном используется при поиске документов. Это может быть определено как сколько из возвращенных документов является правильным. Ниже приведена формула для расчета точности:
Precision= fracTPTP+FP
Напомним или Чувствительность
Это может быть определено как количество положительных результатов, возвращаемых моделью. Ниже приведена формула для расчета отзыва / чувствительности модели.
Recall= fracTPTP+FN
специфичность
Это может быть определено как количество негативов, возвращаемых моделью. Это прямо противоположно вспомнить. Ниже приведена формула для расчета специфики модели —
Specificity= fracTNTN+FP
Проблема дисбаланса класса
Классовый дисбаланс — это сценарий, в котором количество наблюдений, принадлежащих одному классу, значительно меньше, чем наблюдения, принадлежащие другим классам. Например, эта проблема видна в сценарии, где нам необходимо выявить редкие заболевания, мошеннические операции в банке и т. Д.
Пример несбалансированных классов
Давайте рассмотрим пример набора данных для обнаружения мошенничества, чтобы понять концепцию несбалансированного класса —
Total observations = 5000 Fraudulent Observations = 50 Non-Fraudulent Observations = 4950 Event Rate = 1%
Решение
Балансировка классов действует как решение несбалансированных классов. Основная цель балансирования классов — либо увеличить частоту класса меньшинства, либо уменьшить частоту класса большинства. Ниже приведены подходы к решению проблемы дисбалансов классов —
Re-Sampling
Повторная выборка представляет собой серию методов, используемых для восстановления наборов данных выборки — как обучающих наборов, так и наборов для тестирования. Повторная выборка проводится для повышения точности модели. Ниже приведены некоторые методы повторной выборки —
-
Случайное занижение выборки — этот метод направлен на то, чтобы сбалансировать распределение классов путем случайного исключения примеров большинства классов. Это делается до тех пор, пока экземпляры большинства и меньшинства не будут сбалансированы.
Случайное занижение выборки — этот метод направлен на то, чтобы сбалансировать распределение классов путем случайного исключения примеров большинства классов. Это делается до тех пор, пока экземпляры большинства и меньшинства не будут сбалансированы.
Total observations = 5000 Fraudulent Observations = 50 Non-Fraudulent Observations = 4950 Event Rate = 1%
В этом случае мы берем 10% выборок без замены из случаев не мошенничества, а затем объединяем их с примерами мошенничества —
Не мошеннические наблюдения после случайной выборки = 10% из 4950 = 495
Всего наблюдений после объединения их с мошенническими наблюдениями = 50 + 495 = 545
Следовательно, теперь частота событий для нового набора данных после выборки = 9%
Основным преимуществом этого метода является то, что он может сократить время выполнения и улучшить хранение. Но с другой стороны, он может отбрасывать полезную информацию, уменьшая при этом количество выборок обучающих данных.
-
Случайная избыточная выборка — этот метод направлен на балансирование распределения классов путем увеличения числа экземпляров в классе меньшинства путем их репликации.
Случайная избыточная выборка — этот метод направлен на балансирование распределения классов путем увеличения числа экземпляров в классе меньшинства путем их репликации.
Total observations = 5000 Fraudulent Observations = 50 Non-Fraudulent Observations = 4950 Event Rate = 1%
В случае, если мы повторяем 50 мошеннических наблюдений 30 раз, то мошеннические наблюдения после репликации наблюдений класса меньшинства будут 1500. И тогда общее количество наблюдений в новых данных после передискретизации будет 4950 + 1500 = 6450. Следовательно, частота событий для нового набора данных будет 1500/6450 = 23%.
Основным преимуществом этого метода является то, что не будет потери полезной информации. Но, с другой стороны, у него повышенные шансы переоснащения, потому что он копирует события класса меньшинства.
Техника ансамбля
Эта методология в основном используется для модификации существующих алгоритмов классификации, чтобы сделать их подходящими для несбалансированных наборов данных. При таком подходе мы строим несколько двухступенчатых классификаторов из исходных данных и затем агрегируем их прогнозы. Случайный лесной классификатор является примером ансамблевого классификатора.