Предсказание следующего в заданной входной последовательности — еще одна важная концепция в машинном обучении. В этой главе дается подробное объяснение анализа данных временных рядов.
Вступление
Данные временного ряда означают данные, которые находятся в последовательности определенных временных интервалов. Если мы хотим построить предсказание последовательности в машинном обучении, то нам приходится иметь дело с последовательными данными и временем. Данные серии — это резюме последовательных данных. Упорядочение данных является важной особенностью последовательных данных.
Основная концепция анализа последовательностей или анализа временных рядов
Анализ последовательности или анализ временных рядов предназначен для прогнозирования следующего в заданной входной последовательности на основе ранее наблюдавшегося. Предсказание может быть обо всем, что может быть следующим: символ, число, погода на следующий день, следующий термин в речи и т. Д. Анализ последовательности может быть очень полезен в таких приложениях, как анализ фондового рынка, прогнозирование погоды и рекомендации по продукту.
пример
Рассмотрим следующий пример, чтобы понять прогноз последовательности. Здесь A, B, C, D — заданные значения, и вы должны предсказать значение E, используя модель прогнозирования последовательности.
Установка полезных пакетов
Для анализа данных временных рядов с использованием Python нам необходимо установить следующие пакеты:
Панды
Pandas — это библиотека с открытым исходным кодом, имеющая лицензию BSD, которая обеспечивает высокую производительность, простоту использования структуры данных и инструменты анализа данных для Python. Вы можете установить Pandas с помощью следующей команды —
pip install pandas
Если вы используете Anaconda и хотите установить с помощью менеджера пакетов conda , вы можете использовать следующую команду:
conda install -c anaconda pandas
hmmlearn
Это BSD-библиотека с открытым исходным кодом, которая состоит из простых алгоритмов и моделей для изучения скрытых марковских моделей (HMM) в Python. Вы можете установить его с помощью следующей команды —
pip install hmmlearn
Если вы используете Anaconda и хотите установить с помощью менеджера пакетов conda , вы можете использовать следующую команду:
conda install -c omnia hmmlearn
PyStruct
Это структурированная библиотека обучения и прогнозирования. Алгоритмы обучения, реализованные в PyStruct, имеют такие имена, как условные случайные поля (CRF), марковские случайные сети с максимальным запасом (M3N) или машины опорных векторов структур. Вы можете установить его с помощью следующей команды —
pip install pystruct
CVXOPT
Используется для выпуклой оптимизации на основе языка программирования Python. Это также бесплатный программный пакет. Вы можете установить его с помощью следующей команды —
pip install cvxopt
Если вы используете Anaconda и хотите установить с помощью менеджера пакетов conda , вы можете использовать следующую команду:
conda install -c anaconda cvdoxt
Панды: обработка, нарезка и извлечение статистики из данных временных рядов
Панды — очень полезный инструмент, если вам приходится работать с данными временных рядов. С помощью панд вы можете выполнить следующее —
-
Создайте диапазон дат с помощью пакета pd.date_range
-
Индекс панды с датами с помощью пакета pd.Series
-
Выполните повторную выборку с помощью пакета ts.resample
-
Изменить частоту
Создайте диапазон дат с помощью пакета pd.date_range
Индекс панды с датами с помощью пакета pd.Series
Выполните повторную выборку с помощью пакета ts.resample
Изменить частоту
пример
В следующем примере показано, как обрабатывать и разрезать данные временных рядов с помощью Pandas. Обратите внимание, что здесь мы используем данные по месячным колебаниям в Арктике, которые можно загрузить с сайта month.ao.index.b50.current.ascii и которые мы можем преобразовать в текстовый формат.
Обработка данных временных рядов
Для обработки данных временных рядов вам необходимо выполнить следующие шаги:
Первый шаг включает в себя импорт следующих пакетов —
import numpy as np import matplotlib.pyplot as plt import pandas as pd
Затем определите функцию, которая будет считывать данные из входного файла, как показано в приведенном ниже коде —
def read_data(input_file): input_data = np.loadtxt(input_file, delimiter = None)
Теперь преобразуйте эти данные во временные ряды. Для этого создайте диапазон дат нашего временного ряда. В этом примере мы сохраняем один месяц как частоту данных. Наш файл содержит данные, которые начинаются с января 1950 года.
dates = pd.date_range('1950-01', periods = input_data.shape[0], freq = 'M')
На этом этапе мы создаем данные временных рядов с помощью Pandas Series, как показано ниже —
output = pd.Series(input_data[:, index], index = dates) return output if __name__=='__main__':
Введите путь к входному файлу, как показано здесь —
input_file = "/Users/admin/AO.txt"
Теперь преобразуйте столбец в формат временных рядов, как показано здесь —
timeseries = read_data(input_file)
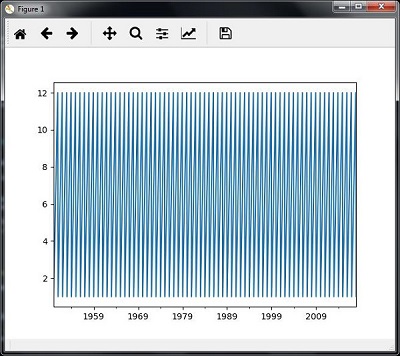
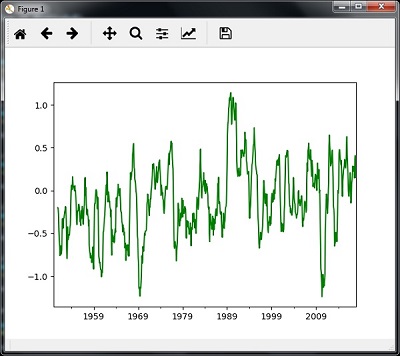
Наконец, нанесите на график и визуализируйте данные, используя показанные команды —
plt.figure() timeseries.plot() plt.show()
Вы увидите графики, как показано на следующих изображениях —
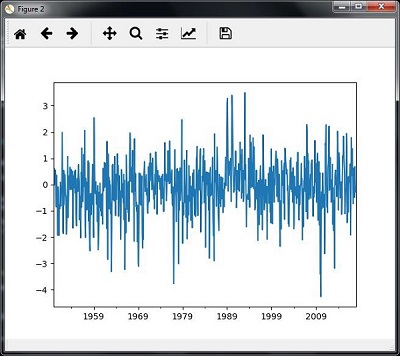
Нарезка данных временного ряда
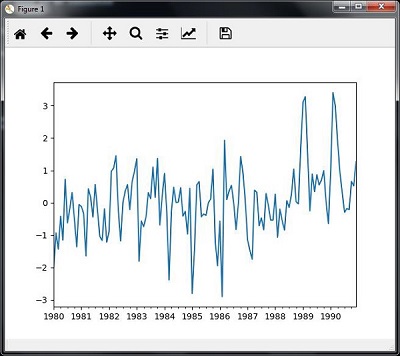
Разрезание включает в себя получение только некоторой части данных временного ряда. В качестве примера мы разбиваем данные только с 1980 по 1990 год. Обратите внимание на следующий код, который выполняет эту задачу:
timeseries['1980':'1990'].plot() <matplotlib.axes._subplots.AxesSubplot at 0xa0e4b00> plt.show()
Когда вы запускаете код для нарезки данных временных рядов, вы можете увидеть следующий график, как показано на рисунке здесь —
Извлечение статистики из данных временных рядов
Вам придется извлечь некоторую статистику из заданных данных, в случаях, когда вам нужно сделать какой-то важный вывод. Среднее, дисперсия, корреляция, максимальное значение и минимальное значение являются одними из таких статистических данных. Вы можете использовать следующий код, если вы хотите извлечь такую статистику из данных временных рядов —
Имею в виду
Вы можете использовать функцию mean () для нахождения среднего значения, как показано здесь:
timeseries.mean()
Тогда результат, который вы увидите в рассмотренном примере:
-0.11143128165238671
максимальная
Вы можете использовать функцию max () , чтобы найти максимум, как показано здесь —
timeseries.max()
Тогда результат, который вы увидите в рассмотренном примере:
3.4952999999999999
минимальный
Вы можете использовать функцию min (), чтобы найти минимум, как показано здесь —
timeseries.min()
Тогда результат, который вы увидите в рассмотренном примере:
-4.2656999999999998
Получать все сразу
Если вы хотите рассчитать всю статистику за раз, вы можете использовать функцию description (), как показано здесь —
timeseries.describe()
Тогда результат, который вы увидите в рассмотренном примере:
count 817.000000 mean -0.111431 std 1.003151 min -4.265700 25% -0.649430 50% -0.042744 75% 0.475720 max 3.495300 dtype: float64
Повторные выборки
Вы можете пересчитать данные с другой частотой. Два параметра для повторной выборки:
- Временной период
- метод
Повторная выборка со средним ()
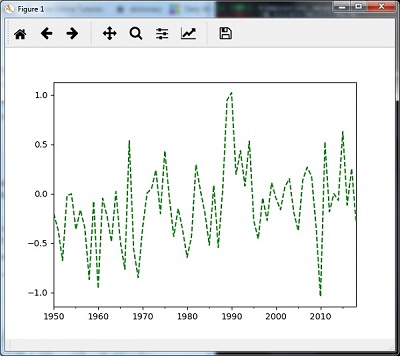
Вы можете использовать следующий код для повторной выборки данных с помощью метода mean (), который является методом по умолчанию —
timeseries_mm = timeseries.resample("A").mean() timeseries_mm.plot(style = 'g--') plt.show()
Затем вы можете наблюдать следующий график как результат передискретизации, используя mean () —
Повторная выборка с медианой ()
Вы можете использовать следующий код для повторной выборки данных, используя метод median () —
timeseries_mm = timeseries.resample("A").median()
timeseries_mm.plot()
plt.show()
Затем вы можете наблюдать следующий график как результат повторной выборки с помощью медианы () —
Скользящее среднее
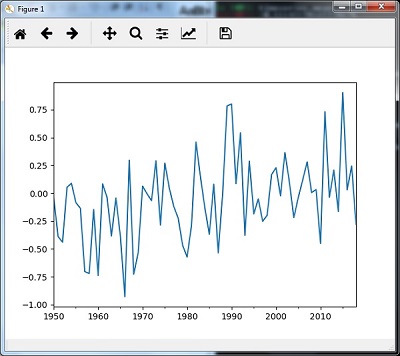
Вы можете использовать следующий код для расчета скользящего (скользящего) среднего значения —
timeseries.rolling(window = 12, center = False).mean().plot(style = '-g') plt.show()
Затем вы можете наблюдать следующий график как результат скользящего (скользящего) среднего значения —
Анализ последовательных данных по скрытой марковской модели (HMM)
HMM — это статистическая модель, которая широко используется для данных, имеющих продолжение и расширяемость, таких как анализ фондовых рынков временных рядов, проверка работоспособности и распознавание речи. В этом разделе подробно рассматривается анализ последовательных данных с использованием скрытой модели Маркова (HMM).
Скрытая Марковская Модель (HMM)
HMM — это стохастическая модель, построенная на концепции цепочки Маркова, основанной на предположении, что вероятность будущей статистики зависит только от текущего состояния процесса, а не от любого предшествующего ему состояния. Например, при подбрасывании монеты мы не можем сказать, что результатом пятого броска будет голова. Это связано с тем, что у монеты нет памяти, а следующий результат не зависит от предыдущего результата.
Математически HMM состоит из следующих переменных:
Штаты (S)
Это набор скрытых или скрытых состояний, присутствующих в HMM. Обозначается С.
Выходные символы (O)
Это набор возможных выходных символов, присутствующих в HMM. Обозначается О.
Матрица вероятности перехода состояния (A)
Это вероятность перехода из одного состояния в другое. Обозначается А.
Матрица вероятности выбросов наблюдений (B)
Это вероятность испускания / наблюдения символа в определенном состоянии. Обозначается Б.
Матрица априорной вероятности (Π)
Это вероятность запуска в определенном состоянии из различных состояний системы. Обозначается Π.
Следовательно, НММ может быть определен как ? = (S, O, A, B, ?) ,
где,
- S = {s 1 , s 2 ,…, s N } — это набор из N возможных состояний,
- O = {o 1 , o 2 ,…, o M } представляет собой набор из M возможных символов наблюдения,
- A является матрицей вероятности перехода состояния N?N (TPM),
- B — N observationM матрица наблюдения или вероятности выбросов (EPM),
- π — N-мерный вектор распределения вероятности начального состояния.
Пример: анализ данных фондового рынка
В этом примере мы будем шаг за шагом анализировать данные фондового рынка, чтобы получить представление о том, как HMM работает с данными последовательных или временных рядов. Обратите внимание, что мы реализуем этот пример на Python.
Импортируйте необходимые пакеты, как показано ниже —
import datetime import warnings
Теперь используйте данные фондового рынка из пакета matpotlib.finance , как показано здесь —
import numpy as np from matplotlib import cm, pyplot as plt from matplotlib.dates import YearLocator, MonthLocator try: from matplotlib.finance import quotes_historical_yahoo_och1 except ImportError: from matplotlib.finance import ( quotes_historical_yahoo as quotes_historical_yahoo_och1) from hmmlearn.hmm import GaussianHMM
Загрузите данные с даты начала и окончания, то есть между двумя конкретными датами, как показано здесь —
start_date = datetime.date(1995, 10, 10) end_date = datetime.date(2015, 4, 25) quotes = quotes_historical_yahoo_och1('INTC', start_date, end_date)
На этом этапе мы будем извлекать заключительные кавычки каждый день. Для этого используйте следующую команду —
closing_quotes = np.array([quote[2] for quote in quotes])
Теперь мы будем извлекать объем акций, торгуемых каждый день. Для этого используйте следующую команду —
volumes = np.array([quote[5] for quote in quotes])[1:]
Здесь, возьмите процентную разницу цен закрытия акций, используя код, показанный ниже —
diff_percentages = 100.0 * np.diff(closing_quotes) / closing_quotes[:-] dates = np.array([quote[0] for quote in quotes], dtype = np.int)[1:] training_data = np.column_stack([diff_percentages, volumes])
На этом этапе создайте и обучите гауссовский HMM. Для этого используйте следующий код —
hmm = GaussianHMM(n_components = 7, covariance_type = 'diag', n_iter = 1000) with warnings.catch_warnings(): warnings.simplefilter('ignore') hmm.fit(training_data)
Теперь сгенерируйте данные, используя модель HMM, используя показанные команды:
num_samples = 300 samples, _ = hmm.sample(num_samples)
Наконец, на этом этапе мы строим график и визуализируем разницу в процентах и объемах акций, торгуемых как выходные данные, в форме графика.
Используйте следующий код для построения и визуализации разницы в процентах —
plt.figure() plt.title('Difference percentages') plt.plot(np.arange(num_samples), samples[:, 0], c = 'black')
Используйте следующий код для построения графика и визуализации объема торгуемых акций.