Регрессия является одним из наиболее важных инструментов статистического и машинного обучения. Мы не ошибемся, если скажем, что путь машинного обучения начинается с регрессии. Его можно определить как параметрический метод, который позволяет нам принимать решения на основе данных или, другими словами, позволяет нам делать прогнозы на основе данных, изучая взаимосвязь между входными и выходными переменными. Здесь выходные переменные, зависящие от входных переменных, являются непрерывными действительными числами. В регрессии отношение между входными и выходными переменными имеет значение, и это помогает нам понять, как значение выходной переменной изменяется с изменением входной переменной. Регрессия часто используется для прогнозирования цен, экономики, изменений и так далее.
Построение регрессоров в Python
В этом разделе мы узнаем, как построить как регрессор с одним, так и с несколькими переменными.
Линейный регрессор / регрессор с одной переменной
Давайте отметим несколько необходимых пакетов —
import numpy as np from sklearn import linear_model import sklearn.metrics as sm import matplotlib.pyplot as plt
Теперь нам нужно предоставить входные данные, и мы сохранили наши данные в файле с именем linear.txt.
input = 'D:/ProgramData/linear.txt'
Нам нужно загрузить эти данные с помощью функции np.loadtxt .
input_data = np.loadtxt(input, delimiter=',') X, y = input_data[:, :-1], input_data[:, -1]
Следующим шагом будет обучение модели. Давайте дадим учебные и испытательные образцы.
training_samples = int(0.6 * len(X)) testing_samples = len(X) - num_training X_train, y_train = X[:training_samples], y[:training_samples] X_test, y_test = X[training_samples:], y[training_samples:]
Теперь нам нужно создать объект линейного регрессора.
reg_linear = linear_model.LinearRegression()
Тренируйте объект с обучающими образцами.
reg_linear.fit(X_train, y_train)
Нам нужно сделать прогноз с данными тестирования.
y_test_pred = reg_linear.predict(X_test)
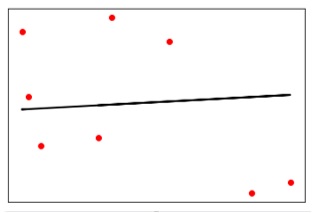
Теперь постройте и визуализируйте данные.
plt.scatter(X_test, y_test, color = 'red') plt.plot(X_test, y_test_pred, color = 'black', linewidth = 2) plt.xticks(()) plt.yticks(()) plt.show()
Выход
Теперь мы можем вычислить производительность нашей линейной регрессии следующим образом:
print("Performance of Linear regressor:") print("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2)) print("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2)) print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2)) print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2)) print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))
Выход
Производительность линейного регрессора —
Mean absolute error = 1.78 Mean squared error = 3.89 Median absolute error = 2.01 Explain variance score = -0.09 R2 score = -0.09
В приведенном выше коде мы использовали эти небольшие данные. Если вам нужен большой набор данных, вы можете использовать sklearn.dataset, чтобы импортировать больший набор данных.
2,4.82.9,4.72.5,53.2,5.56,57.6,43.2,0.92.9,1.92.4, 3.50.5,3.41,40.9,5.91.2,2.583.2,5.65.1,1.54.5, 1.22.3,6.32.1,2.8
Многовариантный регрессор
Во-первых, давайте импортируем несколько необходимых пакетов —
import numpy as np from sklearn import linear_model import sklearn.metrics as sm import matplotlib.pyplot as plt from sklearn.preprocessing import PolynomialFeatures
Теперь нам нужно предоставить входные данные, и мы сохранили наши данные в файле с именем linear.txt.
input = 'D:/ProgramData/Mul_linear.txt'
Мы загрузим эти данные с помощью функции np.loadtxt .
input_data = np.loadtxt(input, delimiter=',') X, y = input_data[:, :-1], input_data[:, -1]
Следующим шагом будет обучение модели; Мы дадим образцы для обучения и тестирования.
training_samples = int(0.6 * len(X)) testing_samples = len(X) - num_training X_train, y_train = X[:training_samples], y[:training_samples] X_test, y_test = X[training_samples:], y[training_samples:]
Теперь нам нужно создать объект линейного регрессора.
reg_linear_mul = linear_model.LinearRegression()
Тренируйте объект с обучающими образцами.
reg_linear_mul.fit(X_train, y_train)
Теперь, наконец, нам нужно сделать прогноз с данными тестирования.
y_test_pred = reg_linear_mul.predict(X_test)
print("Performance of Linear regressor:")
print("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))
Выход
Производительность линейного регрессора —
Mean absolute error = 0.6 Mean squared error = 0.65 Median absolute error = 0.41 Explain variance score = 0.34 R2 score = 0.33
Теперь мы создадим полином 10 степени и обучим регрессора. Мы предоставим образец данных.
polynomial = PolynomialFeatures(degree = 10) X_train_transformed = polynomial.fit_transform(X_train) datapoint = [[2.23, 1.35, 1.12]] poly_datapoint = polynomial.fit_transform(datapoint) poly_linear_model = linear_model.LinearRegression() poly_linear_model.fit(X_train_transformed, y_train) print("\nLinear regression:\n", reg_linear_mul.predict(datapoint)) print("\nPolynomial regression:\n", poly_linear_model.predict(poly_datapoint))
Выход
Линейная регрессия —
[2.40170462]
Полиномиальная регрессия —
[1.8697225]
В приведенном выше коде мы использовали эти небольшие данные. Если вам нужен большой набор данных, вы можете использовать sklearn.dataset, чтобы импортировать больший набор данных.