Что такое BFS?
BFS — это алгоритм, который используется для отображения данных, поиска в дереве или обходных структур. Алгоритм эффективно посещает и маркирует все ключевые узлы на графике в точном масштабе.
Этот алгоритм выбирает один узел (начальную или исходную точку) на графике и затем посещает все узлы, смежные с выбранным узлом. Когда алгоритм посещает и отмечает начальный узел, он движется к ближайшим не посещенным узлам и анализирует их.
После посещения все узлы помечаются. Эти итерации продолжаются до тех пор, пока все узлы графа не будут успешно посещены и отмечены. Полная форма BFS — поиск в ширину.
В этом ЧФ против. Учебник по двоичному дереву DFS, вы изучите:
- Что такое BFS?
- Что такое DFS?
- Пример БФС
- Пример ДФС
- Разница между BFS и DFS Binary Tree
- Приложения BFS
- Приложения DFS
Что такое DFS?
DFS — это алгоритм поиска или обхода графиков или деревьев в направлении глубины. Выполнение алгоритма начинается с корневого узла и исследует каждую ветвь перед возвратом. Он использует структуру данных стека для запоминания, получения последующей вершины и запуска поиска всякий раз, когда в любой итерации возникает тупик. Полная форма DFS — поиск в глубину.
Пример БФС
В следующем примере DFS мы использовали граф, имеющий 6 вершин.
Пример БФС
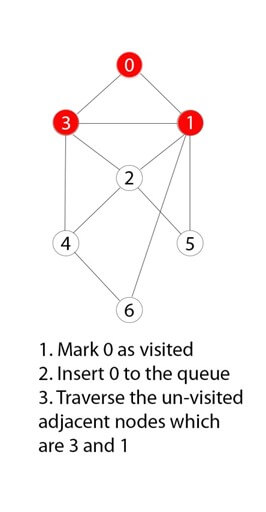
Шаг 1)
У вас есть график из семи чисел в диапазоне от 0 до 6.
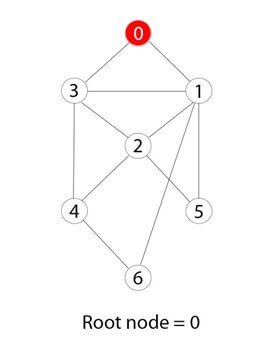
Шаг 2)
0 или ноль был отмечен как корневой узел.
Шаг 3)
0 посещается, помечается и вставляется в структуру данных очереди.
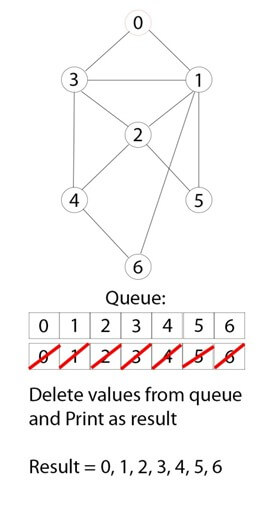
Шаг 4)
Оставшиеся 0 соседних и не посещенных узлов посещаются, помечаются и вставляются в очередь.
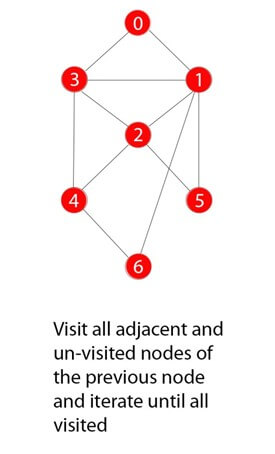
Шаг 5)
Итерации обхода повторяются до тех пор, пока не будут посещены все узлы.
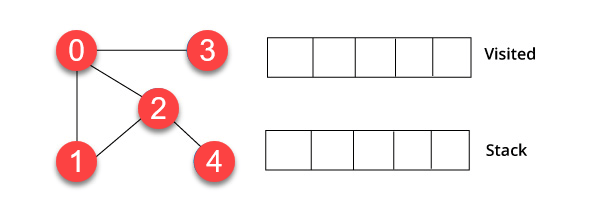
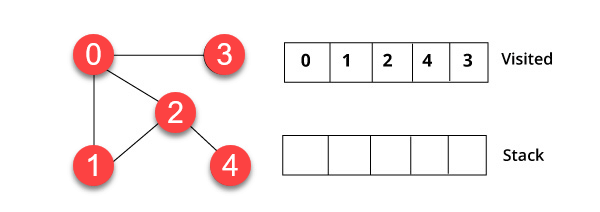
Пример ДФС
В следующем примере DFS мы использовали неориентированный граф с 5 вершинами.
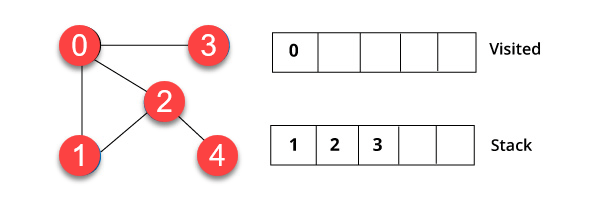
Шаг 1)
Мы начали с вершины 0. Алгоритм начинается с помещения его в список посещений и одновременного размещения всех смежных вершин в структуре данных, называемой стеком.
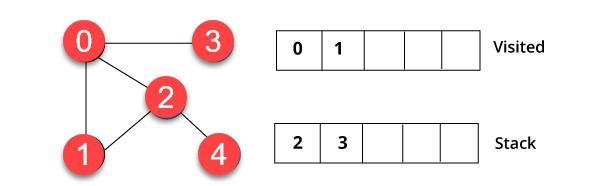
Шаг 2)
Вы посетите элемент, который находится вверху стека, например, 1, и перейдете к смежным узлам. Это потому, что 0 уже был посещен. Поэтому мы посещаем вершину 2.
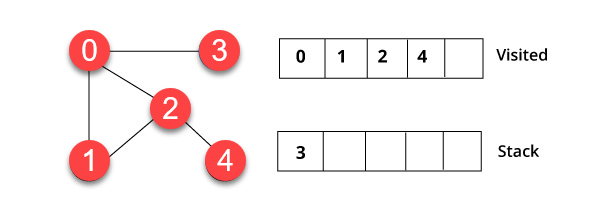
Шаг 3)
У вершины 2 есть соседняя не посещенная вершина в 4. Поэтому мы добавляем это в стек и посещаем его.
Шаг 4)
Наконец, мы посетим последнюю вершину 3, она не имеет никаких не посещенных соседних узлов. Мы завершили обход графа, используя алгоритм DFS.
Разница между BFS и DFS Binary Tree
| BFS | ДФС |
| BFS находит кратчайший путь к месту назначения. | DFS переходит в конец поддерева, а затем возвращается. |
| Полная форма BFS — поиск в ширину. | Полная форма DFS — поиск в глубину. |
| Он использует очередь для отслеживания следующего места для посещения. | Он использует стек для отслеживания следующего места для посещения. |
| BFS проходит в соответствии с уровнем дерева. | DFS проходит по глубине дерева. |
| Это реализовано с использованием списка FIFO. | Это реализовано с использованием списка LIFO. |
| Это требует больше памяти по сравнению с DFS. | Это требует меньше памяти по сравнению с BFS. |
| Этот алгоритм дает решение с минимальным путем. | Этот алгоритм не гарантирует решения с минимальным путем. |
| В BFS нет необходимости возвращаться назад. | В DFS есть необходимость возврата. |
| Вы никогда не сможете попасть в ловушку конечных циклов. | Вы можете попасть в бесконечные петли. |
| Если вы не нашли никакой цели, вам может потребоваться расширить множество узлов до того, как решение будет найдено. | Если вы не найдете никакой цели, может произойти откат конечного узла. |
Приложения BFS
Вот приложения BFS:
Невзвешенные графики:
Алгоритм BFS может легко создать кратчайший путь и минимальное остовное дерево для посещения всех вершин графа в кратчайшие сроки с высокой точностью.
P2P-сети:
BFS может быть реализован для определения местоположения всех ближайших или соседних узлов в одноранговой сети. Это позволит найти необходимые данные быстрее.
Веб-сканеры:
Поисковые системы или веб-сканеры могут легко создавать индексы нескольких уровней, используя BFS. Реализация BFS начинается с источника, который является веб-страницей, а затем посещает все ссылки из этого источника.
Сетевое вещание:
Широковещательный пакет управляется алгоритмом BFS, чтобы найти и добраться до всех узлов, для которых он имеет адрес.
Приложения DFS
Вот важные приложения DFS:
Взвешенный график:
В взвешенном графе обход по графу DFS генерирует дерево кратчайшего пути и минимальное остовное дерево.
Обнаружение цикла на графике:
Граф имеет цикл, если мы нашли задний край во время DFS. Таким образом, мы должны запустить DFS для графа и проверить для задних ребер.
Найти путь:
Мы можем специализироваться на алгоритме DFS для поиска пути между двумя вершинами.
Топологическая сортировка:
Он в основном используется для планирования заданий из заданных зависимостей в группе заданий. В информатике он используется при планировании команд, сериализации данных, логическом синтезе, определении порядка выполнения задач компиляции.
Поиск сильно связанных компонентов графика:
Он используется в графе DFS, когда есть путь от каждой вершины графа до других оставшихся вершин.
Решение головоломок только с одним решением:
Алгоритм DFS может быть легко адаптирован для поиска всех решений лабиринта путем включения узлов в существующий путь в посещаемый набор.
ОСНОВНЫЕ РАЗЛИЧИЯ:
- BFS находит кратчайший путь к месту назначения, тогда как DFS идет в конец поддерева, а затем возвращается.
- Полная форма BFS — поиск в ширину, а полная форма DFS — поиск в глубину.
- BFS использует очередь для отслеживания следующего места для посещения. тогда как DFS использует стек для отслеживания следующего места для посещения.
- BFS проходит в соответствии с уровнем дерева, в то время как DFS проходит в соответствии с глубиной дерева.
- BFS реализована с использованием списка FIFO, с другой стороны, DFS реализована с использованием списка LIFO.
- В BFS вы никогда не попадете в конечные циклы, тогда как в DFS вы можете попасть в бесконечные циклы.