Что такое жадный алгоритм?
В GREEDY ALGORITHM набор ресурсов рекурсивно разделяется на основе максимальной, немедленной доступности этого ресурса на любом этапе выполнения.
Чтобы решить проблему, основанную на жадном подходе, есть два этапа
- сканирование списка предметов
- оптимизация.
Эти этапы выполняются параллельно по ходу деления массива.
Чтобы понять жадный подход, вам нужно иметь практические знания рекурсии и переключения контекста. Это поможет вам понять, как отслеживать код. Вы можете определить жадную парадигму с точки зрения ваших собственных необходимых и достаточных утверждений.
Два условия определяют жадную парадигму.
- Каждое поэтапное решение должно структурировать проблему в направлении ее наиболее приемлемого решения.
- Достаточно, если структурирование проблемы может остановиться за конечное число жадных шагов.
Продолжив теоретизирование, давайте опишем историю, связанную с жадным подходом.
В этом уроке Greedy вы узнаете:
- История жадных алгоритмов
- Жадные стратегии и решения
- Характеристики жадного подхода
- Зачем использовать жадный подход?
- Как решить проблему выбора активности
- Архитектура Жадного подхода
- Недостатки жадных алгоритмов
История жадных алгоритмов
Вот важный ориентир жадных алгоритмов:
- Жадные алгоритмы были концептуализированы для многих алгоритмов обхода графов в 1950-х годах.
- Эсдгер Джикстра концептуализировал алгоритм для генерации минимальных остовных деревьев. Он стремился сократить количество маршрутов в столице Нидерландов Амстердаме.
- В том же десятилетии Prim и Kruskal разработали стратегии оптимизации, основанные на минимизации затрат на пути по взвешенным маршрутам.
- В 70-х годах американские исследователи, Cormen, Rivest и Stein, предложили рекурсивную подструктуризацию жадных решений в своем классическом введении в книгу алгоритмов.
- Жадная парадигма была зарегистрирована как стратегия оптимизации другого типа в записях NIST в 2005 году.
- До сегодняшнего дня протоколы, которые работают в сети, такие как OSPF и многие другие сетевые протоколы коммутации пакетов, используют жадную стратегию, чтобы минимизировать время, затрачиваемое в сети.
Жадные стратегии и решения
Логика в ее самой простой форме сводилась к «жадному» или «не жадному». Эти утверждения были определены подходом, принятым для продвижения на каждой стадии алгоритма.
Например, алгоритм Джикстра использовал пошаговую жадную стратегию, идентифицирующую хосты в Интернете путем вычисления функции стоимости. Значение, возвращаемое функцией стоимости, определяет, является ли следующий путь «жадным» или «не жадным».
Короче говоря, алгоритм перестает быть жадным, если на любом этапе он делает шаг, который не является локально жадным. Проблема останавливается без дальнейшего охвата жадности.
Характеристики жадного подхода
Важными характеристиками жадного метода являются:
- Существует упорядоченный список ресурсов с указанием стоимости или стоимости. Эти количественные ограничения на систему.
- Вы возьмете максимальное количество ресурсов за время применения ограничения.
- Например, в задаче планирования операций стоимость ресурсов указывается в часах, и действия должны выполняться в последовательном порядке.
Зачем использовать жадный подход?
Вот причины использования жадного подхода:
- У жадного подхода есть несколько компромиссов, которые могут сделать его пригодным для оптимизации.
- Одна из важных причин состоит в том, чтобы немедленно найти наиболее выполнимое решение. В задаче выбора действий (поясняется ниже), если до завершения текущего действия можно выполнить больше действий, эти действия могут быть выполнены в одно и то же время.
- Другая причина заключается в рекурсивном разделении проблемы на основе условия без необходимости объединения всех решений.
- В задаче выбора действий шаг «рекурсивное разделение» достигается путем сканирования списка элементов только один раз и рассмотрения определенных действий.
Как решить проблему выбора активности
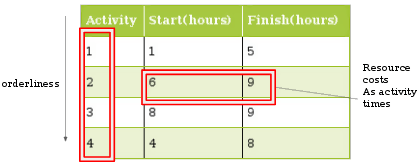
В примере планирования действий есть время «начала» и «окончания» для каждого действия. Каждое мероприятие индексируется номером для справки. Есть две категории деятельности.
- рассматриваемая деятельность : это деятельность, которая является ссылкой, с помощью которой анализируется способность выполнять более одной оставшейся деятельности.
- оставшиеся действия: действия по одному или нескольким показателям перед рассматриваемой деятельностью.
Общая продолжительность дает стоимость выполнения действия. То есть (финиш — старт) дает нам длительность как стоимость деятельности.
Вы узнаете, что жадная степень — это количество оставшихся действий, которые вы можете выполнить во время рассматриваемой деятельности.
Архитектура Жадного подхода
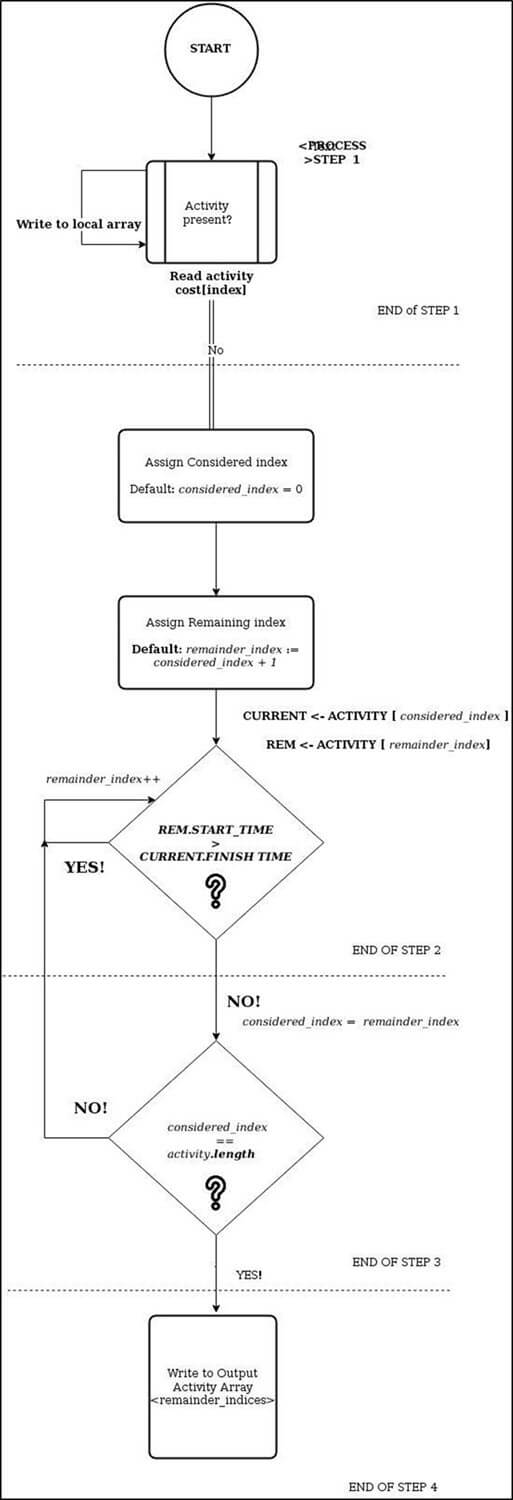
ШАГ 1)
Сканирование списка затрат на деятельность, начиная с индекса 0 в качестве рассматриваемого индекса.
ШАГ 2)
Когда к тому времени может быть завершено больше действий, рассматриваемая операция заканчивается, начните поиск одного или нескольких оставшихся действий.
ШАГ 3)
Если оставшихся действий больше нет, текущее оставшееся действие становится следующим рассматриваемым действием. Повторите шаги 1 и 2 для новой рассматриваемой операции. Если не осталось никаких действий, перейдите к шагу 4.
ШАГ 4)
Вернуть объединение рассмотренных индексов. Это индексы активности, которые будут использоваться для максимизации пропускной способности.
Код Объяснение
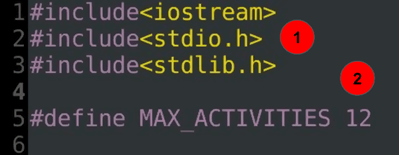
#include<iostream> #include<stdio.h> #include<stdlib.h> #define MAX_ACTIVITIES 12
Объяснение кода:
- Включенные заголовочные файлы / классы
- Максимальное количество действий, предоставляемых пользователем.
using namespace std;
class TIME
{
public:
int hours;
public: TIME()
{
hours = 0;
}
};
Объяснение кода:
- Пространство имен для потоковых операций.
- Определение класса для ВРЕМЕНИ
- Часовая метка.
- ВРЕМЯ конструктор по умолчанию
- Переменная часов.
class Activity
{
public:
int index;
TIME start;
TIME finish;
public: Activity()
{
start = finish = TIME();
}
};
Объяснение кода:
- Определение класса из деятельности
- Отметки времени, определяющие продолжительность
- Все метки времени инициализируются в 0 в конструкторе по умолчанию
class Scheduler
{
public:
int considered_index,init_index;
Activity *current_activities = new Activity[MAX_ACTIVITIES];
Activity *scheduled;
Объяснение кода:
- Часть 1 определения класса планировщика.
- Рассматриваемый индекс является отправной точкой для сканирования массива.
- Индекс инициализации используется для назначения случайных меток времени.
- Массив объектов деятельности динамически размещается с помощью оператора new.
- Запланированный указатель определяет текущее базовое местоположение для жадности.
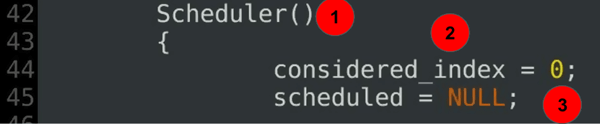
Scheduler()
{
considered_index = 0;
scheduled = NULL;
...
...
Объяснение кода:
- Конструктор планировщика — часть 2 определения класса планировщика.
- Рассматриваемый индекс определяет текущее начало текущего сканирования.
- Текущий жадный экстент не определен в начале.
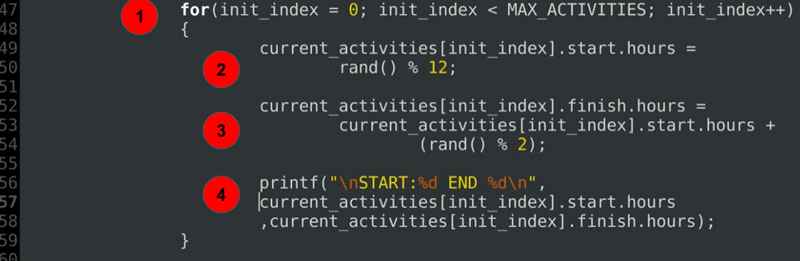
for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++)
{
current_activities[init_index].start.hours =
rand() % 12;
current_activities[init_index].finish.hours =
current_activities[init_index].start.hours +
(rand() % 2);
printf("\nSTART:%d END %d\n",
current_activities[init_index].start.hours
,current_activities[init_index].finish.hours);
}
…
…
Объяснение кода:
- Цикл for для инициализации начальных и конечных часов каждого из запланированных на данный момент действий.
- Начальная инициализация времени.
- Инициализация времени окончания всегда после или точно в начальный час.
- Оператор отладки для распечатки выделенных длительностей.
public: Activity * activity_select(int); };
Объяснение кода:
- Часть 4 — последняя часть определения класса планировщика.
- Функция выбора активности берет индекс начальной точки в качестве основы и делит жадный квест на жадные подзадачи.
Activity * Scheduler :: activity_select(int considered_index)
{
this->considered_index = considered_index;
int greedy_extent = this->considered_index + 1;
…
…
- Используя оператор разрешения области (: :), предоставляется определение функции.
- Рассматриваемый индекс — это индекс, называемый по значению. Greedy_extent — это инициализированный индекс после рассматриваемого индекса.
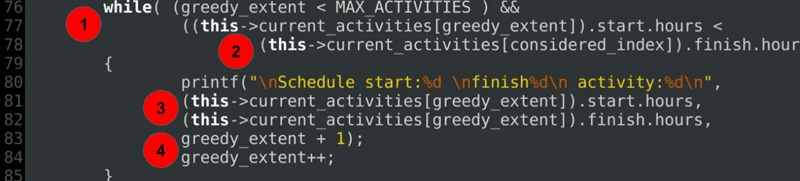
Activity * Scheduler :: activity_select(int considered_index)
{
while( (greedy_extent < MAX_ACTIVITIES ) &&
((this->current_activities[greedy_extent]).start.hours <
(this->current_activities[considered_index]).finish.hours ))
{
printf("\nSchedule start:%d \nfinish%d\n activity:%d\n",
(this->current_activities[greedy_extent]).start.hours,
(this->current_activities[greedy_extent]).finish.hours,
greedy_extent + 1);
greedy_extent++;
}
…
...
Объяснение кода:
- Основная логика — жадная степень ограничена количеством действий.
- Время начала текущей деятельности проверяется как планируемое до того, как завершится рассматриваемая деятельность (заданная с помощью рассматриваемого индекса).
- Пока это возможно, печатается дополнительный оператор отладки.
- Переход к следующему индексу в массиве активности
...
if ( greedy_extent <= MAX_ACTIVITIES )
{
return activity_select(greedy_extent);
}
else
{
return NULL;
}
}
Объяснение кода:
- Условные проверки, если все действия были покрыты.
- Если нет, вы можете перезапустить своего жадного с рассматриваемым индексом в качестве текущей точки. Это рекурсивный шаг, который жадно разделяет формулировку задачи.
- Если да, он возвращается к вызывающей стороне без возможности расширения жадности.
int main()
{
Scheduler *activity_sched = new Scheduler();
activity_sched->scheduled = activity_sched->activity_select(
activity_sched->considered_index);
return 0;
}
Объяснение кода:
- Основная функция, используемая для вызова планировщика.
- Новый планировщик создается.
- Функция выбора действия, которая возвращает указатель типа действия, возвращается вызывающей стороне после того, как жадный квест закончен.
Вывод:
START:7 END 7 START:9 END 10 START:5 END 6 START:10 END 10 START:9 END 10 Schedule start:5 finish6 activity:3 Schedule start:9 finish10 activity:5
Недостатки жадных алгоритмов
Он не подходит для задач, где решение требуется для каждой подзадачи, такой как сортировка.
В таких проблемах жадная стратегия может быть неправильной; в худшем случае даже приведет к неоптимальному решению.
Поэтому недостатком жадных алгоритмов является использование незнания того, что стоит перед текущим жадным состоянием.
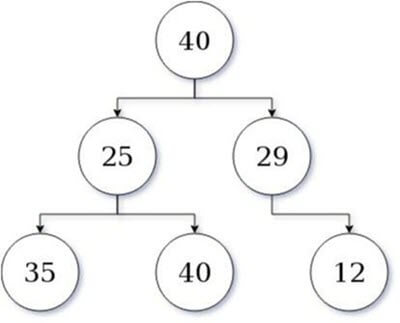
Ниже приведено описание недостатка жадного подхода.
В жадном сканировании, показанном здесь в виде дерева (более высокое значение — более высокая жадность), состояние алгоритма со значением 40 скорее всего примет 29 в качестве следующего значения. Кроме того, его квест заканчивается на 12. Это составляет значение 41.
Однако, если алгоритм выбрал неоптимальный путь или принял стратегию завоевания. затем за 25 последует 40, и общее улучшение затрат составит 65, что оценивается на 24 пункта выше как неоптимальное решение.
Примеры жадных алгоритмов
Большинство сетевых алгоритмов используют жадный подход. Вот список немногих из них —
- Алгоритм минимального связующего дерева Прима
- Задача коммивояжера
- График — раскраска карты
- Алгоритм минимального связующего дерева Крускала
- Алгоритм минимального связующего дерева Дейкстры
- Graph — Vertex Cover
- Рюкзак Проблема
- Проблема планирования работы
Резюме:
Подводя итог, статья определила жадную парадигму, показала, как жадная оптимизация и рекурсия могут помочь вам получить наилучшее решение до определенного момента. Пример выбора деятельности был описан как стратегическая проблема, которая могла бы достичь максимальной пропускной способности, используя жадный подход. В конце были объяснены недостатки использования жадного подхода.