Учебники

7) Двоичное дерево поиска

Сентябрь 28, 2019

В этом уроке по структуре данных вы узнаете:

Атрибуты бинарного дерева поиска

BST состоит из нескольких узлов и состоит из следующих атрибутов:

  • Узлы дерева представлены в родительско-дочерних отношениях
  • Каждый родительский узел может иметь ноль дочерних узлов или максимум два подузла или поддерева слева и справа.
  • Каждое поддерево, также известное как двоичное дерево поиска, имеет подветвия справа и слева от себя.
  • Все узлы связаны парами ключ-значение.
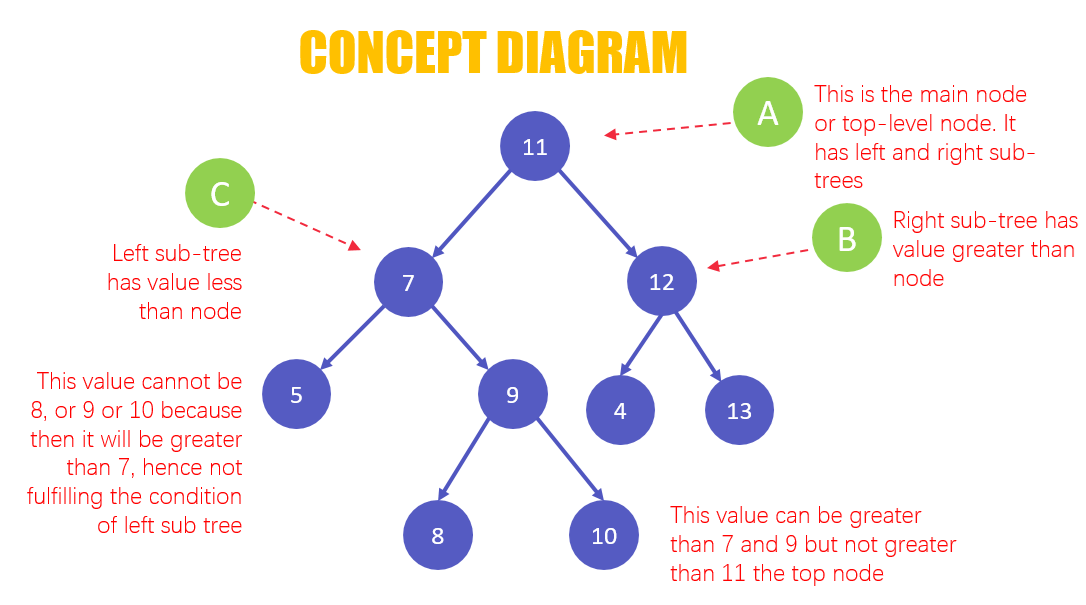
  • Ключи узлов, присутствующих в левом поддереве, меньше, чем ключи их родительского узла.
  • Аналогично, ключи левых узлов поддерева имеют меньшие значения, чем ключи их родительских узлов.

  1. Существует главный узел или родительский уровень 11. Под ним находятся левый и правый узлы / ветви со своими собственными значениями ключей.
  2. Правое поддерево имеет значения ключа больше, чем родительский узел
  3. Левое поддерево имеет значения, чем родительский узел

Зачем нам нужно дерево двоичного поиска?

  • Двумя основными факторами, которые делают бинарное дерево поиска оптимальным решением любых реальных проблем, являются Скорость и Точность.
  • Из-за того, что бинарный поиск имеет ветвистый формат с отношениями родитель-потомок, алгоритм знает, в каком месте дерева нужно искать элементы. Это уменьшает количество сравнений ключ-значение, которые должна выполнить программа, чтобы найти нужный элемент.
  • Кроме того, в случае, если элемент для поиска больше или меньше, чем родительский узел, узел знает, какую сторону дерева искать. Причина в том, что левое поддерево всегда меньше родительского узла, а правое поддерево имеет значения, всегда равные или превышающие родительский узел.
  • BST обычно используется для реализации сложного поиска, надежной игровой логики, операций автозавершения и графики.
  • Алгоритм эффективно поддерживает такие операции, как поиск, вставка и удаление.

Типы бинарных деревьев

Три вида бинарных деревьев:

  • Полное двоичное дерево: все уровни в деревьях полны возможных исключений последнего уровня. Точно так же все узлы заполнены, направляя крайний левый.
  • Полное двоичное дерево: все узлы имеют 2 дочерних узла, кроме листа.
  • Сбалансированное или совершенное двоичное дерево: в дереве все узлы имеют двух дочерних элементов. Кроме того, уровень каждого подузла одинаковый.

Как работает дерево бинарного поиска?

Дерево всегда имеет корневой узел и дополнительные дочерние узлы, слева или справа. Алгоритм выполняет все операции, сравнивая значения с корневым и его дальнейшими дочерними узлами в левом или правом поддереве соответственно.

Зависит от того, какой элемент будет вставлен, найден или удален, после сравнения алгоритм может легко удалить левое или правое поддерево корневого узла.

BST в первую очередь предлагает следующие три типа операций для вашего использования:

  • Поиск: поиск элемента из двоичного дерева
  • Вставить: добавляет элемент в двоичное дерево
  • Удалить: удалить элемент из двоичного дерева

Каждая операция имеет свою структуру и метод выполнения / анализа, но наиболее сложной из них является операция удаления.

Операция поиска

Всегда инициируйте анализ дерева в корневом узле, а затем двигайтесь дальше к правому или левому поддереву корневого узла, в зависимости от того, какой элемент должен быть меньше или больше корневого.

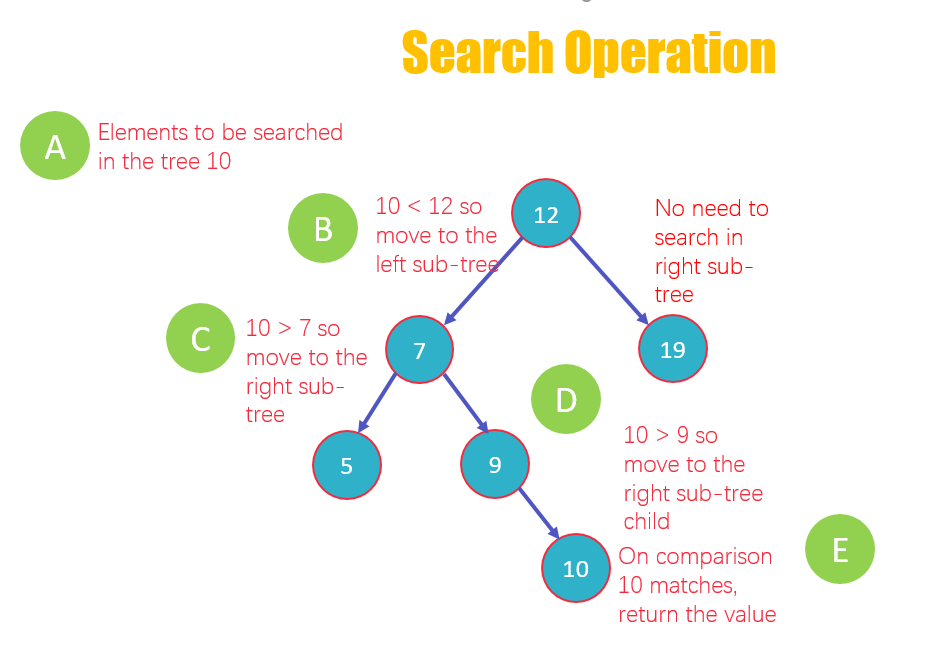
  1. Элемент для поиска — 10
  2. Сравните элемент с корневым узлом 12, 10 <12, следовательно, вы переместитесь в левое поддерево. Не нужно анализировать правильное поддерево
  3. Теперь сравните 10 с узлом 7, 10> 7, поэтому перейдите к правому поддереву
  4. Затем сравните 10 со следующим узлом, который является 9, 10> 9, посмотрите в дочернем поддереве справа
  5. 10 соответствует значению в узле, 10 = 10, возвращает значение пользователю.

Операция вставки

Это очень прямолинейная операция. Сначала вставляется корневой узел, затем сравнивается следующее значение с корневым узлом. Если значение больше корневого, оно добавляется к правому поддереву, а если оно меньше корневого, оно добавляется к левому поддереву.

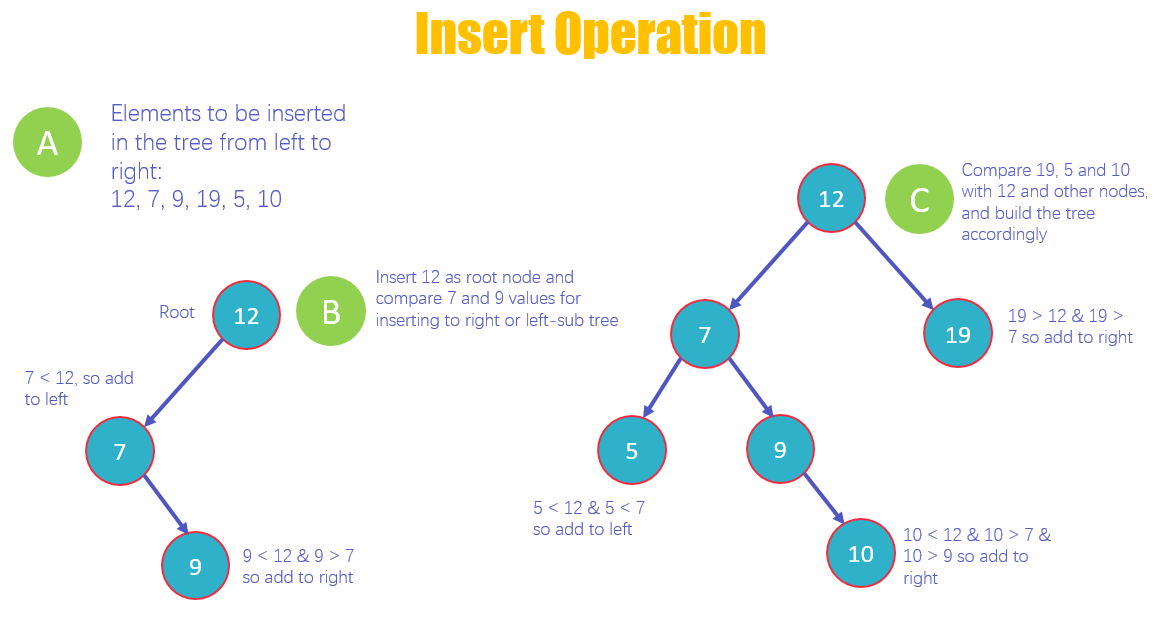
  1. Существует список из 6 элементов, которые необходимо вставить в BST по порядку слева направо
  2. Вставьте 12 в качестве корневого узла и сравните следующие значения 7 и 9 для вставки соответственно в правое и левое поддерево.
  3. Сравните остальные значения 19, 5 и 10 с корневым узлом 12 и разместите их соответствующим образом. 19> 12 поместите его как правого ребенка 12, 5 <12 и 5 <7, следовательно, поместите его как левого ребенка 7 лет.
    1. Теперь сравните 10, 10 — это <12, а 10 -> 7 и 10 -> 9, поместите 10 как правильное поддерево 9.

Операции удаления

Удалить является наиболее продвинутым и сложным среди всех других операций. В BST обрабатывается несколько дел.

  • Случай 1 — Узел с нулевыми дочерними элементами: это самая простая ситуация, вам просто нужно удалить узел, у которого больше нет дочерних элементов справа или слева.
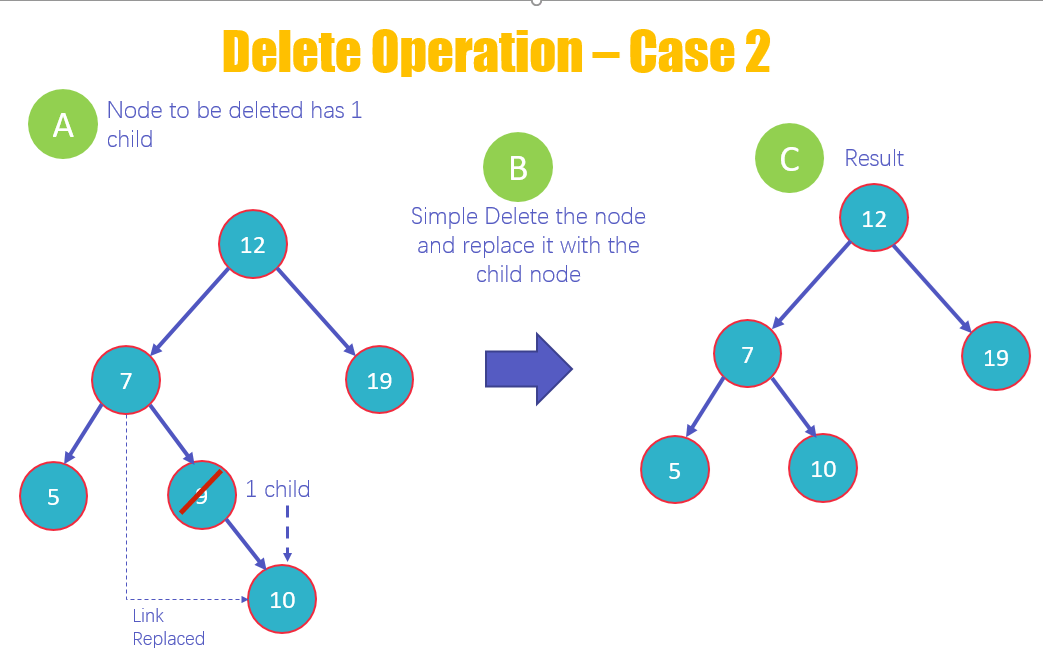
  • Случай 2 — Узел с одним дочерним узлом: после удаления узла просто подключите его дочерний узел с родительским узлом удаленного значения.
  • Пример 3 Узел с двумя детьми: это самая сложная ситуация, и она работает по следующим двум правилам
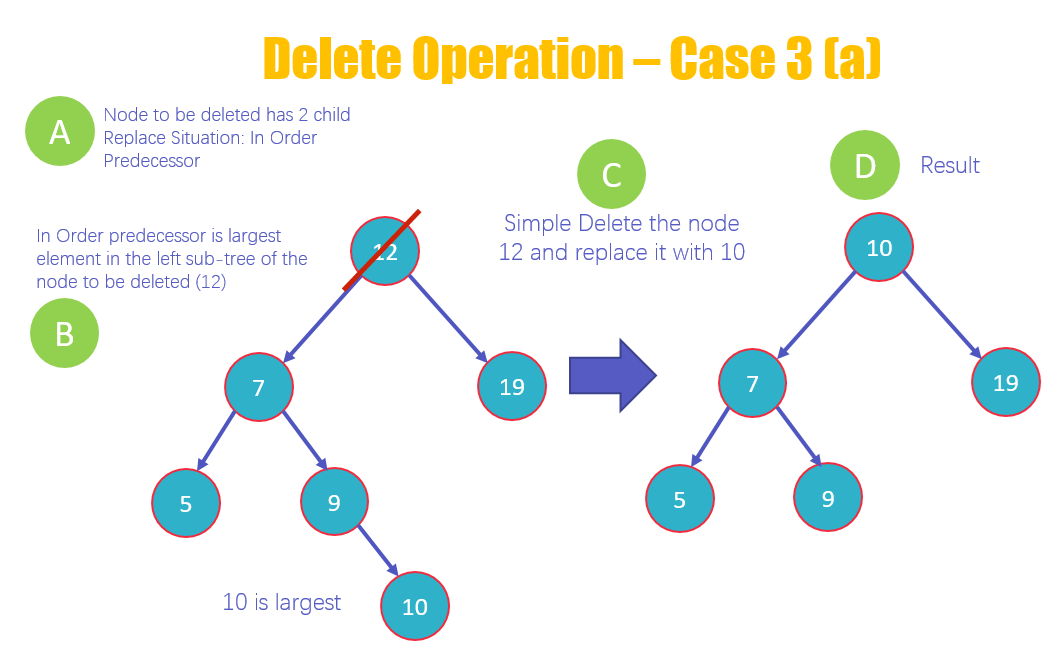
    • 3a — В Предшественнике заказа: вам нужно удалить узел с двумя дочерними элементами и заменить его наибольшим значением в левом поддереве удаленного узла.
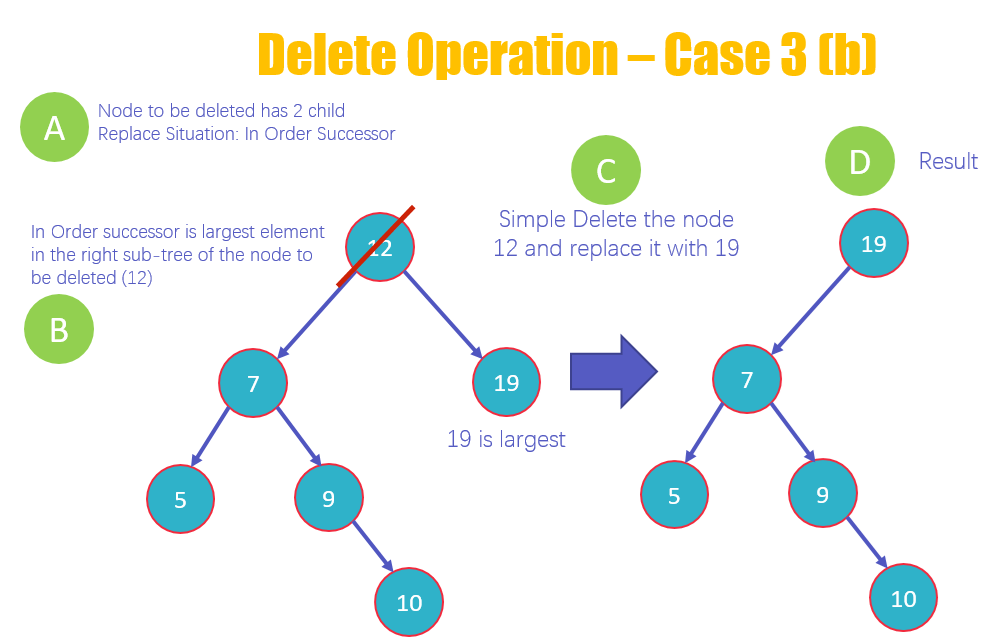
    • 3b — В порядке преемника: необходимо удалить узел с двумя дочерними элементами и заменить его наибольшим значением в правом поддереве удаленного узла

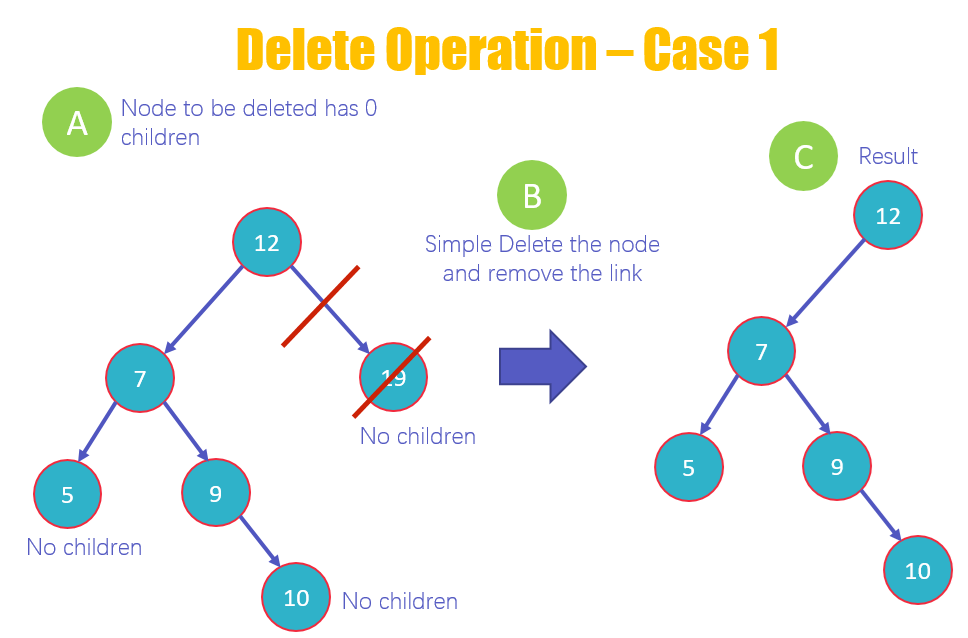
  1. Это первый случай удаления, при котором вы удаляете узел, у которого нет дочерних элементов. Как видно из диаграммы, 19, 10 и 5 не имеют детей. Но мы удалим 19.
  2. Удалите значение 19 и удалите ссылку из узла.
  3. Посмотреть новую структуру BST без 19

  1. Это второй случай удаления, при котором вы удаляете узел, у которого есть 1 дочерний элемент, как вы можете видеть на диаграмме, что у 9 есть один дочерний элемент.
  2. Удалите узел 9, замените его дочерним 10 и добавьте ссылку с 7 на 10.
  3. Посмотреть новую структуру BST без 9

  1. Здесь вы будете удалять узел 12, который имеет двух детей
  2. Удаление узла будет происходить на основе правила предшественника по порядку, что означает, что его заменит самый большой элемент в левом поддереве из 12.
  3. Удалите узел 12 и замените его на 10, так как это наибольшее значение в левом поддереве.
  4. Просмотр новой структуры BST после удаления 12

  1. 1 Удалите узел 12 с двумя дочерними элементами.
  2. 2 Удаление узла будет происходить на основе правила преемника по порядку, что означает, что его заменит самый большой элемент в правом поддереве из 12
  3. 3 Удалите узел 12 и замените его на 19, так как это наибольшее значение в правом поддереве.
  4. 4 Просмотр новой структуры BST после удаления 12

Важные условия

  • Вставить — вставляет элемент в дерево / создает дерево.
  • Поиск — поиск элемента в дереве.
  • Preorder Traversal — обход дерева по предзаказу.
  • Inorder Traversal — обход дерева по порядку.
  • Postorder Traversal — обход дерева по порядку заказа.

Резюме

  • BST — это алгоритм продвинутого уровня, который выполняет различные операции на основе сравнения значений узлов с корневым узлом.
  • Любая из точек в иерархии родитель-потомок представляет узел. По крайней мере один родительский или корневой узел остается постоянно.
  • Есть левое поддерево и правое поддерево. Левое поддерево содержит значения, которые меньше корневого узла. Однако правое поддерево содержит значение, которое больше корневого узла.
  • Каждый узел может иметь ноль, одного или двух дочерних элементов.
  • Двоичное дерево поиска облегчает основные операции, такие как поиск, вставка и удаление.
  • У удаления, являющегося наиболее сложным, есть несколько случаев, например, узел без дочернего элемента, узел с одним дочерним элементом и узел с двумя дочерними элементами.
  • Алгоритм используется в реальных решениях, таких как игры, автозаполнение данных и графика.

 

49
Share: