Учебники

6) Алгоритм BFS

Сентябрь 28, 2019

Что такое алгоритм BFS (поиск в ширину)?

Поиск в ширину (BFS) — это алгоритм, который используется для отображения данных или поиска в дереве или структурах обхода. Полная форма BFS — поиск в ширину.

Алгоритм эффективно посещает и маркирует все ключевые узлы на графике в точном масштабе. Этот алгоритм выбирает один узел (начальную или исходную точку) на графике и затем посещает все узлы, смежные с выбранным узлом. Помните, что BFS обращается к этим узлам один за другим.

Когда алгоритм посещает и отмечает начальный узел, он движется к ближайшим не посещенным узлам и анализирует их. После посещения все узлы помечаются. Эти итерации продолжаются до тех пор, пока все узлы графа не будут успешно посещены и отмечены.

В этом руководстве вы узнаете:

Что такое обход графиков?

Обход графа является широко используемой методологией для определения местоположения вершины в графе. Это расширенный алгоритм поиска, который может анализировать график со скоростью и точностью наряду с маркировкой последовательности посещенных вершин. Этот процесс позволяет вам быстро посещать каждый узел на графике, не будучи заблокированным в бесконечном цикле.

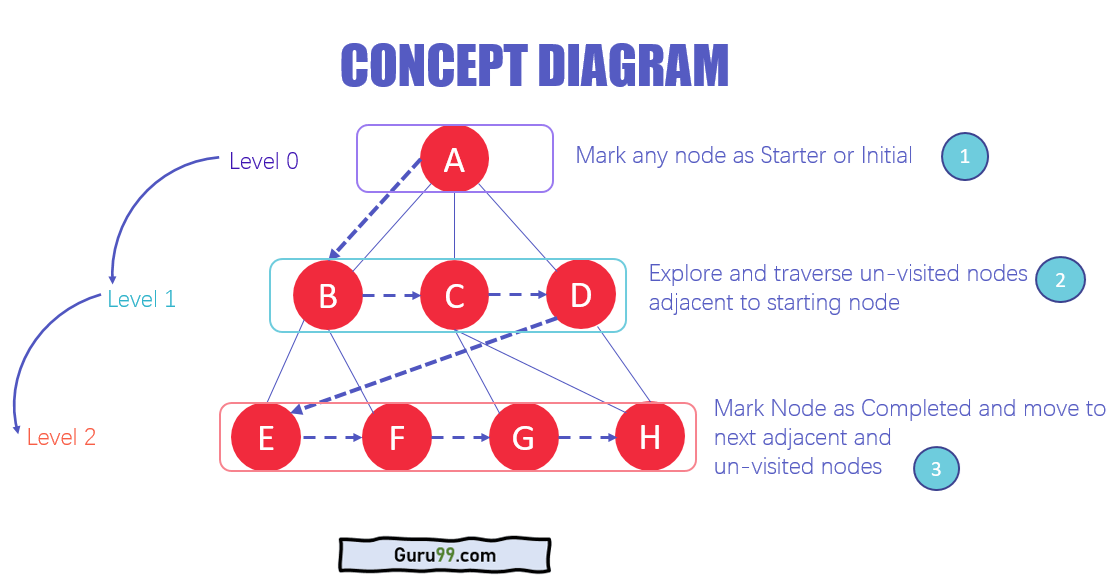
Архитектура алгоритма BFS

  1. На разных уровнях данных вы можете пометить любой узел как начальный или начальный узел, чтобы начать обход. BFS посетит узел и пометит его как посещенный и поместит в очередь.
  2. Теперь BFS посетит ближайшие и непосещенные узлы и пометит их. Эти значения также добавляются в очередь. Очередь работает по модели FIFO.
  3. Аналогичным образом оставшиеся ближайшие и не посещенные узлы на графике анализируются, помечаются и добавляются в очередь. Эти элементы удаляются из очереди как полученные и распечатываются как результат.

Зачем нам нужен алгоритм BFS?

Существует множество причин использовать алгоритм BFS для поиска в наборе данных. Вот некоторые из наиболее важных аспектов, которые делают этот алгоритм вашим первым выбором:

  • BFS полезен для анализа узлов в графе и построения кратчайшего пути прохождения через них.
  • BFS может проходить через граф за наименьшее количество итераций.
  • Архитектура алгоритма BFS проста и надежна.
  • Результат алгоритма BFS имеет высокий уровень точности по сравнению с другими алгоритмами.
  • Итерации BFS являются бесшовными, и нет никакой вероятности того, что этот алгоритм попадет в проблему бесконечного цикла.

Как работает алгоритм BFS?

Обход графа требует, чтобы алгоритм посещал, проверял и / или обновлял каждый не посещаемый узел в древовидной структуре. Обход графа классифицируется по порядку, в котором они посещают узлы на графе.

Алгоритм BFS запускает операцию с первого или начального узла в графе и тщательно ее обходит. Как только он успешно проходит начальный узел, следующая непересекающаяся вершина в графе посещается и отмечается.

Следовательно, вы можете сказать, что все узлы, смежные с текущей вершиной, посещены и пройдены в первой итерации. Простая методология очереди используется для реализации работы алгоритма BFS и состоит из следующих шагов:

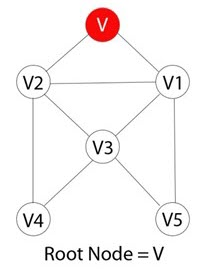
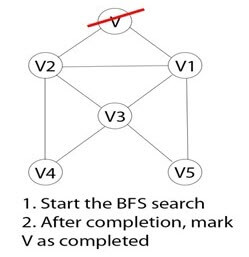
Шаг 1)

Каждая вершина или узел в графе известна. Например, вы можете пометить узел как V.

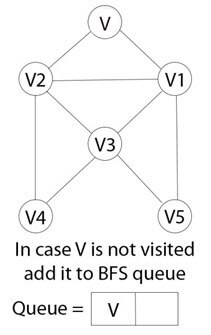
Шаг 2)

Если к вершине V нет доступа, добавьте вершину V в очередь BFS.

Шаг 3)

Запустите поиск BFS и после завершения отметьте вершину V как посещенную.

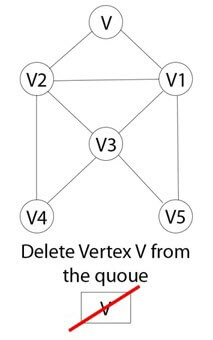
Шаг 4)

Очередь BFS все еще не пуста, поэтому удалите вершину V графа из очереди.

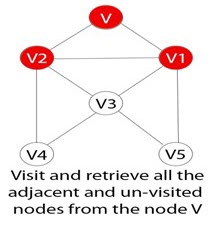
Шаг 5)

Получить все остальные вершины графа, которые смежны с вершиной V

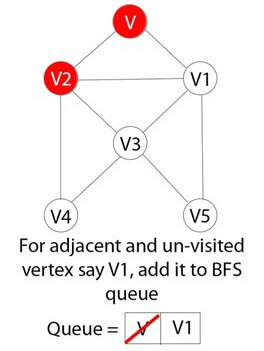
Шаг 6)

Например, для каждой смежной вершины V1, если она еще не посещена, добавьте V1 в очередь BFS.

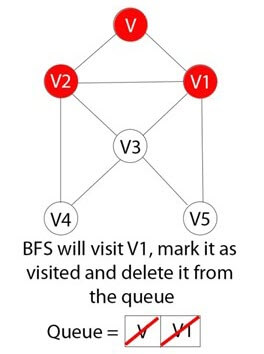
Шаг 7)

BFS посетит V1 и пометит его как посещенный и удалит его из очереди.

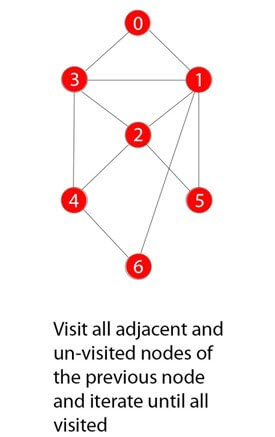
Пример алгоритма BFS

Шаг 1)

У вас есть график из семи чисел в диапазоне от 0 до 6.

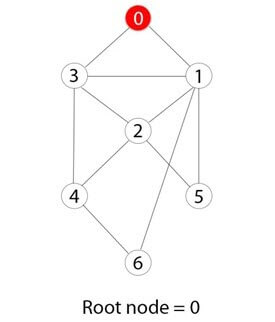
Шаг 2)

0 или ноль был отмечен как корневой узел.

Шаг 3)

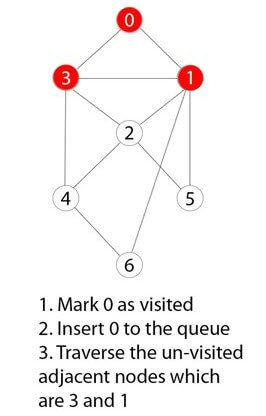
0 посещается, помечается и вставляется в структуру данных очереди.

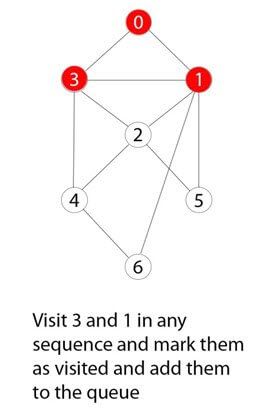
Шаг 4)

Оставшиеся 0 соседних и не посещенных узлов посещаются, помечаются и вставляются в очередь.

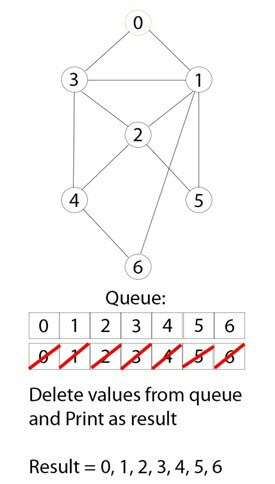
Шаг 5)

Итерации обхода повторяются до тех пор, пока не будут посещены все узлы.

Правила алгоритма BFS

Вот важные правила использования алгоритма BFS:

  • Структура данных очереди (FIFO-First in First Out) используется BFS.
  • Вы помечаете любой узел в графе как корневой и начинаете проходить через него данные.
  • BFS пересекает все узлы на графике и продолжает отбрасывать их как завершенные.
  • BFS посещает соседний не посещаемый узел, помечает его как выполненный и вставляет в очередь.
  • Удаляет предыдущую вершину из очереди, если соседняя вершина не найдена.
  • Алгоритм BFS выполняет итерацию до тех пор, пока все вершины графа не пройдут успешно и не будут помечены как завершенные.
  • Нет циклов, вызванных BFS при прохождении данных с любого узла.

Применение алгоритма BFS

Давайте посмотрим на некоторые из реальных приложений, где реализация алгоритма BFS может быть очень эффективной.

  • Невзвешенные графы. Алгоритм BFS может легко создать кратчайший путь и минимальное остовное дерево для посещения всех вершин графа в кратчайшие сроки с высокой точностью.
  • P2P-сети: BFS может быть реализована для определения местоположения всех ближайших или соседних узлов в одноранговой сети. Это позволит найти необходимые данные быстрее.
  • Веб- сканеры : поисковые системы или веб-сканеры могут легко создавать индексы нескольких уровней, используя BFS. Реализация BFS начинается с источника, который является веб-страницей, а затем посещает все ссылки из этого источника.
  • Навигационные системы: BFS может помочь найти все соседние местоположения из основного или исходного местоположения.
  • Сетевое вещание: широковещательный пакет управляется алгоритмом BFS, чтобы найти и достичь всех узлов, для которых он имеет адрес.

Резюме

  • Обход графа — это уникальный процесс, который требует, чтобы алгоритм посещал, проверял и / или обновлял каждый отдельный узел в древовидной структуре. Алгоритм BFS работает по схожему принципу.
  • Алгоритм полезен для анализа узлов в графе и построения кратчайшего пути прохождения через них.
  • Алгоритм пересекает график за наименьшее количество итераций и за максимально короткое время.
  • BFS выбирает один узел (начальную или исходную точку) на графике, а затем посещает все узлы, смежные с выбранным узлом. BFS обращается к этим узлам один за другим.
  • Посещенные и помеченные данные помещаются в очередь BFS. Очередь работает в порядке очереди. Следовательно, элемент, помещенный в граф сначала, удаляется первым и печатается в результате.
  • Алгоритм BFS никогда не попадет в бесконечный цикл.
  • Благодаря высокой точности и надежной реализации, BFS используется во многих реальных решениях, таких как P2P-сети, веб-сканеры и сетевое вещание.

 

53
Share: