Что такое дерево B +?
В + Дерево в основном используется для реализации динамического индексирования на нескольких уровнях. По сравнению с B-Tree B + Tree хранит указатели данных только в конечных узлах дерева, что делает поиск более точным и быстрым.
Из этого урока B + Tree вы узнаете:
- Что такое дерево B +?
- Правила для B + Tree
- Зачем использовать B + Tree
- B + Дерево против B Дерево
- Операция поиска
- Операция вставки
- Удалить операцию
Правила для B + Tree
Вот основные правила для B + Tree.
- Листья используются для хранения записей данных.
- Хранится во внутренних узлах Дерева.
- Если значение целевого ключа меньше внутреннего узла, то следует точка только с левой стороны.
- Если значение целевого ключа больше или равно внутреннему узлу, то следует точка только справа от него.
- Корень имеет минимум двух детей.
Зачем использовать B + Tree
Вот причины использования B + Tree:
- Ключ в основном используется, чтобы помочь в поиске, направляя на соответствующий лист.
- B + Tree использует «коэффициент заполнения» для управления увеличением и уменьшением дерева.
- В деревьях B + многочисленные ключи могут быть легко размещены на странице памяти, поскольку у них нет данных, связанных с внутренними узлами. Следовательно, он быстро получит доступ к данным дерева, которые находятся на конечном узле.
- Комплексное полное сканирование всех элементов представляет собой дерево, для которого требуется всего один линейный проход, поскольку все конечные узлы дерева B + связаны друг с другом.
B + Дерево против B Дерево
Вот основные различия между B + Tree и B Tree
| B + Дерево | B Дерево |
| Поиск ключей можно повторить. | Ключи поиска не могут быть лишними. |
| Данные сохраняются только на конечных узлах. | Как конечные, так и внутренние узлы могут хранить данные |
| Данные, хранящиеся на конечном узле, делают поиск более точным и быстрым. | Поиск идет медленно из-за данных, хранящихся на листе и внутренних узлах. |
| Удаление не сложно, так как элемент удаляется только из конечного узла. | Удаление элементов — сложный и трудоемкий процесс. |
| Связанные конечные узлы делают поиск эффективным и быстрым. | Вы не можете связать конечные узлы. |
Операция поиска
В B + Tree поиск является одной из самых простых процедур для выполнения и получения быстрых и точных результатов.
Применим следующий алгоритм поиска:
- Чтобы найти нужную запись, необходимо выполнить бинарный поиск по доступным записям в дереве.
- В случае точного совпадения с ключом поиска соответствующая запись возвращается пользователю.
- Если точный ключ не найден в результате поиска в родительском, текущем или конечном узле, пользователю отображается «не найденное сообщение».
- Процесс поиска можно перезапустить для получения более точных результатов.
Алгоритм операции поиска
1. Call the binary search method on the records in the B+ Tree.
2. If the search parameters match the exact key
The accurate result is returned and displayed to the user
Else, if the node being searched is the current and the exact key is not found by the algorithm
Display the statement "Recordset cannot be found."
Выход :
Соответствующая запись, установленная для точного ключа, отображается пользователю; в противном случае неудачная попытка показывается пользователю.
Операция вставки
Следующий алгоритм применим для операции вставки:
- 50 процентов элементов в узлах перемещаются на новый лист для хранения.
- Родитель нового листа точно связан с минимальным значением ключа и новым местоположением в дереве.
- Разделите родительский узел на несколько мест, если он полностью используется.
- Теперь для лучших результатов центральная клавиша связана с узлом верхнего уровня этого листа.
- Пока узел верхнего уровня не найден, продолжайте повторять процесс, описанный в предыдущих шагах.
Вставить алгоритм работы
1. Even inserting at-least 1 entry into the leaf container does not make it full then add the record
2. Else, divide the node into more locations to fit more records.
a. Assign a new leaf and transfer 50 percent of the node elements to a new placement in the tree
b. The minimum key of the binary tree leaf and its new key address are associated with the top-level node.
c. Divide the top-level node if it gets full of keys and addresses.
i. Similarly, insert a key in the center of the top-level node in the hierarchy of the Tree.
d. Continue to execute the above steps until a top-level node is found that does not need to be divided anymore.
3) Build a new top-level root node of 1 Key and 2 indicators.
Выход :
Алгоритм определит элемент и успешно вставит его в требуемый конечный узел.
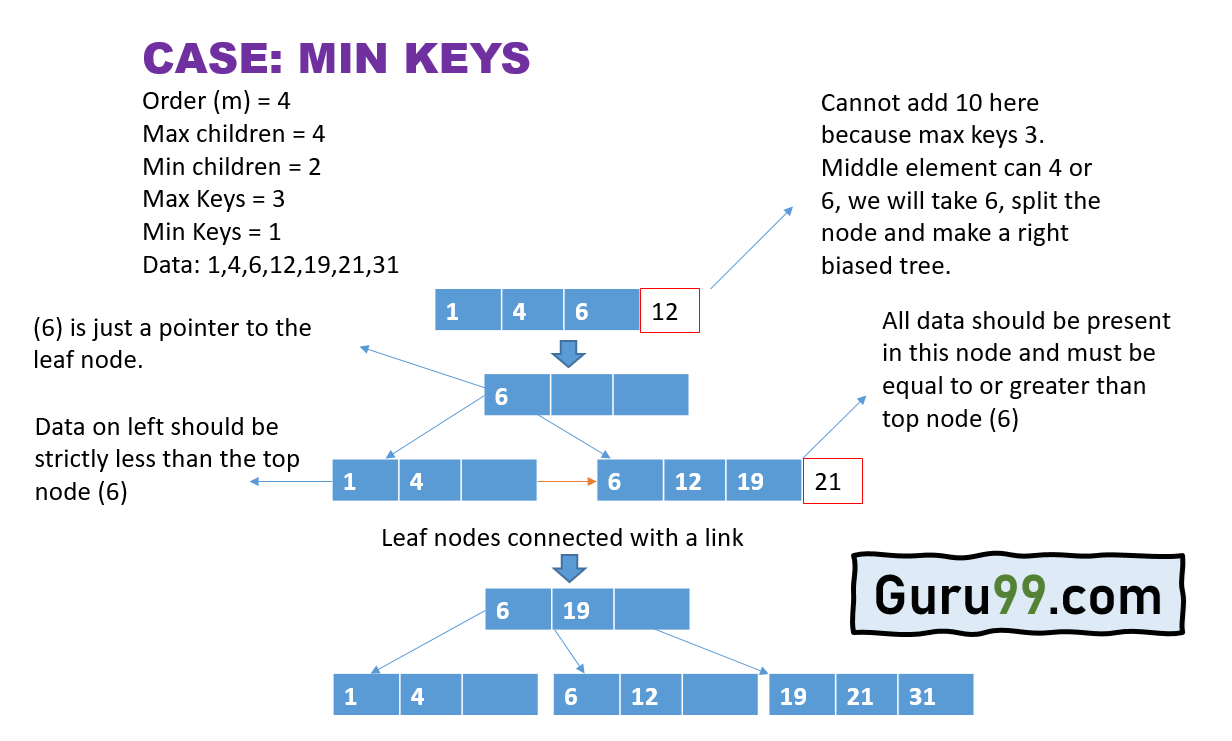
Приведенный выше пример примера B + Tree объясняется в следующих шагах:
- Во-первых, у нас есть 3 узла, и первые 3 элемента, а именно 1, 4 и 6, добавляются в соответствующие места в узлах.
- Следующее значение в ряду данных — 12, которое необходимо сделать частью дерева.
- Для этого разделите узел, добавьте 6 в качестве элемента указателя.
- Теперь создается правая иерархия дерева, и оставшиеся значения данных корректируются соответствующим образом с учетом применимых правил, равных или превышающих значения для узлов ключ-значение справа.
Удалить операцию
Сложность процедуры удаления в дереве B + превосходит сложность функций вставки и поиска.
Следующий алгоритм применим при удалении элемента из дерева B +:
- Во-первых, нам нужно найти листовую запись в дереве, содержащую ключ и указатель. удалите запись листа из дерева, если лист удовлетворяет точным условиям удаления записи.
- Если листовой узел удовлетворяет только удовлетворительному коэффициенту наполовину, операция завершается; в противном случае конечный узел имеет минимальное количество записей и не может быть удален.
- Другие связанные узлы справа и слева могут освободить любые записи, а затем переместить их на лист. Если эти критерии не выполняются, тогда они должны объединить конечный узел и связанный с ним узел в иерархии дерева.
- При объединении конечного узла со своими соседями справа или слева записи значений в конечном узле или связанном соседе, указывающие на узел верхнего уровня, удаляются.
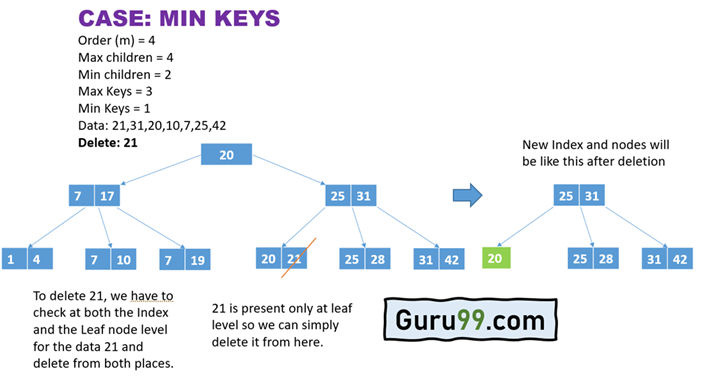
Приведенный выше пример иллюстрирует процедуру удаления элемента из дерева B + определенного порядка.
- Во-первых, точное местоположение удаляемого элемента определяется в дереве.
- Здесь удаляемый элемент может быть точно идентифицирован только на уровне листа, а не на месте размещения индекса. Следовательно, элемент может быть удален, не затрагивая правила удаления, что является значением минимального ключа.
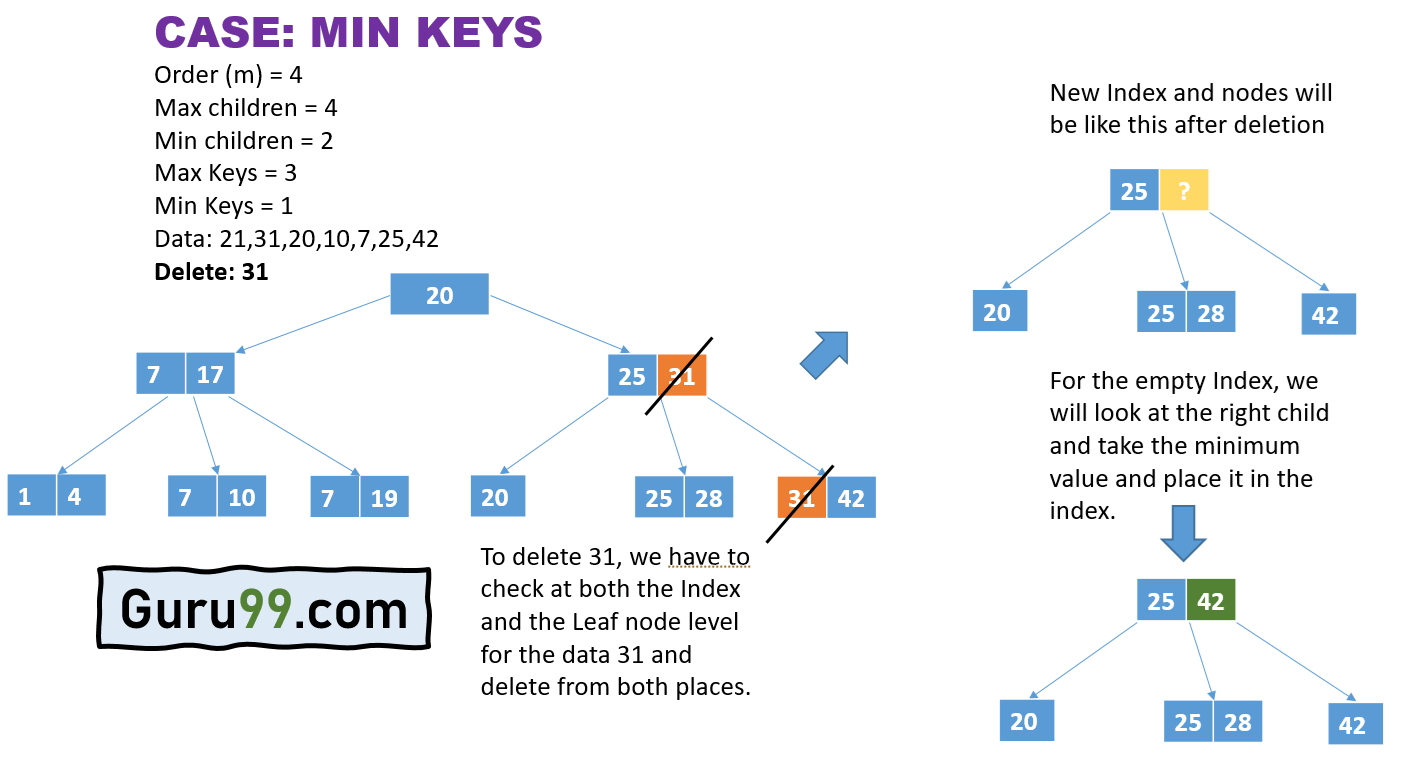
- В приведенном выше примере мы должны удалить 31 из дерева.
- Нам нужно найти экземпляры 31 в Index и Leaf.
- Мы видим, что 31 доступен как на уровне индекса, так и на уровне конечного узла. Следовательно, мы удаляем его из обоих экземпляров.
- Но мы должны заполнить индекс, указывающий на 42. Теперь мы рассмотрим правильного потомка младше 25 лет, возьмем минимальное значение и поместим его в качестве индекса. Таким образом, 42, являющееся единственным присутствующим значением, станет индексом.
Удалить алгоритм работы
1) Start at the root and go up to leaf node containing the key K
2) Find the node n on the path from the root to the leaf node containing K
A. If n is root, remove K
a. if root has more than one key, done
b. if root has only K
i) if any of its child nodes can lend a node
Borrow key from the child and adjust child links
ii) Otherwise merge the children nodes. It will be a new root
c. If n is an internal node, remove K
i) If n has at least ceil(m/2) keys, done!
ii) If n has less than ceil(m/2) keys,
If a sibling can lend a key,
Borrow key from the sibling and adjust keys in n and the parent node
Adjust child links
Else
Merge n with its sibling
Adjust child links
d. If n is a leaf node, remove K
i) If n has at least ceil(M/2) elements, done!
In case the smallest key is deleted, push up the next key
ii) If n has less than ceil(m/2) elements
If the sibling can lend a key
Borrow key from a sibling and adjust keys in n and its parent node
Else
Merge n and its sibling
Adjust keys in the parent node
Выход :
Ключ «K» удален, а ключи заимствованы у братьев и сестер для корректировки значений в n и его родительских узлах, если это необходимо.
Резюме:
- B + Tree — это самобалансирующаяся структура данных для точного и быстрого поиска, вставки и удаления данных.
- Мы можем легко получить полные или частичные данные, потому что прохождение через связанную древовидную структуру делает ее эффективной.
- Древовидная структура B + растет и уменьшается с увеличением / уменьшением количества хранимых записей.
- Хранение данных на конечных узлах и последующее разветвление внутренних узлов, очевидно, сокращает высоту дерева, что уменьшает операции ввода и вывода диска, в конечном итоге занимая гораздо меньше места на устройствах хранения.