Что такое B-дерево?
B Tree — это самобалансирующаяся структура данных, основанная на определенном наборе правил для поиска, вставки и удаления данных более быстрым и эффективным способом памяти. Чтобы достичь этого, для создания B-дерева следуйте следующим правилам.
B-дерево — это особый вид дерева в структуре данных. В 1972 году этот метод был впервые представлен McCreight, и Bayer назвал его m-way Search Tree с сбалансированной высотой. Это помогает сохранить отсортированные данные и позволяет выполнять различные операции, такие как вставка, поиск и удаление, за меньшее время.
В этом уроке B-Tree вы узнаете:
- Что такое B-дерево?
- Зачем использовать B-Tree
- История B Tree
- Операция поиска
- Операция вставки
- Удалить операцию
Правила для B-Tree
Здесь важны правила создания B_Tree
- Все листья будут созданы на одном уровне.
- B-Tree определяется числом степеней, которые также называют «порядком» (указанным внешним субъектом, например, программистом), называемым
m
и далее. Значение
m
зависит от размера блока на диске, на котором в первую очередь располагаются данные.
- Левое поддерево узла будет иметь меньшие значения, чем правая сторона поддерева. Это означает, что узлы также сортируются в порядке возрастания слева направо.
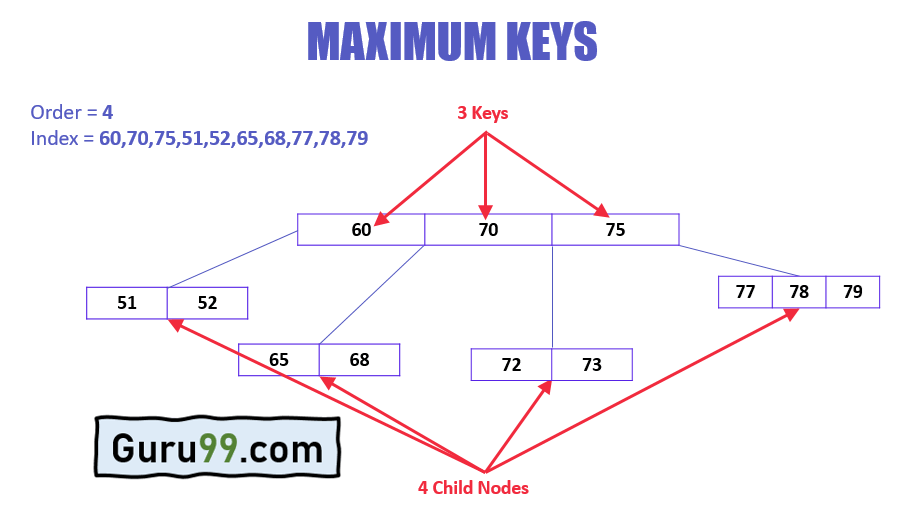
- Максимальное количество дочерних узлов, которые может содержать корневой узел, а также его дочерние узлы, рассчитывается по следующей формуле:
m – 1
Например:
m = 4 max keys: 4 – 1 = 3
- Каждый узел, кроме root, должен содержать минимальные ключи
[m/2]-1
Например:
m = 4 min keys: 4/2-1 = 1
- Максимальное количество дочерних узлов, которое может иметь узел, равно его степени, которая равна
m
- Минимальное число дочерних элементов, которое может иметь узел, составляет половину порядка, то есть m / 2 (берется значение потолка).
- Все ключи в узле отсортированы в порядке возрастания.
Зачем использовать B-Tree
Вот причины использования B-Tree
- Уменьшает количество операций чтения на диске
- B Деревья могут быть легко оптимизированы для настройки их размера (то есть количества дочерних узлов) в соответствии с размером диска.
- Это специально разработанный метод для обработки большого количества данных.
- Это полезный алгоритм для баз данных и файловых систем.
- Хороший выбор для чтения и записи больших блоков данных.
История B Tree
- Данные хранятся на диске в блоках, эти данные, когда заносятся в основную память (или ОЗУ), называются структурой данных.
- В случае больших данных поиск одной записи на диске требует чтения всего диска; это увеличивает время и потребление основной памяти из-за высокой частоты доступа к диску и размера данных.
- Чтобы преодолеть это, создаются индексные таблицы, которые сохраняют ссылки на записи на основе блоков, в которых они находятся. Это значительно сокращает время и потребление памяти.
- Поскольку у нас огромные данные, мы можем создавать многоуровневые индексные таблицы.
- Многоуровневый индекс может быть разработан с использованием B Tree для сохранения сортировки данных в режиме самобалансировки.
Операция поиска
Операция поиска является самой простой операцией на B Tree.
Применяется следующий алгоритм:
- Пусть ключ (значение) будет искать «k».
- Начните поиск с корня и рекурсивно пройдите вниз.
- Если k меньше корневого значения, ищите левое поддерево, если k больше корневого значения, ищите правое поддерево.
- Если узел имеет найденное k, просто верните узел.
- Если k не найдено в узле, перейдите к дочернему элементу с большим ключом.
- Если k не найдено в дереве, мы возвращаем NULL.
Операция вставки
Поскольку B Tree является самобалансирующимся деревом, вы не можете принудительно вставить ключ в любой узел.
Применяется следующий алгоритм:
- Запустите операцию поиска и найдите подходящее место для вставки.
- Вставьте новый ключ в нужное место, но если у узла уже есть максимальное количество ключей:
- Узел вместе с новым вставленным ключом будет отделен от среднего элемента.
- Средний элемент станет родительским для двух других дочерних узлов.
- Узлы должны переставлять ключи в порядке возрастания.
|
ПОДСКАЗКА |
Следующее неверно в отношении алгоритма вставки: Поскольку узел заполнен, поэтому он будет разделен, а затем будет вставлено новое значение |
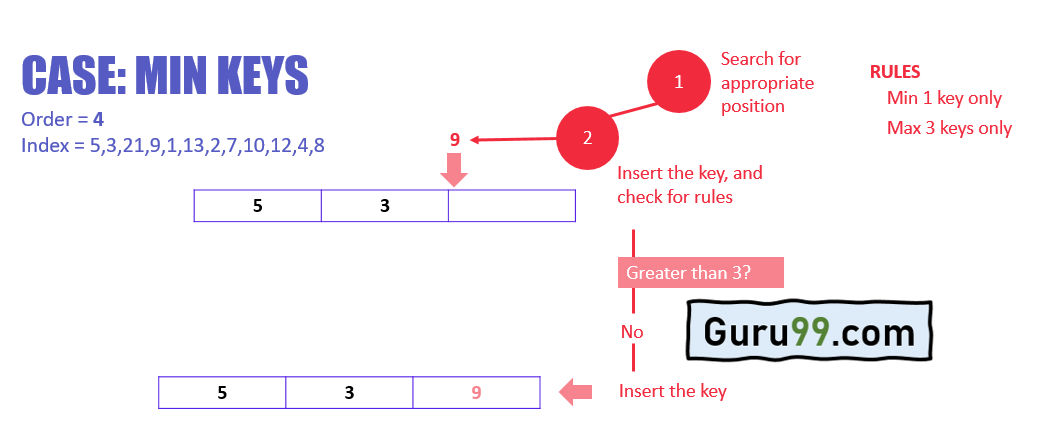
В приведенном выше примере:
- Поиск соответствующей позиции в узле для ключа
- Вставьте ключ в целевой узел и проверьте правила
- После вставки имеет ли узел более чем равный минимальному количеству ключей, которое равно 1? В этом случае, да, это так. Проверьте следующее правило.
- После вставки, у узла есть больше чем максимальное количество ключей, которое является 3? В этом случае нет, это не так. Это означает, что B-дерево не нарушает никаких правил, и вставка завершена.
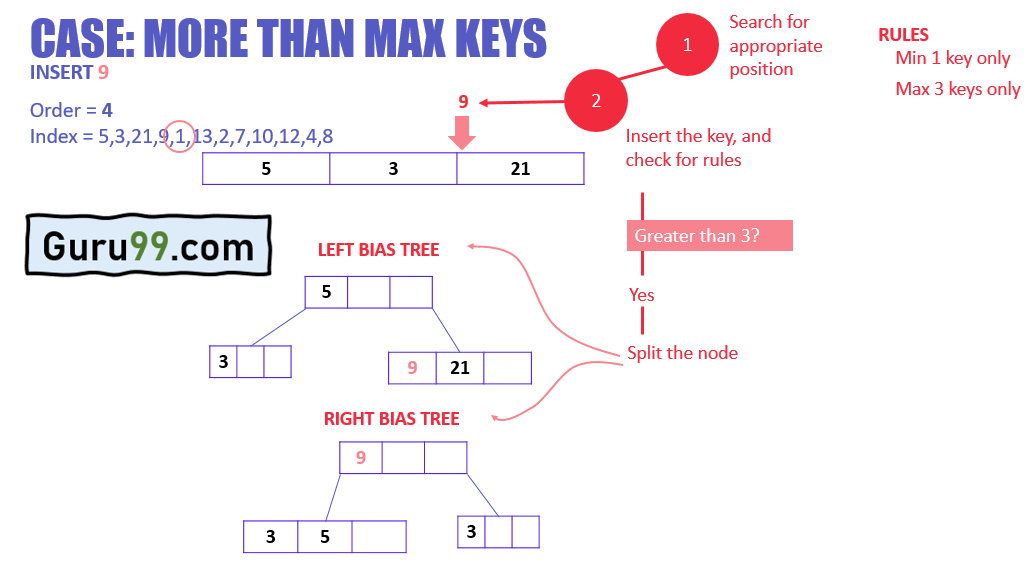
В приведенном выше примере:
- Узел достиг максимального количества ключей
- Узел разделится, и средний ключ станет корневым узлом остальных двух узлов.
- В случае четного количества клавиш средний узел будет выбран смещением влево или вправо.
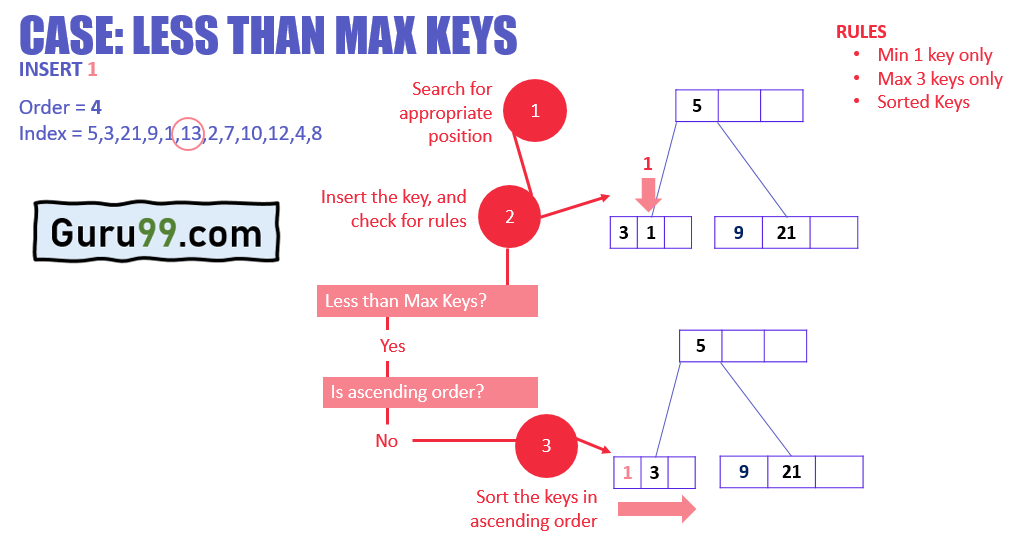
В приведенном выше примере:
- В узле меньше макс ключей
- 1 вставлен рядом с 3, но правило в порядке возрастания нарушено
- Чтобы это исправить, ключи отсортированы
Точно так же 13 и 2 могут быть легко вставлены в узел, так как они удовлетворяют правилу «меньше ключей» для узлов.
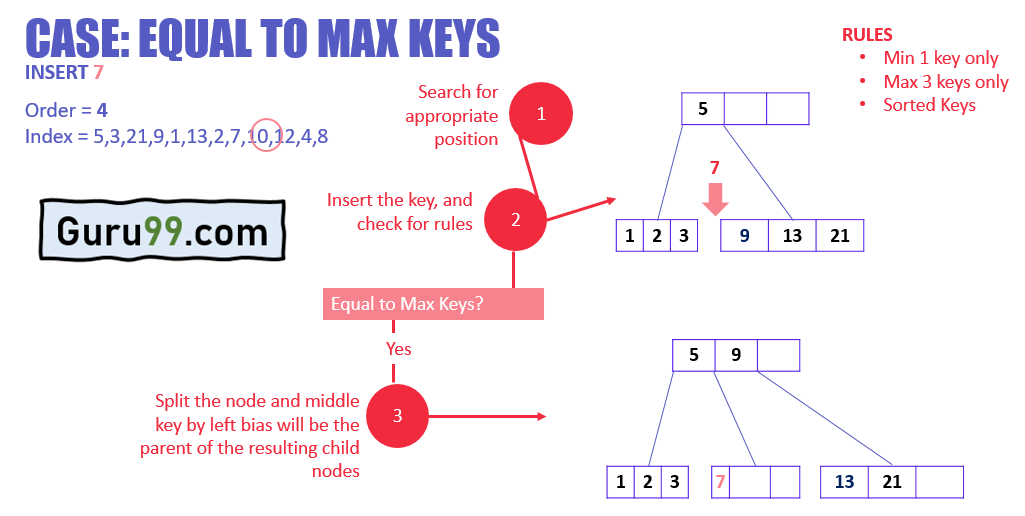
В приведенном выше примере:
- Узел имеет ключи, равные максимальным ключам.
- Ключ вставляется в целевой узел, но он нарушает правило максимальных ключей.
- Целевой узел разделен, и средний ключ по левому смещению теперь является родителем новых дочерних узлов.
- Новые узлы расположены в порядке возрастания.
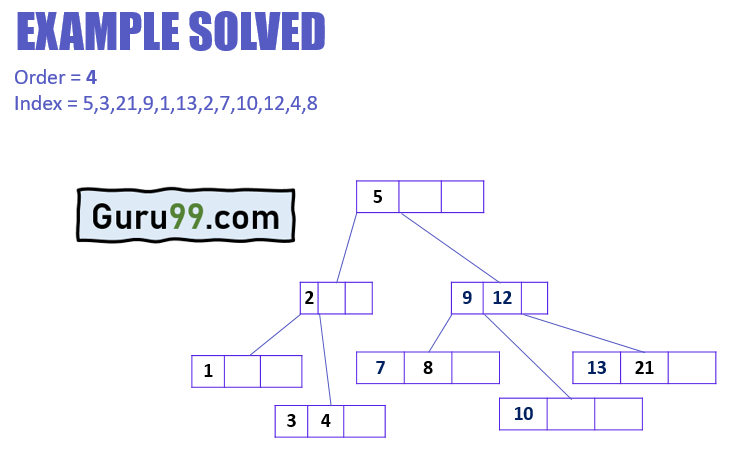
Точно так же, основываясь на вышеуказанных правилах и случаях, остальные значения могут быть легко вставлены в B-дерево.
Удалить операцию
Операция удаления имеет больше правил, чем операции вставки и поиска.
Применяется следующий алгоритм:
- Запустите операцию поиска и найдите целевой ключ в узлах
- Три условия применяются в зависимости от местоположения целевого ключа, как описано в следующих разделах
Если целевой ключ находится в листовом узле
- Цель находится в листовом узле, больше чем мин ключей.
- Удаление этого не будет нарушать свойство B Tree
- Цель находится в листовом узле, она имеет минимальные ключевые узлы
- Удаление этого нарушит свойство B Tree
- Целевой узел может заимствовать ключ от непосредственного левого узла или непосредственного правого узла (одноуровневого)
- Брат или сестра скажут « да», если количество ключей превышает минимальное.
- Ключ будет заимствован из родительского узла, максимальное значение будет передано родительскому узлу, максимальное значение родительского узла будет передано целевому узлу, а целевое значение будет удалено.
- Цель находится в листовом узле, но ни один из братьев и сестер не имеет более минимального количества ключей
- Поиск ключа
- Слияние с братьями и сестрами и минимум родительских узлов
- Всего ключей будет больше минуты
- Целевой ключ будет заменен минимумом родительского узла.
Если целевой ключ находится во внутреннем узле
- Либо выберите предшественник по порядку или преемник по порядку
- В случае предшествующего предшественника будет выбран максимальный ключ из его левого поддерева.
- В случае преемника по порядку будет выбран минимальный ключ из его правого поддерева
- Если предшествующий по порядку целевой ключ имеет больше, чем клавиши min, только тогда он может заменить целевой ключ с максимумом предшествующего по порядку ключа
- Если в предшествующем по порядку целевом ключе не больше, чем min ключей, ищите минимальный ключ в преемнике по порядку.
- Если предшествующий предшественник и преемник целевого ключа имеют ключи меньше чем min, объедините предшественник и преемник.
Если целевой ключ находится в корневом узле
- Заменить максимальным элементом в поддереве предшественника по порядку
- Если после удаления у цели меньше, чем мин ключей, то целевой узел заимствует максимальное значение у своего родного брата через родителя родного брата.
- Максимальное значение родителя будет взято целью, но с узлами максимального значения родного брата.
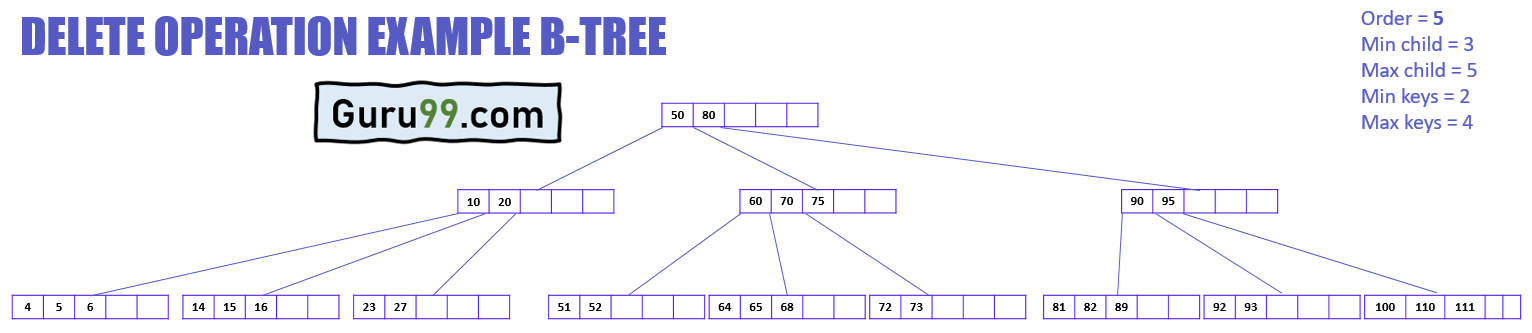
Теперь давайте разберемся с операцией удаления на примере.
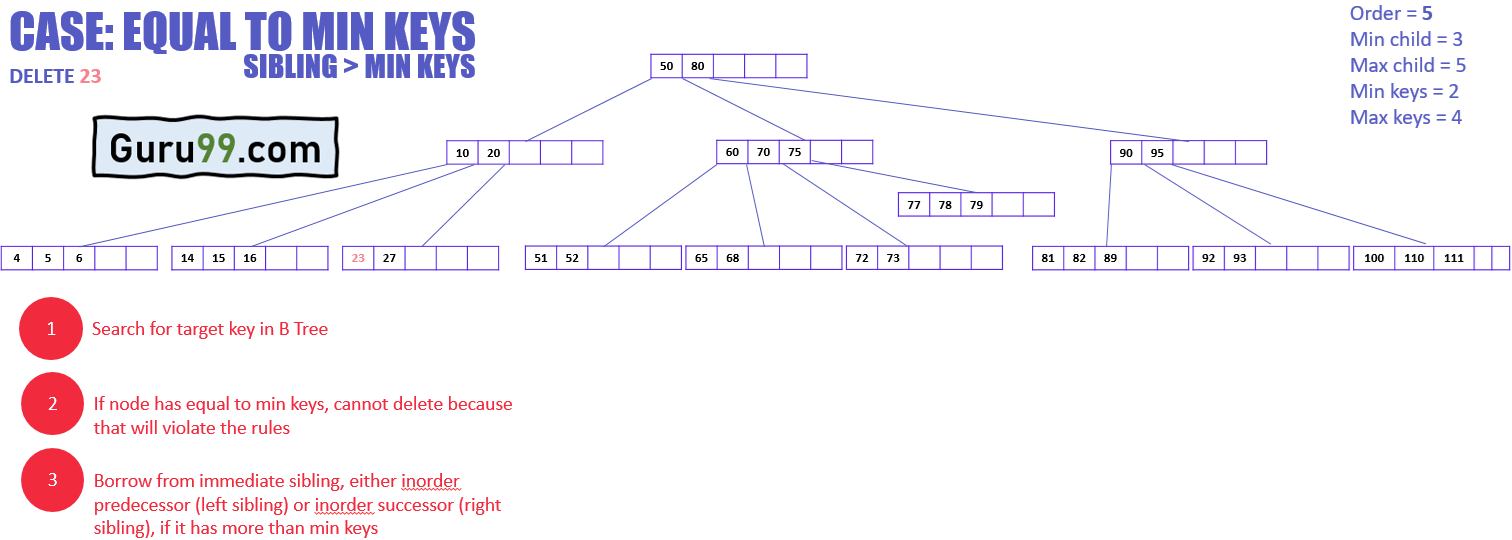
На приведенной выше диаграмме показаны различные случаи операции удаления в B-дереве. Это B-дерево имеет порядок 5, что означает, что минимальное количество дочерних узлов, которое может иметь любой узел, равно 3, а максимальное количество дочерних узлов, которое может иметь любой узел, равно 5. При этом минимальное и максимальное количество ключей любого узла могут иметь 2 и 4 соответственно.
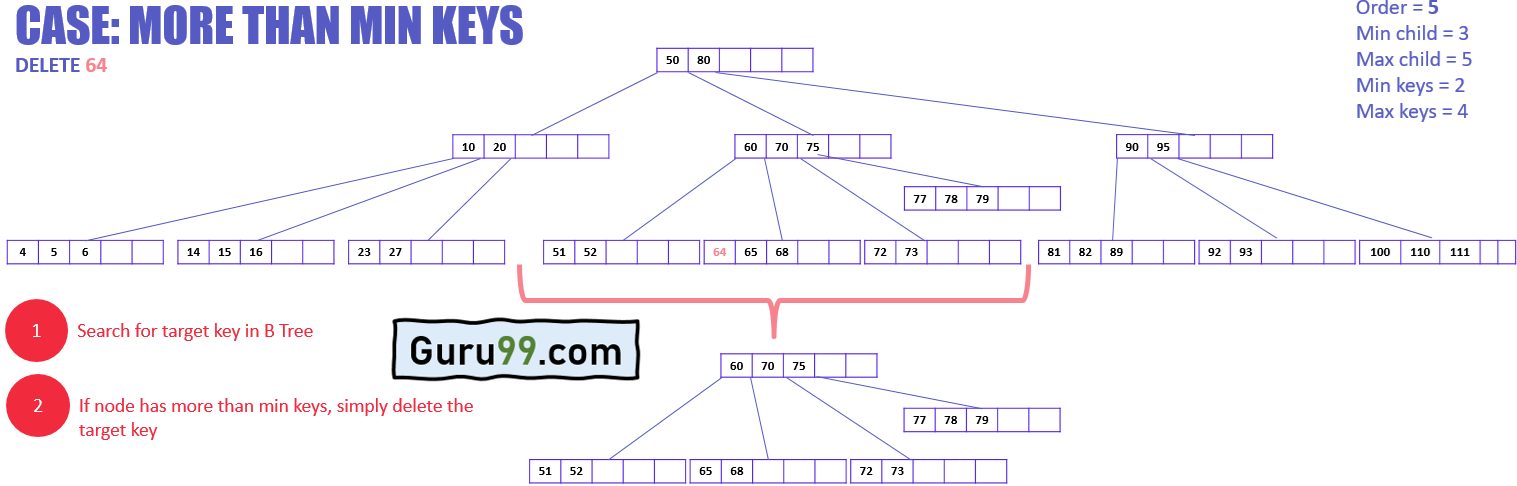
В приведенном выше примере:
- Целевой узел имеет целевой ключ для удаления
- Целевой узел имеет ключи больше чем минимальные ключи
- Просто удалите ключ
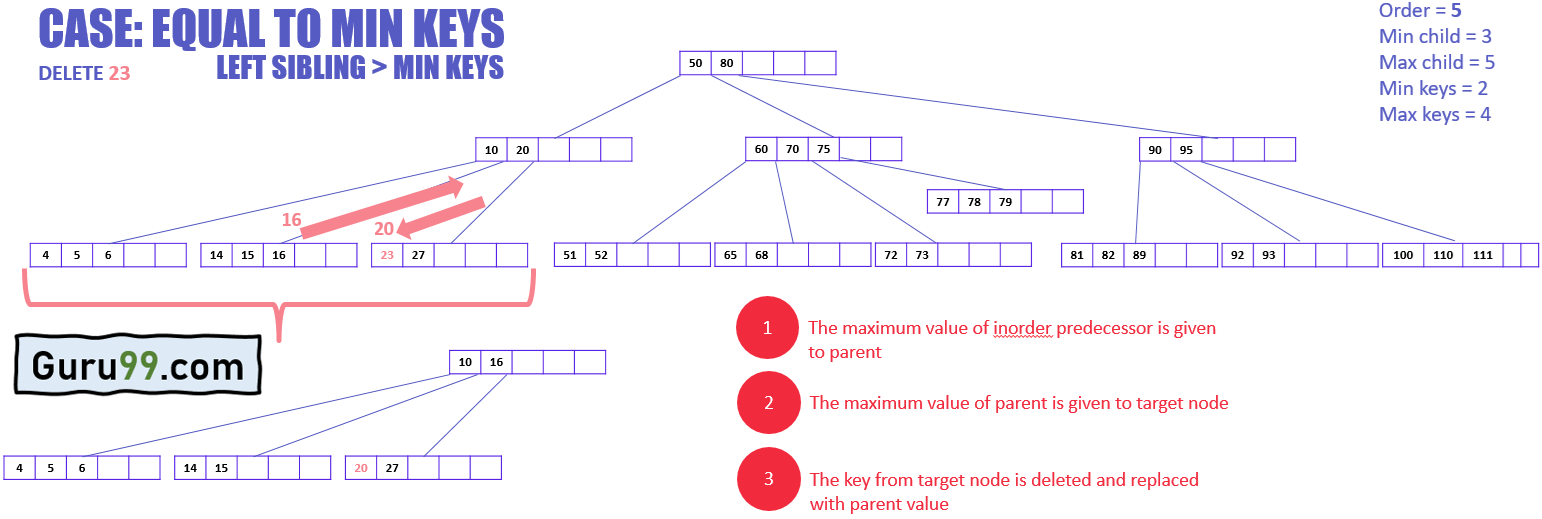
В приведенном выше примере:
- Целевой узел имеет ключи, равные минимальным ключам, поэтому не может удалить его напрямую, так как это нарушит условия
Теперь следующая диаграмма объясняет, как удалить этот ключ:
- Целевой узел заимствует ключ у ближайшего родственника, в данном случае предшественника по порядку (левый брат), потому что у него нет преемника по порядку (правый брат)
- Максимальное значение предшествующего предшественника будет передано родительскому элементу, а родительское максимальное значение будет передано целевому узлу (см. Диаграмму ниже).
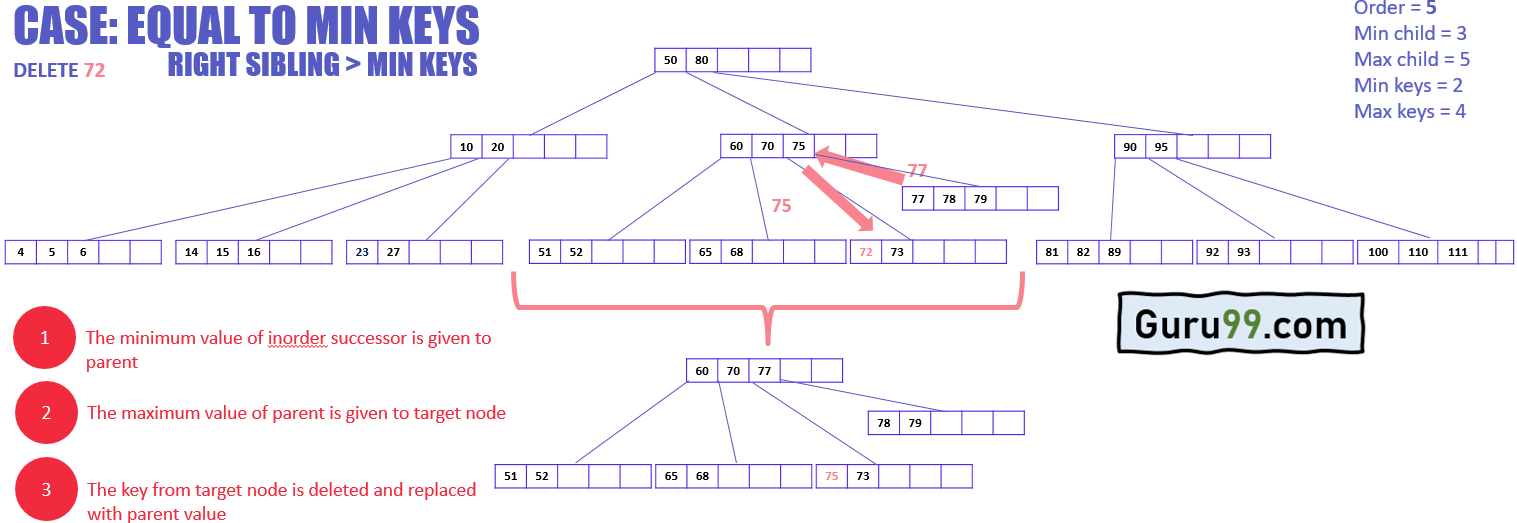
В следующем примере показано, как удалить ключ, которому необходимо значение, из его преемника по порядку.
- Целевой узел заимствует ключ у ближайшего родственника, в данном случае преемника по порядку (правый брат), потому что его предшественник по порядку (левый брат) имеет ключи, равные минимальным ключам.
- Минимальное значение преемника по порядку будет передано родительскому элементу, а родительский элемент передаст максимальное значение целевому узлу.
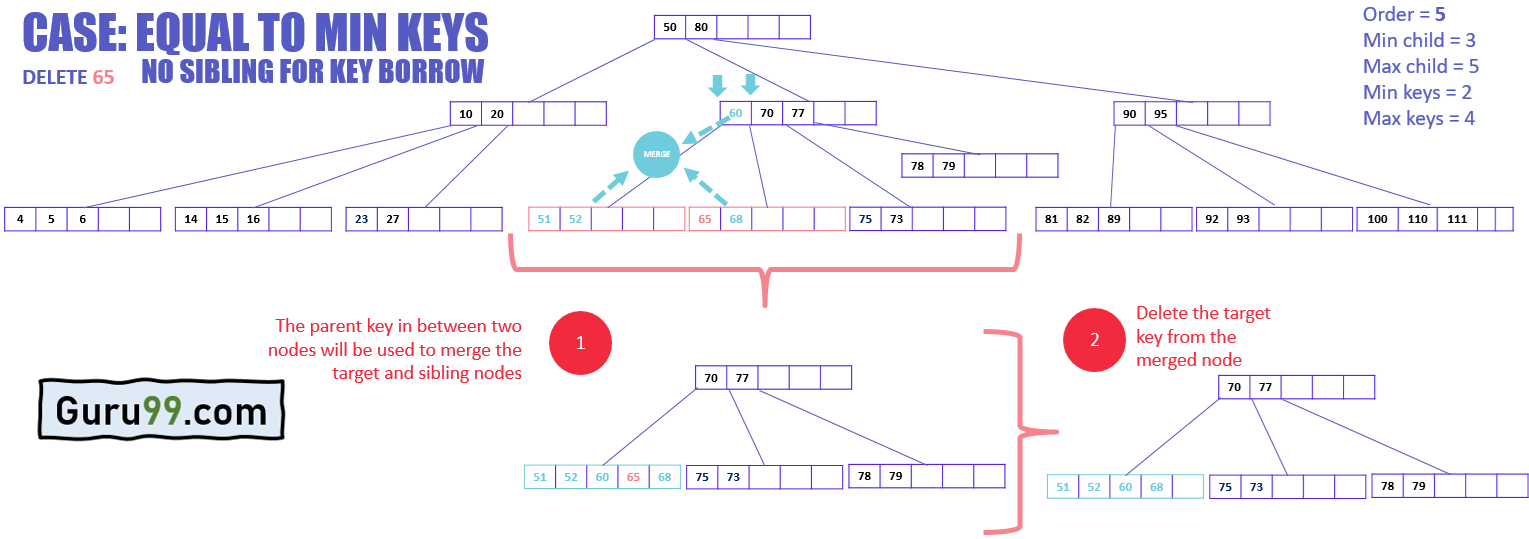
В приведенном ниже примере целевой узел не имеет ни одного родного брата, который мог бы передать свой ключ целевому узлу. Поэтому слияние не требуется.
Смотрите процедуру удаления такого ключа:
- Объединить целевой узел с любым из его ближайших братьев и сестер вместе с родительским ключом
- Выбран ключ из родительского узла, который находится между двумя объединяющимися узлами.
- Удалить целевой ключ из объединенного узла
Удалить псевдокод операции
private int removeBiggestElement()
{
if (root has no child)
remove and return the last element
else {
answer = subset[childCount-1].removeBiggestElement()
if (subset[childCount-1].dataCount < MINIMUM)
fixShort (childCount-1)
return answer
}
}
Выход :
Самый большой элемент удаляется из B-дерева.
Резюме:
- B Tree — это самобалансирующаяся структура данных для лучшего поиска, вставки и удаления данных с диска.
- B Дерево регулируется по степени, указанной
- B Ключи и узлы дерева расположены в порядке возрастания.
- Операция поиска B Tree — самая простая, которая всегда начинается с корня и начинает проверять, больше или меньше целевой ключ, чем значение узла.
- Операция вставки B-дерева довольно детальная, которая сначала находит подходящую позицию вставки для целевого ключа, вставляет ее, оценивает валидность B-дерева в различных случаях, а затем соответствующим образом реструктурирует узлы B-дерева.
- Операция удаления B Tree сначала ищет целевой ключ, который будет удален, удаляет его, оценивает допустимость на основе нескольких случаев, таких как минимальный и максимальный ключи целевого узла, братья и сестры и родительский элемент.