Пометка части речи (PoS)

Маркировка — это разновидность классификации, которая может быть определена как автоматическое присвоение описания токенам. Здесь дескриптор называется тегом, который может представлять одну из частей речи, семантическую информацию и так далее.

Теперь, если мы говорим о тегировании части речи (PoS), то это может быть определено как процесс присвоения одной из частей речи данному слову. Обычно это маркировка POS. Проще говоря, мы можем сказать, что POS-теги — это задача маркировки каждого слова в предложении соответствующей частью речи. Мы уже знаем, что части речи включают в себя существительные, глаголы, наречия, прилагательные, местоимения, союз и их подкатегории.

Большая часть POS-тегов относится к POS-тегам на основе правил, Stochastic POS-тегам и тегам на основе преобразования.

POS-теги на основе правил

Одним из самых старых методов тегирования является POS-тегирование на основе правил. Основанные на правилах тегеры используют словарь или лексику для получения возможных тегов для маркировки каждого слова. Если слово имеет более одного возможного тега, то тегеры на основе правил используют рукописные правила для определения правильного тега. Устранение неоднозначности также может быть выполнено в тегировании на основе правил путем анализа лингвистических особенностей слова наряду с предшествующими, а также последующими словами. Например, предположим, что если предыдущим словом слова является артикль, тогда слово должно быть существительным.

Как следует из названия, вся такая информация в тегах POS на основе правил кодируется в форме правил. Эти правила могут быть:

• Правила контекстного шаблона

• Или, как регулярное выражение, скомпилированное в конечные автоматы, пересекается с лексически неоднозначным представлением предложения.

Правила контекстного шаблона

Или, как регулярное выражение, скомпилированное в конечные автоматы, пересекается с лексически неоднозначным представлением предложения.

Мы также можем понять POS-теги на основе правил по их двухэтапной архитектуре —

• Первый этап — На первом этапе он использует словарь, чтобы назначить каждому слову список потенциальных частей речи.

• Второй этап. На втором этапе используются большие списки рукописных правил устранения неоднозначности, чтобы отсортировать список по одной части речи для каждого слова.

Первый этап — На первом этапе он использует словарь, чтобы назначить каждому слову список потенциальных частей речи.

Второй этап. На втором этапе используются большие списки рукописных правил устранения неоднозначности, чтобы отсортировать список по одной части речи для каждого слова.

Свойства POS-тегов на основе правил

POS-теги на основе правил обладают следующими свойствами:

• Эти тегеры являются тегерами, основанными на знаниях.

• Правила в POS-тегах на основе правил создаются вручную.

• Информация закодирована в виде правил.

• У нас есть ограниченное количество правил примерно около 1000.

• Сглаживание и языковое моделирование явно определены в основанных на правилах тегах.

Эти тегеры являются тегерами, основанными на знаниях.

Правила в POS-тегах на основе правил создаются вручную.

Информация закодирована в виде правил.

У нас есть ограниченное количество правил примерно около 1000.

Сглаживание и языковое моделирование явно определены в основанных на правилах тегах.

Стохастическая POS-маркировка

Другая техника тегирования — это Stochastic POS Tagging. Теперь возникает вопрос: какая модель может быть стохастической? Модель, которая включает в себя частоту или вероятность (статистику), можно назвать стохастической. Любое количество различных подходов к проблеме тегирования части речи можно назвать стохастическим тегером.

Простейший стохастический тегер применяет следующие методы для маркировки POS —

Частотный подход

В этом подходе стохастические тегеры устраняют неоднозначность слов на основе вероятности того, что слово встречается с определенным тегом. Можно также сказать, что тег, встречающийся наиболее часто со словом в обучающем наборе, является тегом, назначенным для неоднозначного экземпляра этого слова. Основная проблема этого подхода заключается в том, что он может привести к недопустимой последовательности тегов.

Вероятности последовательности тегов

Это еще один подход стохастического тегирования, где тегер вычисляет вероятность появления данной последовательности тегов. Это также называется n-граммовый подход. Это называется так, потому что лучший тег для данного слова определяется вероятностью, с которой оно встречается с n предыдущими тегами.

Свойства стохастической POST-метки

Стохастические POS-тегеры обладают следующими свойствами —

• Эта маркировка POS основана на вероятности появления метки.

• Требуется учебный корпус

• Не было бы никакой вероятности для слов, которые не существуют в корпусе.

• Он использует другой корпус тестирования (кроме тренировочного корпуса).

• Это самая простая маркировка POS, потому что она выбирает наиболее частые теги, связанные со словом в учебном корпусе.

Эта маркировка POS основана на вероятности появления метки.

Требуется учебный корпус

Не было бы никакой вероятности для слов, которые не существуют в корпусе.

Он использует другой корпус тестирования (кроме тренировочного корпуса).

Это самая простая маркировка POS, потому что она выбирает наиболее частые теги, связанные со словом в учебном корпусе.

Пометка на основе преобразования

Маркировка на основе преобразования также называется маркировкой Брилла. Это пример обучения на основе преобразования (TBL), который представляет собой алгоритм на основе правил для автоматической маркировки POS для данного текста. TBL, позволяет нам иметь лингвистические знания в удобочитаемой форме, преобразовывает одно состояние в другое с помощью правил преобразования.

Он черпает вдохновение как в предыдущих объясненных тегерах — на основе правил и стохастиков. Если мы видим сходство между тегом на основе правил и преобразованием, то, как и на основе правил, оно также основано на правилах, которые указывают, какие теги нужно назначать каким словам. С другой стороны, если мы видим сходство между стохастиком и тэгером преобразования, то, подобно стохастику, это техника машинного обучения, в которой правила автоматически выводятся из данных.

Работа трансформационного обучения (TBL)

Чтобы понять работу и концепцию основанных на преобразовании тегеров, нам необходимо понять работу обучения, основанного на преобразованиях. Рассмотрим следующие шаги, чтобы понять работу TBL —

• Начните с решения — TBL обычно начинается с некоторого решения проблемы и работает циклично.

• Выбрана наиболее выгодная трансформация — в каждом цикле TBL будет выбирать наиболее выгодную трансформацию.

• Применить к проблеме — преобразование, выбранное на последнем шаге, будет применено к проблеме.

Начните с решения — TBL обычно начинается с некоторого решения проблемы и работает циклично.

Выбрана наиболее выгодная трансформация — в каждом цикле TBL будет выбирать наиболее выгодную трансформацию.

Применить к проблеме — преобразование, выбранное на последнем шаге, будет применено к проблеме.

Алгоритм остановится, когда выбранное преобразование на шаге 2 не добавит больше значения или если больше нет преобразований для выбора. Такое обучение лучше всего подходит для задач классификации.

Преимущества трансформационного обучения (TBL)

Преимущества TBL заключаются в следующем —

• Мы изучаем небольшой набор простых правил, и этих правил достаточно для тегирования.

• Разработка и отладка очень просты в TBL, потому что изученные правила легко понять.

• Сложность в тегировании снижается, потому что в TBL происходит переплетение машинно-обученных и созданных человеком правил.

• Основанный на преобразовании тегер намного быстрее, чем маркер модели Маркова.

Мы изучаем небольшой набор простых правил, и этих правил достаточно для тегирования.

Разработка и отладка очень просты в TBL, потому что изученные правила легко понять.

Сложность в тегировании снижается, потому что в TBL происходит переплетение машинно-обученных и созданных человеком правил.

Основанный на преобразовании тегер намного быстрее, чем маркер модели Маркова.

Недостатки трансформационного обучения (TBL)

Недостатки TBL заключаются в следующем —

• Трансформационное обучение (TBL) не обеспечивает вероятности тегов.

• В TBL время обучения очень большое, особенно на больших корпусах.

Трансформационное обучение (TBL) не обеспечивает вероятности тегов.

В TBL время обучения очень большое, особенно на больших корпусах.

Маркировка POS скрытой марковской модели (HMM)

Прежде чем углубляться в POS-теги HMM, мы должны понять концепцию скрытой модели Маркова (HMM).

Скрытая Марковская Модель

Модель HMM может быть определена как стохастическая модель с двумя вложениями, в которой скрытый стохастический процесс скрыт. Этот скрытый случайный процесс может наблюдаться только через другой набор случайных процессов, который производит последовательность наблюдений.

пример

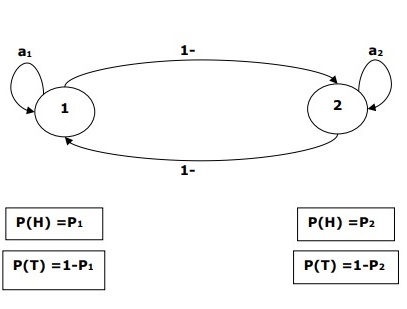
Например, выполняется последовательность экспериментов с подбрасыванием скрытых монет, и мы видим только последовательность наблюдений, состоящую из голов и хвостов. Фактические детали процесса — сколько использованных монет, порядок их выбора — скрыты от нас. Наблюдая эту последовательность голов и хвостов, мы можем построить несколько HMM, чтобы объяснить последовательность. Ниже приводится одна из форм скрытой модели Маркова для этой задачи.

Мы предположили, что в НММ есть два состояния, и каждое из этих состояний соответствует выбору смещенной монеты. Следующая матрица дает вероятности перехода состояния —

$$A = \ begin {bmatrix} a11 & a12 \\ a21 & a22 \ end {bmatrix}$$

Вот,

• a _ij = вероятность перехода из одного состояния в другое из i в j.

• a ₁₁ + a ₁₂ = 1 и a ₂₁ + a ₂₂ = 1

• P ₁ = вероятность глав первой монеты, то есть смещение первой монеты.

• P ₂ = вероятность головы второй монеты, то есть смещение второй монеты.

a _ij = вероятность перехода из одного состояния в другое из i в j.

a ₁₁ + a ₁₂ = 1 и a ₂₁ + a ₂₂ = 1

P ₁ = вероятность глав первой монеты, то есть смещение первой монеты.

P ₂ = вероятность головы второй монеты, то есть смещение второй монеты.

Мы также можем создать модель HMM, предполагая, что есть 3 монеты или больше.

Таким образом, мы можем охарактеризовать HMM следующими элементами:

• N — количество состояний в модели (в приведенном выше примере N = 2, только два состояния).

• M — количество различных наблюдений, которые могут появиться с каждым состоянием в приведенном выше примере (M = 2, т. Е. H или T).

• А, распределение вероятностей перехода состояний — матрица А в приведенном выше примере.

• P — распределение вероятностей наблюдаемых символов в каждом состоянии (в нашем примере P1 и P2).

• Я, начальное состояние распределения.

N — количество состояний в модели (в приведенном выше примере N = 2, только два состояния).

M — количество различных наблюдений, которые могут появиться с каждым состоянием в приведенном выше примере (M = 2, т. Е. H или T).

А, распределение вероятностей перехода состояний — матрица А в приведенном выше примере.

P — распределение вероятностей наблюдаемых символов в каждом состоянии (в нашем примере P1 и P2).

Я, начальное состояние распределения.

Использование HMM для POS-тегов

Процесс маркировки POS — это процесс поиска последовательности тегов, которая, скорее всего, сгенерировала данную последовательность слов. Мы можем смоделировать этот процесс POS, используя скрытую марковскую модель (HMM), где теги — это скрытые состояния, которые дали видимый результат, то есть слова .

Математически, в POS-тегах мы всегда заинтересованы в поиске последовательности тегов (C), которая максимизирует —

P (C | W)

Куда,

C = C ₁ , C ₂ , C ₃ … C _T

W = W ₁ , W ₂ , W ₃ , W _T

С другой стороны, дело в том, что нам нужно много статистических данных для разумной оценки таких последовательностей. Однако, чтобы упростить задачу, мы можем применить некоторые математические преобразования вместе с некоторыми допущениями.

Использование HMM для маркировки POS является частным случаем байесовской помехи. Следовательно, мы начнем с повторения проблемы, используя правило Байеса, которое гласит, что вышеупомянутая условная вероятность равна —

(PROB (C ₁ , …, CT) * PROB (W ₁ , …, WT | C ₁ , …, CT)) / PROB (W ₁ , …, WT)

Мы можем исключить знаменатель во всех этих случаях, потому что нам интересно найти последовательность C, которая максимизирует указанное выше значение. Это не повлияет на наш ответ. Теперь наша проблема сводится к нахождению последовательности C, которая максимизирует —

PROB (C ₁ , …, CT) * PROB (W ₁ , …, WT | C ₁ , …, CT) (1)

Даже после уменьшения проблемы в вышеприведенном выражении потребуется большой объем данных. Мы можем сделать разумные предположения о независимости двух вероятностей в вышеприведенном выражении, чтобы преодолеть проблему.

Первое предположение

Вероятность тега зависит от предыдущего (модель биграммы) или предыдущих двух (модель триграммы) или предыдущих n тегов (модель n-граммы), что математически можно объяснить следующим образом:

PROB (C ₁ , …, C _T ) = Π _{i = 1..T} PROB (C _i | C _{i-n + 1} … C _i-1 ) (n-граммовая модель)

PROB (C ₁ , …, CT) = Π _{i = 1..T} PROB (C _i | C _i-1 ) (биграмная модель)

Начало предложения можно объяснить, приняв начальную вероятность для каждого тега.

PROB (C ₁ | C ₀ ) = _{инициализация} PROB (C ₁ )

Второе предположение

Вторая вероятность в приведенном выше уравнении (1) может быть аппроксимирована, если предположить, что слово появляется в категории, не зависящей от слов в предыдущих или последующих категориях, что можно математически объяснить следующим образом:

PROB (W ₁ , …, W _T | C ₁ , …, C _T ) = Π _{i = 1..T} PROB (W _i | C _i )

Теперь, исходя из двух вышеупомянутых предположений, наша цель сводится к поиску последовательности C, которая максимизирует

Π _{i = 1 … T} PROB (C _i | C _i-1 ) * PROB (W _i | C _i )

Теперь возникает вопрос: действительно ли нам помогло преобразование проблемы в вышеуказанную форму? Ответ — да, это так. Если у нас большой помеченный корпус, то две вероятности в приведенной выше формуле можно рассчитать как —

PROB (C _{i = VERB} | C _{i-1 = NOUN} ) = (количество случаев, когда глагол следует за существительным) / (количество случаев, когда появляется существительное) (2)

PROB (W _i | C _i ) = (количество случаев, когда W _i появляется в C _i ) / (количество случаев, когда C _i появляется) (3)