В этой главе мы разберемся с анализом мирового уровня в обработке естественного языка.
Регулярные выражения
Регулярное выражение (RE) — это язык для указания строк текстового поиска. RE помогает нам сопоставлять или находить другие строки или наборы строк, используя специальный синтаксис, содержащийся в шаблоне. Регулярные выражения используются для поиска текстов в UNIX, а также в MS WORD одинаковым способом. У нас есть различные поисковые системы, использующие ряд функций RE.
Свойства регулярных выражений
Ниже приведены некоторые важные свойства RE —
-
Американский математик Стивен Коул Клин формализовал язык регулярных выражений.
-
RE — это формула на специальном языке, которую можно использовать для указания простых классов строк, последовательности символов. Другими словами, мы можем сказать, что RE является алгебраической нотацией для характеристики набора строк.
-
Регулярное выражение требует двух вещей: одна — это шаблон, который мы хотим искать, а другая — это совокупность текста, из которого мы должны искать.
Американский математик Стивен Коул Клин формализовал язык регулярных выражений.
RE — это формула на специальном языке, которую можно использовать для указания простых классов строк, последовательности символов. Другими словами, мы можем сказать, что RE является алгебраической нотацией для характеристики набора строк.
Регулярное выражение требует двух вещей: одна — это шаблон, который мы хотим искать, а другая — это совокупность текста, из которого мы должны искать.
Математически Регулярное выражение может быть определено следующим образом:
-
ε является регулярным выражением, которое указывает, что язык имеет пустую строку.
-
φ является регулярным выражением, которое обозначает, что это пустой язык.
-
Если X и Y являются регулярными выражениями, то
-
X, Y
-
XY (объединение XY)
-
X + Y (Союз X и Y)
-
X *, Y * (Клин Закрытие X и Y)
-
ε является регулярным выражением, которое указывает, что язык имеет пустую строку.
φ является регулярным выражением, которое обозначает, что это пустой язык.
Если X и Y являются регулярными выражениями, то
X, Y
XY (объединение XY)
X + Y (Союз X и Y)
X *, Y * (Клин Закрытие X и Y)
также регулярные выражения.
-
Если строка получена из вышеуказанных правил, то это также будет регулярное выражение.
Если строка получена из вышеуказанных правил, то это также будет регулярное выражение.
Примеры регулярных выражений
В следующей таблице приведены несколько примеров регулярных выражений:
| Регулярные выражения | Обычный набор |
|---|---|
| (0 + 10 *) | {0, 1, 10, 100, 1000, 10000,…} |
| (0 * 10 *) | {1, 01, 10, 010, 0010,…} |
| (0 + ε) (1 + ε) | {ε, 0, 1, 01} |
| (А + б) * | Это будет набор строк a и b любой длины, который также содержит пустую строку, т. Е. {Ε, a, b, aa, ab, bb, ba, aaa …….} |
| (А + б) * АВВ | Это будет набор строк из a и b, оканчивающихся строкой abb, т.е. {abb, aabb, babb, aaabb, ababb, ………… ..} |
| (11) * | Это будет набор, состоящий из четного числа 1, которое также содержит пустую строку, т. Е. {Ε, 11, 1111, 111111, ……….} |
| (Аа) * (бб) * б | Это будет набор строк, состоящий из четного числа a, за которым следует нечетное количество b, т.е. {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, ………… ..} |
| (aa + ab + ba + bb) * | Это будет строка a и b одинаковой длины, которая может быть получена путем объединения любой комбинации строк aa, ab, ba и bb, включая ноль, т. Е. {Aa, ab, ba, bb, aaab, aaba, …………. .} |
Регулярные множества и их свойства
Он может быть определен как набор, который представляет значение регулярного выражения и состоит из определенных свойств.
Свойства регулярных множеств
-
Если мы сделаем объединение двух регулярных наборов, то результирующий набор также будет регулярным.
-
Если мы сделаем пересечение двух регулярных множеств, то результирующий набор также будет регулярным.
-
Если мы сделаем дополнение регулярных множеств, то результирующий набор также будет регулярным.
-
Если мы сделаем различие двух регулярных наборов, то результирующий набор также будет регулярным.
-
Если мы сделаем обращение регулярных множеств, то результирующий набор также будет регулярным.
-
Если мы возьмем замыкание регулярных множеств, то результирующий набор также будет регулярным.
-
Если мы сделаем объединение двух регулярных наборов, то результирующий набор также будет регулярным.
Если мы сделаем объединение двух регулярных наборов, то результирующий набор также будет регулярным.
Если мы сделаем пересечение двух регулярных множеств, то результирующий набор также будет регулярным.
Если мы сделаем дополнение регулярных множеств, то результирующий набор также будет регулярным.
Если мы сделаем различие двух регулярных наборов, то результирующий набор также будет регулярным.
Если мы сделаем обращение регулярных множеств, то результирующий набор также будет регулярным.
Если мы возьмем замыкание регулярных множеств, то результирующий набор также будет регулярным.
Если мы сделаем объединение двух регулярных наборов, то результирующий набор также будет регулярным.
Конечные Государственные Автоматы
Термин «автоматы», производный от греческого слова «αὐτόματα», означающего «самодействующий», является множественным числом автомата, которое может быть определено как абстрактное самоходное вычислительное устройство, которое автоматически следует заданной последовательности операций.
Автомат с конечным числом состояний называется конечным автоматом (FA) или конечным автоматом (FSA).
Математически автомат может быть представлен 5-кортежем (Q, Σ, δ, q0, F), где —
-
Q — конечное множество состояний.
-
Σ — это конечный набор символов, называемый алфавитом автомата.
-
δ — функция перехода
-
q0 — начальное состояние, из которого обрабатывается любой вход (q0 ∈ Q).
-
F — множество конечных состояний / состояний Q (F ⊆ Q).
Q — конечное множество состояний.
Σ — это конечный набор символов, называемый алфавитом автомата.
δ — функция перехода
q0 — начальное состояние, из которого обрабатывается любой вход (q0 ∈ Q).
F — множество конечных состояний / состояний Q (F ⊆ Q).
Связь между конечными автоматами, регулярными грамматиками и регулярными выражениями
Следующие пункты дадут нам четкое представление о связи между конечными автоматами, регулярными грамматиками и регулярными выражениями —
-
Поскольку мы знаем, что конечные автоматы являются теоретической основой вычислительной работы, а регулярные выражения являются одним из способов их описания.
-
Можно сказать, что любое регулярное выражение может быть реализовано как FSA, а любое FSA может быть описано с помощью регулярного выражения.
-
С другой стороны, регулярное выражение — это способ охарактеризовать разновидность языка, называемого регулярным языком. Следовательно, мы можем сказать, что регулярный язык может быть описан как с помощью FSA, так и регулярного выражения.
-
Регулярная грамматика, формальная грамматика, которая может быть правильной или правильной слева, является еще одним способом характеристики обычного языка.
Поскольку мы знаем, что конечные автоматы являются теоретической основой вычислительной работы, а регулярные выражения являются одним из способов их описания.
Можно сказать, что любое регулярное выражение может быть реализовано как FSA, а любое FSA может быть описано с помощью регулярного выражения.
С другой стороны, регулярное выражение — это способ охарактеризовать разновидность языка, называемого регулярным языком. Следовательно, мы можем сказать, что регулярный язык может быть описан как с помощью FSA, так и регулярного выражения.
Регулярная грамматика, формальная грамматика, которая может быть правильной или правильной слева, является еще одним способом характеристики обычного языка.
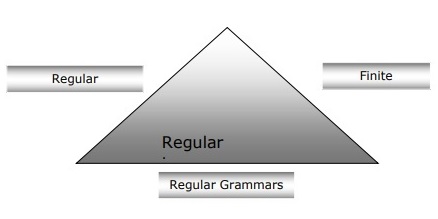
Следующая диаграмма показывает, что конечные автоматы, регулярные выражения и регулярные грамматики являются эквивалентными способами описания регулярных языков.
Типы конечной государственной автоматизации (ФСА)
Автоматизация конечных состояний бывает двух типов. Давайте посмотрим, что это за типы.
Детерминированная конечная автоматизация (DFA)
Это может быть определено как тип конечной автоматизации, в которой для каждого входного символа мы можем определить состояние, в которое машина перейдет. Он имеет конечное число состояний, поэтому машина называется детерминированным конечным автоматом (DFA).
Математически DFA может быть представлен 5-кортежем (Q, Σ, δ, q0, F), где —
-
Q — конечное множество состояний.
-
Σ — это конечный набор символов, называемый алфавитом автомата.
-
δ — функция перехода, где δ: Q × Σ → Q.
-
q0 — начальное состояние, из которого обрабатывается любой вход (q0 ∈ Q).
-
F — множество конечных состояний / состояний Q (F ⊆ Q).
Q — конечное множество состояний.
Σ — это конечный набор символов, называемый алфавитом автомата.
δ — функция перехода, где δ: Q × Σ → Q.
q0 — начальное состояние, из которого обрабатывается любой вход (q0 ∈ Q).
F — множество конечных состояний / состояний Q (F ⊆ Q).
В то время как графически DFA может быть представлен диаграммами, называемыми диаграммами состояний, где —
-
Состояния представлены вершинами .
-
Переходы показаны помеченными дугами .
-
Начальное состояние представлено пустой входящей дугой .
-
Конечное состояние представлено двойным кружком .
Состояния представлены вершинами .
Переходы показаны помеченными дугами .
Начальное состояние представлено пустой входящей дугой .
Конечное состояние представлено двойным кружком .
Пример ДФА
Предположим, что DFA будет
-
Q = {a, b, c},
-
Σ = {0, 1},
-
q 0 = {а},
-
F = {c},
-
Функция перехода δ показана в таблице следующим образом:
Q = {a, b, c},
Σ = {0, 1},
q 0 = {а},
F = {c},
Функция перехода δ показана в таблице следующим образом:
| Текущее состояние | Следующее состояние для ввода 0 | Следующее состояние для ввода 1 |
|---|---|---|
| В | ||
| В | б | |
| С | с | С |
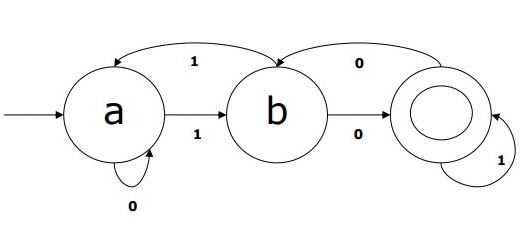
Графическое представление этого DFA будет следующим:
Недетерминированная конечная автоматизация (NDFA)
Это может быть определено как тип конечной автоматизации, где для каждого входного символа мы не можем определить состояние, в которое будет перемещаться машина, т.е. машина может перейти в любую комбинацию состояний. Он имеет конечное число состояний, поэтому машина называется недетерминированной конечной автоматизацией (NDFA).
Математически NDFA может быть представлен 5-кортежем (Q, Σ, δ, q0, F), где —
-
Q — конечное множество состояний.
-
Σ — это конечный набор символов, называемый алфавитом автомата.
-
δ: — функция перехода, где δ: Q × Σ → 2 Q.
-
q0: — начальное состояние, из которого обрабатывается любой вход (q0 ∈ Q).
-
F: -множество конечного состояния / состояний Q (F ⊆ Q).
Q — конечное множество состояний.
Σ — это конечный набор символов, называемый алфавитом автомата.
δ: — функция перехода, где δ: Q × Σ → 2 Q.
q0: — начальное состояние, из которого обрабатывается любой вход (q0 ∈ Q).
F: -множество конечного состояния / состояний Q (F ⊆ Q).
В то время как графически (так же, как DFA), NDFA может быть представлен диаграммами, называемыми диаграммами состояний, где —
-
Состояния представлены вершинами .
-
Переходы показаны помеченными дугами .
-
Начальное состояние представлено пустой входящей дугой .
-
Конечное состояние представлено двойным кружком .
Состояния представлены вершинами .
Переходы показаны помеченными дугами .
Начальное состояние представлено пустой входящей дугой .
Конечное состояние представлено двойным кружком .
Пример NDFA
Предположим, что NDFA будет
-
Q = {a, b, c},
-
Σ = {0, 1},
-
q 0 = {а},
-
F = {c},
-
Функция перехода δ показана в таблице следующим образом:
Q = {a, b, c},
Σ = {0, 1},
q 0 = {а},
F = {c},
Функция перехода δ показана в таблице следующим образом:
| Текущее состояние | Следующее состояние для ввода 0 | Следующее состояние для ввода 1 |
|---|---|---|
| а, б | В | |
| В | С | а, с |
| С | До нашей эры | С |
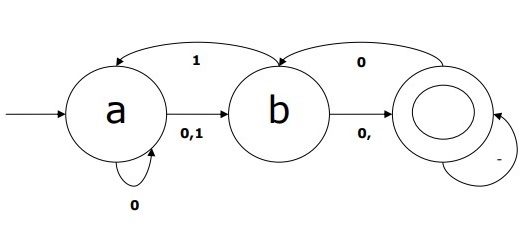
Графическое представление этого NDFA будет следующим:
Морфологический анализ
Термин морфологический анализ связан с анализом морфем. Мы можем определить морфологический анализ как проблему распознавания того, что слово разбивается на более мелкие значимые единицы, называемые морфемами, создавая для него некую лингвистическую структуру. Например, мы можем разбить слово « лисы» на два, « лиса» и « -ес» . Мы видим, что слово « лисы» состоит из двух морфем: одна — лиса, а другая — «да».
В другом смысле мы можем сказать, что морфология — это изучение
-
Формирование слов.
-
Происхождение слов.
-
Грамматические формы слов.
-
Использование префиксов и суффиксов в образовании слов.
-
Как формируются части речи (PoS) языка.
Формирование слов.
Происхождение слов.
Грамматические формы слов.
Использование префиксов и суффиксов в образовании слов.
Как формируются части речи (PoS) языка.
Типы морфем
Морфемы, наименьшие смыслосодержащие единицы, можно разделить на два типа:
-
Стебли
-
Порядок слов
Стебли
Порядок слов
Стебли
Это основная смысловая единица слова. Можно также сказать, что это корень слова. Например, в слове лисы ствол — лиса.
-
Аффиксы. Как следует из названия, они добавляют словам дополнительный смысл и грамматические функции. Например, в слове «лисы» аффикс — ес.
Аффиксы. Как следует из названия, они добавляют словам дополнительный смысл и грамматические функции. Например, в слове «лисы» аффикс — ес.
Кроме того, аффиксы также можно разделить на следующие четыре типа:
-
Префиксы. Как следует из названия, префиксы предшествуют основам. Например, в слове unbuckle un является префиксом.
-
Суффиксы — Как следует из названия, суффиксы следуют за основанием. Например, в слове кошки суффикс -s.
-
Инфиксы — Как следует из названия, инфиксы вставляются в ствол. Например, слово cupful можно использовать для множественного числа как cupsful, используя -s в качестве инфикса.
-
Circumfixes — они предшествуют и следуют за стеблем. Примеров обрезаний на английском языке очень мало. Очень распространенный пример — «A-ing», где мы можем использовать -A перед, а -ing после ствола.
Префиксы. Как следует из названия, префиксы предшествуют основам. Например, в слове unbuckle un является префиксом.
Суффиксы — Как следует из названия, суффиксы следуют за основанием. Например, в слове кошки суффикс -s.
Инфиксы — Как следует из названия, инфиксы вставляются в ствол. Например, слово cupful можно использовать для множественного числа как cupsful, используя -s в качестве инфикса.
Circumfixes — они предшествуют и следуют за стеблем. Примеров обрезаний на английском языке очень мало. Очень распространенный пример — «A-ing», где мы можем использовать -A перед, а -ing после ствола.
Порядок слов
Порядок слов будет определяться путем морфологического анализа. Давайте теперь посмотрим требования для построения морфологического парсера —
Словарный запас
Самым первым требованием для построения морфологического синтаксического анализатора является лексикон, который включает в себя список основ и аффиксов вместе с основной информацией о них. Например, информация о том, является ли ствол существительным или глагольным стволом и т. Д.
Morphotactics
В основном это модель упорядочения морфем. В другом смысле модель, объясняющая, какие классы морфем могут следовать за другими классами морфем внутри слова. Например, морфотаксический факт заключается в том, что морфема английского множественного числа всегда следует за существительным, а не предшествует ему.
Орфографические правила
Эти правила правописания используются для моделирования изменений, происходящих в слове. Например, правило преобразования у в слова, например, город + с = города, а не города.