Здесь мы обсудим другие методы классификации, такие как генетические алгоритмы, подход грубых множеств и подход нечетких множеств.
Генетические алгоритмы
Идея генетического алгоритма вытекает из естественной эволюции. В генетическом алгоритме, прежде всего, создается начальная популяция. Эта начальная популяция состоит из случайно сгенерированных правил. Мы можем представить каждое правило строкой битов.
Например, в данном обучающем наборе выборки описываются двумя логическими атрибутами, такими как A1 и A2. И этот данный обучающий набор содержит два класса, таких как C1 и C2.
Мы можем закодировать правило ЕСЛИ А1, а не А2, а затем С2 в битовую строку 100 . В этом битовом представлении два крайних левых бита представляют атрибуты А1 и А2 соответственно.
Аналогично, правило ЕСЛИ НЕ А1 И НЕ А2, ТО С1 может быть закодировано как 001 .
Примечание. Если атрибут имеет значения K, где K> 2, то мы можем использовать биты K для кодирования значений атрибута. Классы также кодируются таким же образом.
Нужно помнить
-
Основываясь на понятии выживания наиболее приспособленных, формируется новая популяция, которая состоит из наиболее приспособленных правил в текущей популяции и значений этих правил для потомства.
-
Пригодность правила оценивается по точности его классификации на наборе обучающих выборок.
-
Генетические операторы, такие как скрещивание и мутация, применяются для создания потомства.
-
В кроссовере подстрока из пары правил меняются местами, образуя новую пару правил.
-
При мутации случайно выбранные биты в строке правила инвертируются.
Основываясь на понятии выживания наиболее приспособленных, формируется новая популяция, которая состоит из наиболее приспособленных правил в текущей популяции и значений этих правил для потомства.
Пригодность правила оценивается по точности его классификации на наборе обучающих выборок.
Генетические операторы, такие как скрещивание и мутация, применяются для создания потомства.
В кроссовере подстрока из пары правил меняются местами, образуя новую пару правил.
При мутации случайно выбранные биты в строке правила инвертируются.
Грубый подход
Мы можем использовать приблизительный подход, чтобы обнаружить структурные отношения в неточных и шумных данных.
Примечание. Этот подход может применяться только к дискретным атрибутам. Следовательно, непрерывнозначные атрибуты должны быть дискретизированы перед его использованием.
Rough Set Theory основана на установлении классов эквивалентности в данных данных обучения. Кортежи, образующие класс эквивалентности, неразличимы. Это означает, что образцы идентичны в отношении атрибутов, описывающих данные.
В данных реального мира есть несколько классов, которые нельзя различить с точки зрения доступных атрибутов. Мы можем использовать грубые наборы, чтобы приблизительно определить такие классы.
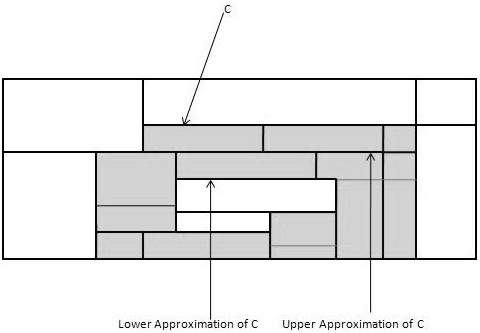
Для данного класса C грубое определение набора аппроксимируется двумя наборами следующим образом:
-
Нижняя аппроксимация C — нижняя аппроксимация C состоит из всех кортежей данных, которые, основываясь на знании атрибута, наверняка принадлежат классу C.
-
Верхняя аппроксимация C — верхняя аппроксимация C состоит из всех кортежей, которые, основываясь на знании атрибутов, не могут быть описаны как не принадлежащие C.
Нижняя аппроксимация C — нижняя аппроксимация C состоит из всех кортежей данных, которые, основываясь на знании атрибута, наверняка принадлежат классу C.
Верхняя аппроксимация C — верхняя аппроксимация C состоит из всех кортежей, которые, основываясь на знании атрибутов, не могут быть описаны как не принадлежащие C.
На следующей диаграмме показана верхняя и нижняя аппроксимация класса C —
Подходы нечетких множеств
Теория нечетких множеств также называется теорией вероятностей. Эта теория была предложена Лотфи Заде в 1965 году как альтернатива двухзначной логике и теории вероятностей . Эта теория позволяет нам работать на высоком уровне абстракции. Это также дает нам средства для неточного измерения данных.
Теория нечетких множеств также позволяет нам иметь дело с неопределенными или неточными фактами. Например, членство в группе с высокими доходами является точным (например, если 50 000 долларов высоки, то примерно 49 000 и 48 000 долларов США). В отличие от традиционного набора CRISP, где элемент либо принадлежит S, либо его дополнению, но в теории нечетких множеств элемент может принадлежать более чем одному нечеткому множеству.
Например, значение дохода в 49 000 долларов относится как к средним, так и к высоким нечетким множествам, но в разной степени. Нечеткое обозначение набора для этого значения дохода выглядит следующим образом:
m medium_income ($49k)=0.15 and m high_income ($49k)=0.96
где «m» — функция принадлежности, которая работает с нечеткими множествами medium_income и high_income соответственно. Эта запись может быть схематически показана следующим образом: