В этом подходе одно булево выражение минимизируется в эквивалентное выражение путем применения булевых тождеств.
Проблема 1
Минимизируйте следующее логическое выражение, используя логические тождества —
F(A,B,C)=A′B+BC′+BC+AB′C′
Решение
Учитывая, F(A,B,C)=A′B+BC′+BC+AB′C′
Или F(A,B,C)=A′B+(BC′+BC′)+BC+AB′C′
[По идемпотентному закону, BC ‘= BC’ + BC ‘]
Или F(A,B,C)=A′B+(BC′+BC)+(BC′+AB′C′)
Или F(A,B,C)=A′B+B(C′+C)+C′(B+AB′)
[По распределительным законам]
Или F(A,B,C)=A′B+B.1+C′(B+A)
[(C ‘+ C) = 1 и закон поглощения (B + AB’) = (B + A)]
Или F(A,B,C)=A′B+B+C′(B+A)
[B.1 = B]
Или F(A,B,C)=B(A′+1)+C′(B+A)
Или F(A,B,C)=B.1+C′(B+A)
[(A ‘+ 1) = 1]
Или F(A,B,C)=B+C′(B+A)
[As, B.1 = B]
Или F(A,B,C)=B+BC′+AC′
Или F(A,B,C)=B(1+C′)+AC′
Или F(A,B,C)=B.1+AC′
[As, (1 + C ‘) = 1]
Или F(A,B,C)=B+AC′
[As, B.1 = B]
Итак, F(A,B,C)=B+AC′ является минимизированной формой.
Проблема 2
Минимизируйте следующее логическое выражение, используя логические тождества —
F(A,B,C)=(A+B)(A+C)
Решение
Учитывая, F(A,B,C)=(A+B)(A+C)
Или F(A,B,C)=AA+AC+BA+BC [Применение дистрибутивного правила]
Или F(A,B,C)=A+AC+BA+BC [Применение закона Идемпотента]
Или F(A,B,C)=A(1+C)+BA+BC [Применение закона распределения]
Или F(A,B,C)=A+BA+BC [Применение закона доминирования]
Или F(A,B,C)=(A+1).A+BC [Применение закона распределения]
Или F(A,B,C)=1.A+BC [Применение закона доминирования]
Или F(A,B,C)=A+BC [Применение закона доминирования]
Итак, F(A,B,C)=A+BC — это минимизированная форма.
Карно Карты
Карта Карно (K – map), представленная Морисом Карнофином в 1953 году, представляет собой сетчатое представление таблицы истинности, которая используется для упрощения выражений булевой алгебры. Карта Карно имеет ноль и одну запись в разных позициях. Он обеспечивает группировку логических выражений с общими факторами и исключает нежелательные переменные из выражения. На K-карте пересечение вертикальной или горизонтальной границы ячейки всегда является изменением только одной переменной.
Пример 1
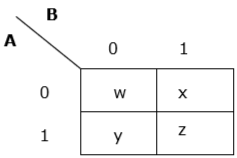
Произвольная таблица истинности взята ниже —
| В | Операция Б | |
|---|---|---|
| 0 | 0 | вес |
| 0 | 1 | Икс |
| 1 | 0 | Y |
| 1 | 1 | Z |
Теперь мы сделаем k-карту для приведенной выше таблицы истинности —
Пример 2
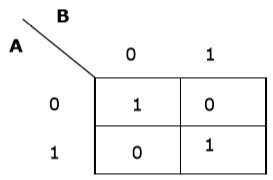
Теперь мы сделаем K-карту для выражения — AB + A’B ‘
Упрощение с использованием K-карты
K-map использует некоторые правила для упрощения логических выражений, объединяя смежные ячейки в один термин. Правила описаны ниже —
Правило 1 — Любая ячейка, содержащая ноль, не может быть сгруппирована.
Неправильная группировка
Правило 2 — Группы должны содержать 2n ячеек (n, начиная с 1).
Неправильная группировка
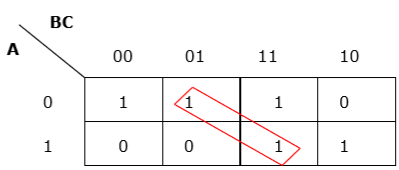
Правило 3 — Группировка должна быть горизонтальной или вертикальной, но не должна быть диагональной.
Неправильная диагональная группировка
Правильная вертикальная группировка
Правильная горизонтальная группировка
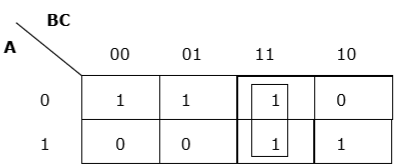
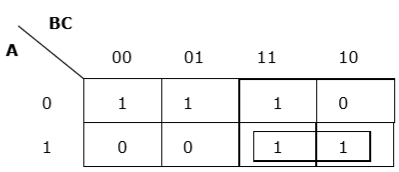
Правило 4 — Группы должны быть охвачены как можно шире.
Недостаточная группировка
Правильная группировка
Правило 5 — Если 1 из любой ячейки не может быть сгруппирована с какой-либо другой ячейкой, она будет действовать как сама группа.
Правильная группировка
Правило 6 — Группы могут перекрываться, но должно быть как можно меньше групп.
Правильная группировка
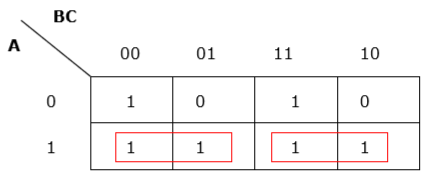
Правило 7 — Самая левая ячейка / ячейки могут быть сгруппированы с самой правой ячейкой / ячейками, а самая верхняя ячейка / ячейки может быть сгруппирована с самой нижней ячейкой / ячейками.
Правильная группировка
проблема
Минимизируйте следующее логическое выражение, используя K-map —
F(A,B,C)=A′BC+A′BC′+AB′C′+AB′C
Решение
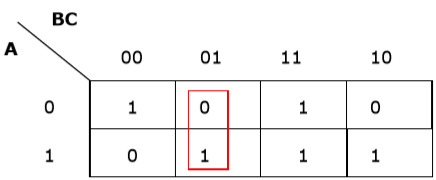
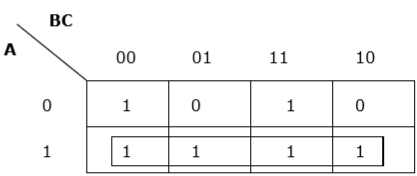
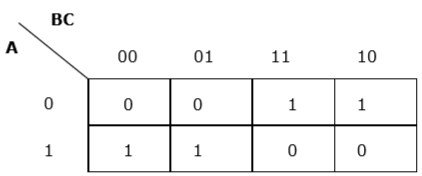
Каждый термин помещается в k-карту, и мы получаем следующее —
K-карта для F (A, B, C)
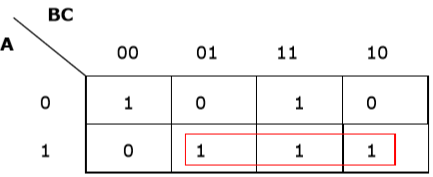
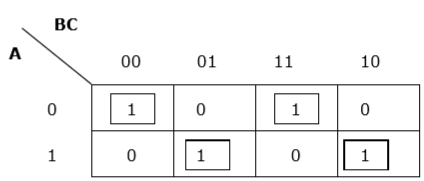
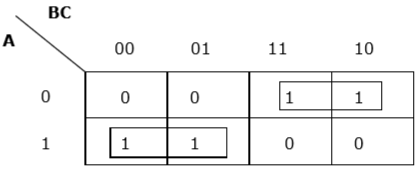
Теперь мы сгруппируем ячейки 1 согласно правилам, изложенным выше —
K-карта для F (A, B, C)
У нас есть две группы, которые называются A′B и AB′. Следовательно, F(A,B,C)=A′B+AB′=A oplusB. Это минимизированная форма.