Граф и графические модели

В предыдущей части были представлены различные инструменты для рассуждения, проверки и решения проблем. В этой части мы рассмотрим дискретные структуры, которые составляют основу постановки многих реальных проблем.

Мы рассмотрим две дискретные структуры: графы и деревья. Граф — это набор точек, называемых узлами или вершинами, которые связаны набором линий, называемых ребрами. Изучение графов, или теория графов, является важной частью ряда дисциплин в области математики, инженерии и информатики.

Что такое график?

Определение — граф (обозначается как $G = (V, E)$ ) состоит из непустого набора вершин или узлов V и множества ребер E.

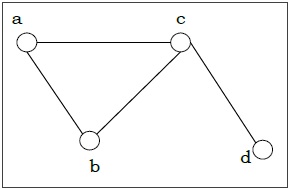
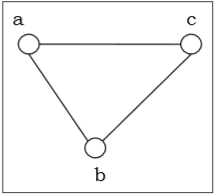
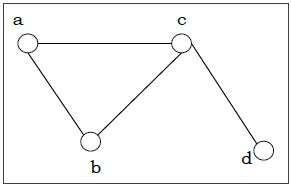
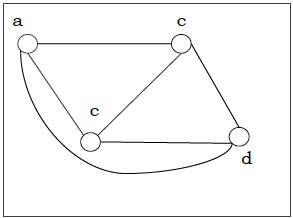
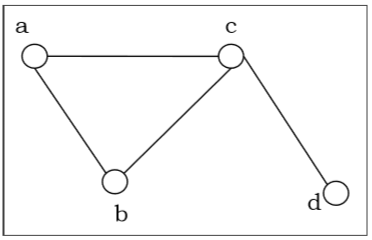
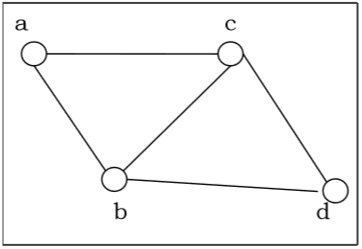
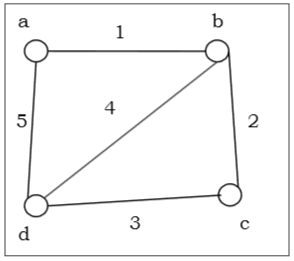
Пример. Рассмотрим граф: $G = (V, E)$ , где $V = \ lbrace a, b, c, d \ rbrace$ и $E = \ lbrace \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace b, c \ rbrace, \ lbrace c, d \ rbrace \ rbrace$

Степень вершины . Степень вершины V графа G (обозначается через deg (V)) — это число ребер, инцидентных с вершиной V.

темя	степень	Даже странно
	2	четное
б	2	четное
с	3	странный
d	1	странный

Четная и нечетная вершина — если степень вершины четная, вершина называется четной вершиной, а если степень вершины нечетная, вершина называется нечетной вершиной.

Степень графа . Степень графа является наибольшей степенью вершины этого графа. Для приведенного выше графа степень графа равна 3.

Лемма о рукопожатии. В графе сумма всех степеней всех вершин равна удвоенному числу ребер.

Типы графиков

Существуют различные типы графиков, которые мы изучим в следующем разделе.

Нулевой график

Нулевой граф не имеет ребер. Нулевой граф вершин $n$ обозначается через $N_n$

Простой график

Граф называется простым графом / строгим графом, если граф ненаправленный и не содержит петель или кратных ребер.

Multi-Graph

Если в графе допускается несколько ребер между одним и тем же набором вершин, это называется Multigraph. Другими словами, это граф, имеющий по крайней мере один цикл или несколько ребер.

Направленный и неориентированный граф

Граф $G = (V, E)$ называется ориентированным графом, если множество ребер составлено из упорядоченной пары вершин, а граф называется ненаправленным, если множество ребер составлено из неупорядоченной пары вершин.

Подключенный и отключенный график

Граф связен, если любые две вершины графа связаны путем; в то время как граф отключен, если хотя бы две вершины графа не соединены путем. Если граф G несвязен, то каждый максимальный связный подграф в $G$ называется связной компонентой графа $G$ .

Обычный график

Граф является регулярным, если все вершины графа имеют одинаковую степень. В регулярном графе G степени $r$ степень каждой вершины $G$ равна r.

Полный график

Граф называется полным графом, если каждые две пары вершин соединены ровно одним ребром. Полный граф с n вершинами обозначается через $K_n$

Цикл графика

Если граф состоит из одного цикла, он называется графом циклов. Граф цикла с n вершинами обозначается через $C_n$

Двудольный график

Если множество вершин графа G можно разбить на два непересекающихся множества, $V_1$ и $V_2$ , таким образом, чтобы каждое ребро графа соединяло вершину в $V_1$ с вершиной в $V_2$ , и в G нет ребер, соединяющих две вершины в $V_1$ или две вершины в $V_2$ , тогда граф $G$ называется двудольным графом.

Полный двудольный график

Полный двудольный граф — это двудольный граф, в котором каждая вершина в первом наборе соединяется с каждой отдельной вершиной во втором наборе. Полный двудольный граф обозначается через $K_ {x, y}$ , где граф $G$ содержит $x$ вершин в первом наборе и $y$ вершин во втором наборе.

Представление графиков

Есть в основном два способа представления графика —

Матрица смежности
Список смежности

Матрица смежности

Матрица смежности $A [V] [V]$ — это двумерный массив размером $V \ times V$ , где $V$ — количество вершин в неориентированном графе. Если между $V_x$ и $V_y$ имеется ребро, то значение $A [V_x] [V_y] = 1$ и $A [V_y] [V_x] = 1$ , в противном случае значение будет равно нулю. А для ориентированного графа, если существует ребро от $V_x$ до $V_y$ , тогда значение $A [V_x] [V_y] = 1$ , в противном случае значение будет равно нулю.

Матрица смежности неориентированного графа

Рассмотрим следующий неориентированный граф и построим матрицу смежности:

Матрица смежности вышеприведенного неориентированного графа будет —

		б	с	d
	0	1	1	0
б	1	0	1	0
с	1	1	0	1
d	0	0	1	0

Матрица смежности ориентированного графа

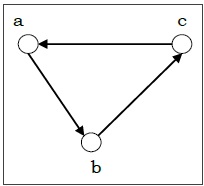
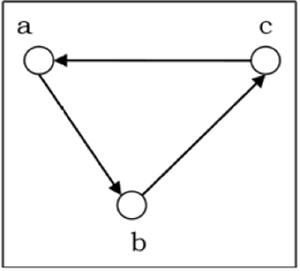
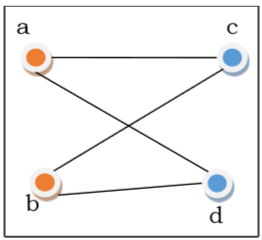
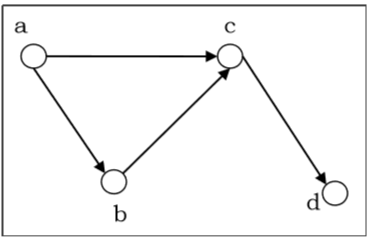
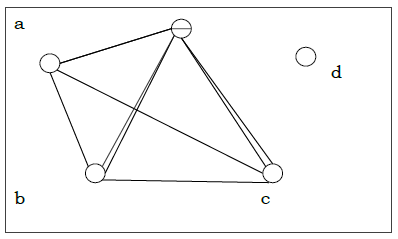
Рассмотрим следующий ориентированный граф и построим его матрицу смежности.

Матрица смежности вышеуказанного ориентированного графа будет —

		б	с	d
	0	1	1	0
б	0	0	1	0
с	0	0	0	1
d	0	0	0	0

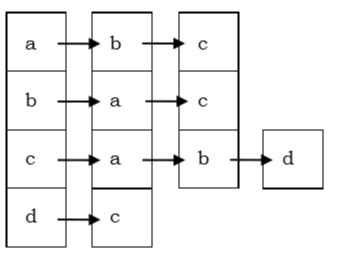
Список смежности

В списке смежности массив $(A [V])$ связанных списков используется для представления графа G с $V$ числом вершин. Запись $A [V_x]$ представляет связанный список вершин, смежных с $Vx-й$ вершиной. Список смежности неориентированного графа показан на рисунке ниже —

Планарный и непланарный граф

Планарный граф . Граф $G$ называется плоским графом, если его можно нарисовать на плоскости без пересечений ребер. Если мы рисуем граф на плоскости без пересечения ребер, это называется встраиванием графа в плоскость.

Неплоский граф — граф неплоский, если его нельзя нарисовать на плоскости без пересечения ребер графа.

изоморфизм

Если два графа G и H содержат одинаковое количество вершин, связанных одинаково, они называются изоморфными графами (обозначаемыми $G \ cong H$ ).

Легче проверить неизоморфизм, чем изоморфизм. Если выполняется любое из этих следующих условий, то два графика неизоморфны:

Количество подключенных компонентов различно
Набор вершин различен
Края кардинальности разные
Степени последовательности разные

пример

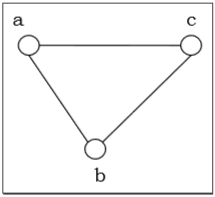
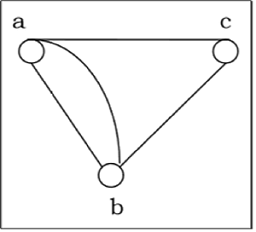
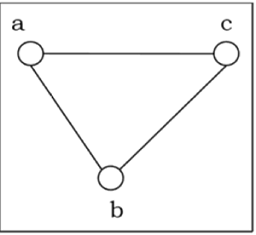
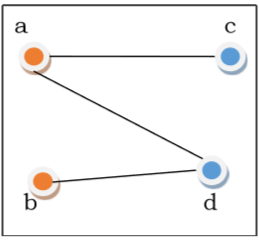
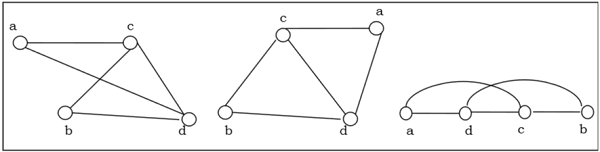
Следующие графы изоморфны —

Гомоморфизм

Гомоморфизм из графа $G$ в граф $H$ является отображением (не может быть биективным отображением) $h: G \ rightarrow H$ таким, что — $(x, y) \ in E (G) \ rightarrow (h (x), h (y)) \ in E (H)$ . Он отображает смежные вершины графа $G$ на смежные вершины графа $H$ .

Свойства гомоморфизмов

Гомоморфизм — это изоморфизм, если он является биективным отображением.
Гомоморфизм всегда сохраняет ребра и связность графа.
Композиции гомоморфизмов также являются гомоморфизмами.
Выяснить, существует ли какой-либо гомоморфный граф другого графа, является NP-полной задачей.

Гомоморфизм — это изоморфизм, если он является биективным отображением.

Гомоморфизм всегда сохраняет ребра и связность графа.

Композиции гомоморфизмов также являются гомоморфизмами.

Выяснить, существует ли какой-либо гомоморфный граф другого графа, является NP-полной задачей.

Эйлеровы графы

Связный граф $G$ называется графом Эйлера, если существует замкнутый след, включающий каждое ребро графа $G$ . Путь Эйлера — это путь, который использует каждое ребро графа ровно один раз. Путь Эйлера начинается и заканчивается в разных вершинах.

Схема Эйлера — это схема, которая использует каждое ребро графа ровно один раз. Схема Эйлера всегда начинается и заканчивается в одной и той же вершине. Связный граф $G$ является графом Эйлера тогда и только тогда, когда все вершины $G$ имеют четную степень, а связный граф $G$ эйлерова, если и только если его множество ребер можно разложить на циклы.

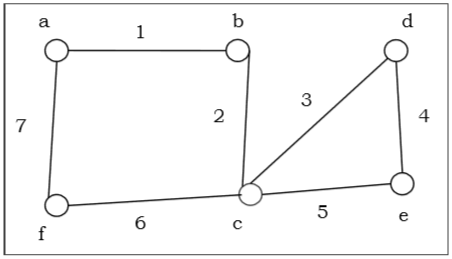
Вышеупомянутый граф является графом Эйлера как

Гамильтоновы графы

Связный граф $G$ называется гамильтоновым графом, если существует цикл, включающий каждую вершину в $G$ , и этот цикл называется гамильтоновым циклом. Гамильтоново блуждание в графе $G$ — это блуждание, которое проходит через каждую вершину ровно один раз.

Если $G$ — простой граф с n вершинами, где $n \ geq 3$ . Если $deg (v) \ geq \ frac {n} {2}$ для каждой вершины $v$ , то граф $G$ равен Гамильтонов граф. Это называется теорема Дирака .

Если $G$ — простой граф с $n$ вершинами, где $n \ geq 2$ , если $deg (x) + deg (y) \ geq n$ для каждой пары несмежных вершин x и y, то граф $G$ является гамильтоновым графом. Это называется теорема Оре .