Дискретная математика — множества

Немецкий математик Г. Кантор ввел понятие множеств. Он определил набор как набор определенных и различимых объектов, выбранных с помощью определенных правил или описания.

Теория множеств лежит в основе ряда других областей исследования, таких как теория подсчета, отношения, теория графов и конечные автоматы. В этой главе мы рассмотрим различные аспекты теории множеств .

Set — Определение

Набор представляет собой неупорядоченную коллекцию различных элементов. Множество может быть написано явно, перечисляя его элементы, используя скобку. Если порядок элементов изменяется или какой-либо элемент набора повторяется, он не вносит никаких изменений в набор.

Некоторые примеры множеств

• Набор всех натуральных чисел
• Набор всех планет в солнечной системе
• Множество всех штатов в Индии
• Набор всех строчных букв алфавита

Представление набора

Наборы могут быть представлены двумя способами —

• Реестр или Табличная форма
• Установить нотацию Builder

Реестр или Табличная форма

Набор представлен списком всех элементов, из которых он состоит. Элементы заключены в фигурные скобки и разделены запятыми.

Пример 1 — Набор гласных в английском алфавите, $A = \ lbrace a, e, i, o, u \ rbrace$

Пример 2 — Набор нечетных чисел меньше 10, $B = \ lbrace 1,3,5,7,9 \ rbrace$

Установить нотацию Builder

Набор определяется путем указания свойства, которое имеет общие элементы набора. Множество описывается как $A = \ lbrace x: p (x) \ rbrace$

Пример 1. Множество $\ lbrace a, e, i, o, u \ rbrace$ записывается как —

$A = \ lbrace x: \ text {x - гласный в английском алфавите} \ rbrace$

Пример 2 — Множество $\ lbrace 1,3,5,7,9 \ rbrace$ записывается как —

$B = \ lbrace x: 1 \ le x \ lt 10 \ and \ (x \% 2) \ ne 0 \ rbrace$

Если элемент x является членом любого множества S, он обозначается как $x \ in S$, а если элемент y не является членом множества S, он обозначается как $y \ notin S$.

Пример — если $S = \ lbrace1, 1.2, 1.7, 2 \ rbrace, 1 \ in S$, но $1.5 \ notin S$

Некоторые важные наборы

N — множество всех натуральных чисел = $\ lbrace1, 2, 3, 4, ..... \ rbrace$

Z — множество всех целых чисел = $\ lbrace ....., -3, -2, -1, 0, 1, 2, 3, ..... \ rbrace$

Z ⁺ — множество всех натуральных чисел

Q — множество всех рациональных чисел

R — множество всех действительных чисел

W — множество всех целых чисел

Мощность множества

Мощность множества S, обозначаемого $| S |$, — это количество элементов множества. Номер также называется кардинальным числом. Если множество имеет бесконечное количество элементов, его мощность равна $\ infty$.

Пример — $ | \ lbrace 1, 4, 3, 5 \ rbrace | = 4, | \ lbrace 1, 2, 3, 4, 5, \ dots \ rbrace | = \ infty $

Если есть два набора X и Y,

• $ | X | = | Y | $ обозначает два множества X и Y, имеющих одинаковую мощность. Это происходит, когда количество элементов в X точно равно числу элементов в Y. В этом случае существует биективная функция ‘f’ от X до Y.

• $ | X | \ le | Y | $ означает, что множество элементов X меньше или равно числу элементов множества Y. Это происходит, когда число элементов в X меньше или равно числу элементов в Y. Здесь существует инъективная функция ‘f’ от X до Y.

• $ | X | \ lt | Y | $ означает, что множество элементов X меньше, чем множество элементов Y. Это происходит, когда число элементов в X меньше, чем в Y. Здесь функция ‘f’ из X в Y является инъективной функцией, но не биективной.

• $ If \ | X | \ le | Y | $и$ | X | \ ge | Y | $, то$ | X | = | Y | $. Наборы X и Y обычно называют эквивалентными наборами.

$ | X | = | Y | $ обозначает два множества X и Y, имеющих одинаковую мощность. Это происходит, когда количество элементов в X точно равно числу элементов в Y. В этом случае существует биективная функция ‘f’ от X до Y.

$ | X | \ le | Y | $ означает, что множество элементов X меньше или равно числу элементов множества Y. Это происходит, когда число элементов в X меньше или равно числу элементов в Y. Здесь существует инъективная функция ‘f’ от X до Y.

$ | X | \ lt | Y | $ означает, что множество элементов X меньше, чем множество элементов Y. Это происходит, когда число элементов в X меньше, чем в Y. Здесь функция ‘f’ из X в Y является инъективной функцией, но не биективной.

$ If \ | X | \ le | Y | $и$ | X | \ ge | Y | $, то$ | X | = | Y | $. Наборы X и Y обычно называют эквивалентными наборами.

Типы Наборов

Наборы могут быть классифицированы на многие типы. Некоторые из них являются конечными, бесконечными, подмножествами, универсальными, собственными, одноэлементными множествами и т. Д.

Конечный набор

Множество, которое содержит определенное количество элементов, называется конечным множеством.

Пример — $ S = \ lbrace x \: | \: x \ in N $и$ 70 \ gt x \ gt 50 \ rbrace $

Бесконечный набор

Множество, которое содержит бесконечное количество элементов, называется бесконечным множеством.

Пример — $ S = \ lbrace x \: | \: x \ in N $и$ x \ gt 10 \ rbrace $

Подмножество

Множество X является подмножеством множества Y (записывается как $X \ subseteq Y$), если каждый элемент X является элементом множества Y.

Пример 1. Пусть $X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace$ и $Y = \ lbrace 1, 2 \ rbrace$. Здесь множество Y является подмножеством множества X, так как все элементы множества Y находятся в множестве X. Следовательно, мы можем написать $Y \ subseteq X$.

Пример 2. Пусть $X = \ lbrace 1, 2, 3 \ rbrace$ и $Y = \ lbrace 1, 2, 3 \ rbrace$. Здесь множество Y — это подмножество (не правильное подмножество) множества X, так как все элементы множества Y находятся в множестве X. Следовательно, мы можем записать $Y \ subseteq X$.

Правильное подмножество

Термин «правильное подмножество» может быть определен как «подмножество, но не равно». Набор X является собственным подмножеством множества Y (записывается как $X \ subset Y$), если каждый элемент X является элементом множества Y и $ | X | \ lt | Y | $.

Пример. Пусть $X = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace$ и $Y = \ lbrace 1, 2 \ rbrace$. Здесь установите $Y \ subset X$, так как все элементы в $Y$ также содержатся в $X$, и $X$ имеет хотя бы один элемент больше, чем набор $Y$.

Универсальный комплект

Это коллекция всех элементов в определенном контексте или приложении. Все наборы в этом контексте или приложении по существу являются подмножествами этого универсального набора. Универсальные множества представлены как $U$.

Пример. Мы можем определить $U$ как совокупность всех животных на земле. В этом случае множество всех млекопитающих — это подмножество $U$, множество всех рыб — это подмножество $U$, множество всех насекомых — это подмножество $U$ и так далее.

Пустой набор или нулевой набор

Пустой набор не содержит элементов. Обозначается $\ emptyset$. Поскольку число элементов в пустом множестве конечно, пустое множество является конечным множеством. Мощность пустого набора или нулевого набора равна нулю.

Пример — $ S = \ lbrace x \: | \: x \ in N $и$ 7 \ lt x \ lt 8 \ rbrace = \ emptyset $

Синглтон или блок

Одиночный набор или единичный набор содержит только один элемент. Одноэлементное множество обозначается через $\ lbrace s \ rbrace$.

Пример — $ S = \ lbrace x \: | \: x \ in N, \ 7 \ lt x \ lt 9 \ rbrace $=$ \ lbrace 8 \ rbrace $

Равный Набор

Если два набора содержат одинаковые элементы, они называются равными.

Пример — если $A = \ lbrace 1, 2, 6 \ rbrace$ и $B = \ lbrace 6, 1, 2 \ rbrace$, они равны, так как каждый элемент множества A является элементом множества B и каждым элементом множество B является элементом множества A.

Эквивалентный набор

Если мощности двух множеств одинаковы, они называются эквивалентными множествами.

Пример. Если $A = \ lbrace 1, 2, 6 \ rbrace$ и $B = \ lbrace 16, 17, 22 \ rbrace$, они эквивалентны, поскольку мощность A равна мощности B. ie $ | A | = | B | = 3 $

Набор перекрывающихся

Два набора, которые имеют хотя бы один общий элемент, называются перекрывающимися наборами.

В случае перекрывающихся наборов —

• $n (A \ cup B) = n (A) + n (B) - n (A \ cap B)$

• $n (A \ cup B) = n (A - B) + n (B - A) + n (A \ cap B)$

• $n (A) = n (A - B) + n (A \ cap B)$

• $n (B) = n (B - A) + n (A \ cap B)$

$n (A \ cup B) = n (A) + n (B) - n (A \ cap B)$

$n (A \ cup B) = n (A - B) + n (B - A) + n (A \ cap B)$

$n (A) = n (A - B) + n (A \ cap B)$

$n (B) = n (B - A) + n (A \ cap B)$

Пример. Пусть $A = \ lbrace 1, 2, 6 \ rbrace$ и $B = \ lbrace 6, 12, 42 \ rbrace$. Существует общий элемент «6», поэтому эти наборы являются перекрывающимися.

Несвязанный набор

Два набора A и B называются непересекающимися, если они не имеют хотя бы одного общего элемента. Следовательно, непересекающиеся множества обладают следующими свойствами:

• $n (A \ cap B) = \ emptyset$

• $n (A \ cup B) = n (A) + n (B)$

$n (A \ cap B) = \ emptyset$

$n (A \ cup B) = n (A) + n (B)$

Пример — Пусть, $A = \ lbrace 1, 2, 6 \ rbrace$ и $B = \ lbrace 7, 9, 14 \ rbrace$, не существует ни одного общего элемента, поэтому эти наборы являются перекрывающимися.

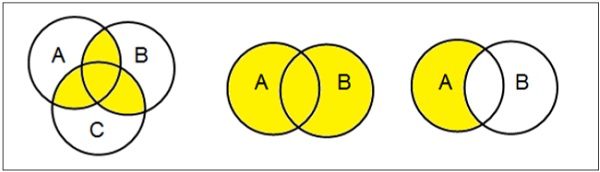
Диаграммы Венна

Диаграмма Венна, изобретенная в 1880 году Джоном Венном, является схематической диаграммой, которая показывает все возможные логические связи между различными математическими наборами.

Примеры

Операции над множествами

Операции над множествами включают в себя объединение множеств, пересечение множеств, разность множеств, дополнение множества и декартово произведение.

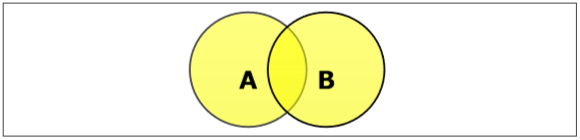
Установить Союз

Объединение множеств A и B (обозначается как $A \ cup B$) — это множество элементов, которые находятся в A, в B или в A и B. Следовательно, $ A \ cup B = \ lbrace x \: | \: x \ in A \ OR \ x \ in B \ rbrace $.

Пример. Если $A = \ lbrace 10, 11, 12, 13 \ rbrace$ и B = $\ lbrace 13, 14, 15 \ rbrace$, то $A \ cup B = \ lbrace 10, 11, 12, 13, 14, 15$. (Общий элемент встречается только один раз)

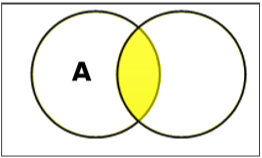
Установить пересечение

Пересечение множеств A и B (обозначается как $A \ cap B$) — это множество элементов, которые находятся в A и B. Следовательно, A capB= lbracex|x вA AND x inB rbrace$A \ cap B = \ lbrace x \: | \: x \ в A \ AND \ x \ in B \ rbrace$.

Пример. Если $A = \ lbrace 11, 12, 13 \ rbrace$ и $B = \ lbrace 13, 14, 15 \ rbrace$, то $A \ cap B = \ lbrace 13 \ rbrace$.

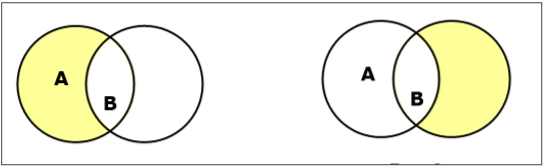
Установить разницу / относительное дополнение

Разность множеств множеств A и B (обозначаемая $A - B$) — это множество элементов, которые находятся только в A, но не в B. Следовательно, $ A — B = \ lbrace x \: | \: x \ in A \ AND \ x \ notin B \ rbrace $.

Пример. Если $A = \ lbrace 10, 11, 12, 13 \ rbrace$ и $B = \ lbrace 13, 14, 15 \ rbrace$, то $(A - B) = \ lbrace 10, 11, 12 \ rbrace$ и $(B - A) = \ lbrace 14, 15 \ rbrace$. Здесь мы можем увидеть $(A - B) \ ne (B - A)$

Дополнение набора

Дополнением к множеству A (обозначаемому $A '$) является множество элементов, не входящих в множество A. Следовательно, $ A’ = \ lbrace x | x \ notin A \ rbrace $.

В частности, $A '= (U - A)$, где $U$ — универсальное множество, которое содержит все объекты.

Пример — если $ A = \ lbrace x \: | \: x \ \: {принадлежит \: к \: множеству \: из \: нечетных \: целых чисел} \ rbrace $then$ A ‘= \ lbrace y \: | \: y \ \: {не \: не \: принадлежат \: к \: набору \: of \: нечетные \: целые числа} \ rbrace $

Декартово произведение / кросс произведение

Декартово произведение n числа множеств $A_1, A_2, \ dots A_n$, обозначаемого как $A_1 \ times A_2 \ dots \ times A_n$, может быть определено как все возможные упорядоченные пары $(x_1, x_2, \ dots x_n)$, где $x_1 \ in A_1, x_2 \ in A_2, \ dots x_n \ in A_n$

Пример — Если мы возьмем два набора $A = \ lbrace a, b \ rbrace$ и $B = \ lbrace 1, 2 \ rbrace$,

Декартово произведение A и B записывается в виде — $A \ times B = \ lbrace (a, 1), (a, 2), (b, 1), (b, 2) \ rbrace$

Декартово произведение B и A записывается в виде — $B \ times A = \ lbrace (1, a), (1, b), (2, a), (2, b) \ rbrace$

Набор питания

Набор мощности набора S — это набор всех подмножеств S, включая пустой набор. Мощность множества степеней множества S мощности n равна $2 ^ n$. Набор мощности обозначается как $P (S)$.

Пример —

Для множества $S = \ lbrace a, b, c, d \ rbrace$ вычислим подмножества —

• Подмножества с 0 элементами — $\ lbrace \ emptyset \ rbrace$ (пустой набор)

• Подмножества с 1 элементом — $\ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace$

• Подмножества с 2 элементами — $\ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace$

• Подмножества с 3 элементами — $\ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace$

• Подмножества с 4 элементами — $\ lbrace a, b, c, d \ rbrace$

Подмножества с 0 элементами — $\ lbrace \ emptyset \ rbrace$ (пустой набор)

Подмножества с 1 элементом — $\ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace$

Подмножества с 2 элементами — $\ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace$

Подмножества с 3 элементами — $\ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace$

Подмножества с 4 элементами — $\ lbrace a, b, c, d \ rbrace$

Следовательно, $P (S) =$

$\ lbrace \ quad \ lbrace \ emptyset \ rbrace, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ lbrace c \ rbrace, \ lbrace d \ rbrace, \ lbrace a, b \ rbrace, \ lbrace a, c \ rbrace, \ lbrace a, d \ rbrace, \ lbrace b, c \ rbrace, \ lbrace b, d \ rbrace, \ lbrace c, d \ rbrace, \ lbrace a, b, c \ rbrace, \ lbrace a, b, d \ rbrace, \ lbrace a, c, d \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace a, b, c, d \ rbrace \ quad \ rbrace$

$ | P (S) | = 2 ^ 4 = 16 $

Примечание. Набор мощности пустого набора также является пустым набором.

$ | P (\ lbrace \ emptyset \ rbrace) | = 2 ^ 0 = 1 $

Разделение набора

Разделение множества, скажем, S , представляет собой набор из n непересекающихся подмножеств, скажем, $P_1, P_2, \ dots P_n$, который удовлетворяет следующим трем условиям:

• $P_i$ не содержит пустого набора.

  $\ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack$

• Объединение подмножеств должно равняться всему исходному набору.

  $\ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack$

• Пересечение любых двух различных множеств пусто.

   lbrackPa capPb= lbrace emptyset rbrace, for a neb where n gea,b ge0 rbrack$\ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \ where \ n \ ge a, \: b \ ge 0 \ rbrack$

$P_i$ не содержит пустого набора.

$\ lbrack P_i \ ne \ lbrace \ emptyset \ rbrace \ for \ all \ 0 \ lt i \ le n \ rbrack$

Объединение подмножеств должно равняться всему исходному набору.

$\ lbrack P_1 \ cup P_2 \ cup \ dots \ cup P_n = S \ rbrack$

Пересечение любых двух различных множеств пусто.

 lbrackPa capPb= lbrace emptyset rbrace, for a neb where n gea,b ge0 rbrack$\ lbrack P_a \ cap P_b = \ lbrace \ emptyset \ rbrace, \ for \ a \ ne b \ where \ n \ ge a, \: b \ ge 0 \ rbrack$

пример

Пусть $S = \ lbrace a, b, c, d, e, f, g, h \ rbrace$

Одним из вероятных разбиений является $\ lbrace a \ rbrace, \ lbrace b, c, d \ rbrace, \ lbrace e, f, g, h \ rbrace$

Другим вероятным разбиением является $\ lbrace a, b \ rbrace, \ lbrace c, d \ rbrace, \ lbrace e, f, g, h \ rbrace$

Белл номера

Числа в колокольчиках подсчитывают количество способов разбить набор. Они обозначаются через $B_n$, где n — мощность множества.

Пример —

Пусть $S = \ lbrace 1, 2, 3 \ rbrace$, $ n = | S | = 3 $

Альтернативные разделы —

1. $\ emptyset, \ lbrace 1, 2, 3 \ rbrace$

2. $\ lbrace 1 \ rbrace, \ lbrace 2, 3 \ rbrace$

3. $\ lbrace 1, 2 \ rbrace, \ lbrace 3 \ rbrace$

4. $\ lbrace 1, 3 \ rbrace, \ lbrace 2 \ rbrace$

5. $\ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace$

Следовательно, $B_3 = 5$