Обратное распространение реализуется в средах глубокого обучения, таких как Tensorflow, Torch, Theano и т. Д., С использованием вычислительных графов. Что еще более важно, понимание обратного распространения на вычислительных графах сочетает в себе несколько различных алгоритмов и их вариаций, таких как backprop по времени и backprop с общими весами. Как только все преобразуется в вычислительный граф, они остаются тем же алгоритмом — просто обратное распространение на вычислительных графах.
Что такое вычислительный граф
Вычислительный граф определяется как ориентированный граф, где узлы соответствуют математическим операциям. Вычислительные графики — это способ выражения и оценки математического выражения.
Например, вот простое математическое уравнение —
$$ p = x + y $$
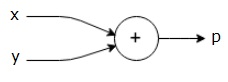
Мы можем нарисовать расчетный график вышеприведенного уравнения следующим образом.
Вышеупомянутый вычислительный граф имеет узел сложения (узел со знаком «+») с двумя входными переменными x и y и одним выходным q.
Давайте возьмем другой пример, немного более сложный. У нас есть следующее уравнение.
$$ g = \ left (x + y \ right) \ ast z $$
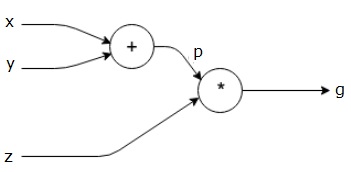
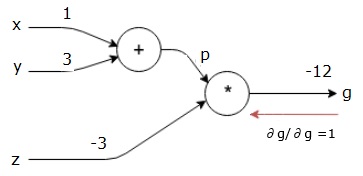
Вышеупомянутое уравнение представлено следующим вычислительным графиком.
Вычислительные графики и обратное распространение
Вычислительные графики и обратное распространение, оба являются важными основными понятиями в глубоком обучении для обучения нейронных сетей.
Форвард Пасс
Прямой проход — это процедура оценки значения математического выражения, представленного вычислительными графами. Выполнение прямого прохода означает, что мы передаем значение из переменных в прямом направлении слева (вход) вправо, где вывод.
Давайте рассмотрим пример, дав некоторую ценность всем входам. Предположим, следующие значения даны для всех входов.
$$ x = 1, y = 3, z = −3 $$
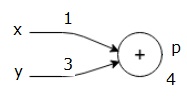
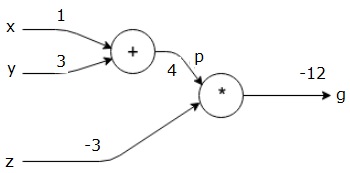
Передавая эти значения на входы, мы можем выполнить прямой переход и получить следующие значения для выходов на каждом узле.
Сначала мы используем значения x = 1 и y = 3, чтобы получить p = 4.
Затем мы используем p = 4 и z = -3, чтобы получить g = -12. Идем слева направо, вперед.
Цели обратного прохода
В обратном проходе наше намерение состоит в том, чтобы вычислить градиенты для каждого входа относительно конечного результата. Эти градиенты необходимы для обучения нейронной сети с использованием градиентного спуска.
Например, мы хотим следующие градиенты.
Желаемые градиенты
$$ \ frac {\ частичный х} {\ частичный ф}, \ frac {\ частичный у} {\ частичный ф}, \ frac {\ частичный г} {\ частичный ф} $$
Обратный проход (обратное распространение)
Мы начинаем обратный проход, находя производную конечного результата по конечному результату (самому!). Таким образом, это приведет к выводу идентичности, и значение будет равно единице.
$$ \ frac {\ частичный г} {\ частичный г} = 1 $$
Наш вычислительный график теперь выглядит так, как показано ниже —
Далее мы сделаем обратный проход через операцию «*». Мы рассчитаем градиенты в точках p и z. Поскольку g = p * z, мы знаем, что —
$$ \ frac {\ частичный г} {\ частичный г} = p $$
$$ \ frac {\ частичный г} {\ частный р} = z $$
Мы уже знаем значения z и p из прямого прохода. Следовательно, мы получаем —
$$ \ frac {\ частичный г} {\ частичный г} = p = 4 $$
а также
$$ \ frac {\ частичный г} {\ частичный р} = z = -3 $$
Мы хотим рассчитать градиенты в х и у —
$$ \ frac {\ частичный г} {\ частичный х}, \ frac {\ частичный г} {\ частичный г} $$
Однако мы хотим сделать это эффективно (хотя x и g на этом графике находятся всего в двух шагах, представьте, что они действительно далеки друг от друга). Чтобы эффективно рассчитать эти значения, мы будем использовать цепное правило дифференцирования. Из правила цепочки имеем:
$$ \ frac {\ частичный г} {\ частичный х} = \ фрак {\ частичный г} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный х} $$
$$ \ frac {\ частичный г} {\ частичный y} = \ frac {\ частичный г} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный у} $$
Но мы уже знаем, что dg / dp = -3, dp / dx и dp / dy просты, так как p напрямую зависит от x и y. У нас есть —
$$ p = x + y \ Rightarrow \ frac {\ частичный x} {\ частичный p} = 1, \ frac {\ частичный y} {\ частичный p} = 1 $$
Следовательно, мы получаем —
$$ \ frac {\ частичный г} {\ частичный ф} = \ частичный {} частичный г} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный х} = \ левый (-3 \ правый) .1 = -3 $$
Кроме того, для ввода у —
$$ \ frac {\ частичный г} {\ частичный у} = \ частичный {} частичный} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный у} = \ левый (-3 \ правый) .1 = -3 $$
Основная причина сделать это в обратном направлении заключается в том, что когда нам нужно было вычислить градиент в точке x, мы использовали только уже вычисленные значения и dq / dx (производная от вывода узла по отношению к входу того же узла). Мы использовали локальную информацию для вычисления глобального значения.
Шаги для обучения нейронной сети
Выполните следующие шаги для обучения нейронной сети —
Для точки данных x в наборе данных мы передаем передачу с x в качестве входных данных и рассчитаем стоимость c в качестве выходных данных.
Мы делаем обратный проход, начиная с c, и вычисляем градиенты для всех узлов в графе. Это включает в себя узлы, которые представляют веса нейронной сети.
Затем мы обновляем вес, выполняя W = W — скорость обучения * градиенты.
Мы повторяем этот процесс, пока не будут выполнены критерии остановки.