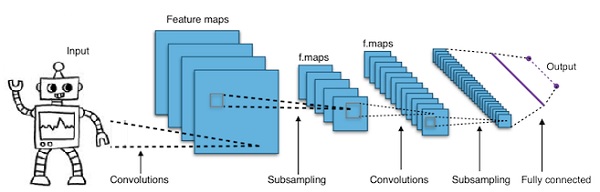
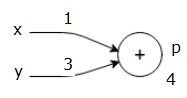
Python Deep Learning — Введение

Короче говоря, глубокое структурированное обучение или иерархическое обучение или глубокое обучение является частью семейства методов машинного обучения, которые сами являются подмножеством более широкой области искусственного интеллекта.

Глубокое обучение — это класс алгоритмов машинного обучения, которые используют несколько уровней нелинейных блоков обработки для извлечения и преобразования признаков. Каждый последующий слой использует выходные данные предыдущего слоя в качестве входных данных.

Глубокие нейронные сети, сети глубоких убеждений и рекуррентные нейронные сети применяются в таких областях, как компьютерное зрение, распознавание речи, обработка естественного языка, распознавание звука, фильтрация в социальных сетях, машинный перевод и биоинформатика, где они дают результаты, сопоставимые и в некоторых случаях лучше, чем человеческие эксперты.

Алгоритмы глубокого обучения и сети —

• основаны на неконтролируемом изучении нескольких уровней функций или представлений данных. Элементы более высокого уровня выводятся из элементов более низкого уровня для формирования иерархического представления.

• использовать некоторую форму градиентного спуска для обучения.

основаны на неконтролируемом изучении нескольких уровней функций или представлений данных. Элементы более высокого уровня выводятся из элементов более низкого уровня для формирования иерархического представления.

использовать некоторую форму градиентного спуска для обучения.

Python Deep Learning — Окружающая среда

В этой главе мы узнаем о среде, настроенной для глубокого обучения Python. Мы должны установить следующее программное обеспечение для создания алгоритмов глубокого обучения.

• Python 2.7+
• Сципи с Нампи
• Matplotlib
• Theano
• Keras
• TensorFlow

Настоятельно рекомендуется установить Python, NumPy, SciPy и Matplotlib через дистрибутив Anaconda. Он поставляется со всеми этими пакетами.

Мы должны убедиться, что различные типы программного обеспечения установлены правильно.

Давайте перейдем к нашей программе командной строки и наберем следующую команду —

$ python
Python 3.6.3 |Anaconda custom (32-bit)| (default, Oct 13 2017, 14:21:34)
[GCC 7.2.0] on linux

Далее мы можем импортировать необходимые библиотеки и распечатать их версии —

import numpy
print numpy.__version__

Выход

1.14.2

Установка Theano, TensorFlow и Keras

Прежде чем мы начнем с установки пакетов — Theano, TensorFlow и Keras, мы должны подтвердить, установлен ли pip . Система управления пакетами в Anaconda называется pip.

Чтобы подтвердить установку pip, введите в командной строке следующее:

$ pip

Как только установка pip будет подтверждена, мы можем установить TensorFlow и Keras, выполнив следующую команду:

$pip install theano
$pip install tensorflow
$pip install keras

Подтвердите установку Theano, выполнив следующую строку кода:

$python –c “import theano: print (theano.__version__)”

Выход

1.0.1

Подтвердите установку Tensorflow, выполнив следующую строку кода:

$python –c “import tensorflow: print tensorflow.__version__”

Выход

1.7.0

Подтвердите установку Keras, выполнив следующую строку кода:

$python –c “import keras: print keras.__version__”
Using TensorFlow backend

Выход

2.1.5

Python Deep Basic Машинное обучение

Искусственный интеллект (ИИ) — это любой код, алгоритм или метод, который позволяет компьютеру имитировать когнитивное поведение или интеллект человека. Машинное обучение (ML) — это подмножество ИИ, в котором используются статистические методы, позволяющие машинам учиться и совершенствоваться с опытом. Глубокое обучение — это подмножество машинного обучения, которое делает возможным вычисление многослойных нейронных сетей. Машинное обучение рассматривается как поверхностное обучение, а глубокое обучение — как иерархическое обучение с абстракцией.

Машинное обучение имеет дело с широким спектром понятий. Концепции перечислены ниже —

• контролируемый
• бесконтрольный
• обучение подкреплению
• линейная регрессия
• функции стоимости
• переобучения
• под облегающим
• гиперпараметр и др.

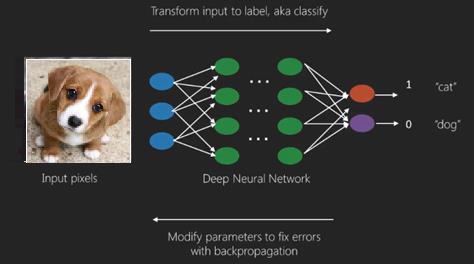
При контролируемом обучении мы учимся прогнозировать значения на основе помеченных данных. Один метод ML, который помогает здесь, — это классификация, где целевые значения являются дискретными значениями; например, кошки и собаки. Другая техника в машинном обучении, которая может помочь, — это регрессия. Регрессия работает на целевых значениях. Целевые значения являются непрерывными значениями; например, данные фондового рынка могут быть проанализированы с использованием регрессии.

При неконтролируемом обучении мы делаем выводы из входных данных, которые не обозначены или не структурированы. Если у нас есть миллион медицинских карт, и мы должны разобраться в этом, найти основную структуру, выбросы или обнаружить аномалии, мы используем метод кластеризации для разделения данных на широкие кластеры.

Наборы данных делятся на обучающие наборы, наборы для тестирования, наборы для проверки и так далее.

Прорыв в 2012 году принес концепцию глубокого обучения в известность. Алгоритм успешно разделил 1 миллион изображений на 1000 категорий, используя 2 графических процессора и такие новейшие технологии, как Big Data.

Глубокое обучение и традиционное машинное обучение

Одной из основных проблем, с которыми сталкиваются в традиционных моделях машинного обучения, является процесс, называемый извлечением признаков. Программист должен быть конкретным и сообщать компьютеру о функциях, на которые нужно обратить внимание. Эти функции помогут в принятии решений.

Ввод необработанных данных в алгоритм редко работает, поэтому извлечение функций является важной частью традиционного рабочего процесса машинного обучения.

Это накладывает огромную ответственность на программиста, и эффективность алгоритма во многом зависит от того, насколько изобретателен программист. Для сложных проблем, таких как распознавание объектов или почерк, это огромная проблема.

Глубокое обучение с возможностью изучения нескольких уровней представления — это один из немногих методов, который помог нам с автоматическим извлечением признаков. Можно предположить, что нижние уровни выполняют автоматическое извлечение элементов, практически не требуя указания со стороны программиста.

Искусственные нейронные сети

Искусственная нейронная сеть, или, если коротко, просто нейронная сеть, не новая идея. Это было около 80 лет.

Только в 2011 году Deep Neural Networks стали популярными благодаря использованию новых методов, огромной доступности наборов данных и мощных компьютеров.

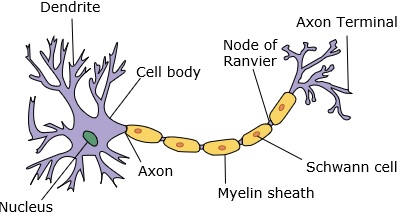
Нейронная сеть имитирует нейрон с дендритами, ядром, аксоном и терминальным аксоном.

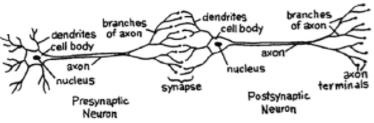
Для сети нам нужны два нейрона. Эти нейроны передают информацию через синапс между дендритами одного и конечным аксоном другого.

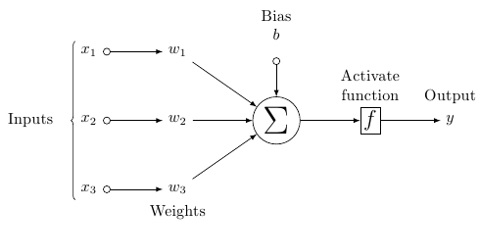
Вероятная модель искусственного нейрона выглядит следующим образом —

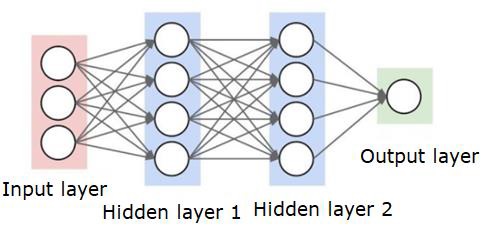
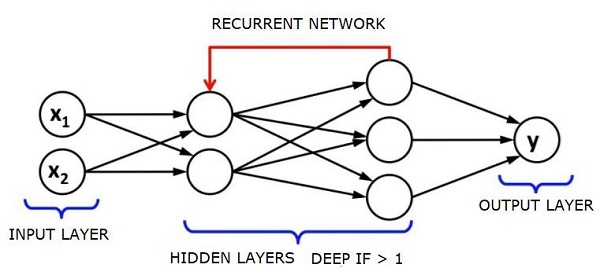
Нейронная сеть будет выглядеть так, как показано ниже —

Кружки — это нейроны или узлы, с их функциями в отношении данных, а соединяющие их линии / ребра являются весами / информацией, передаваемой по ней.

Каждый столбец является слоем. Первый слой ваших данных является входным слоем. Затем все слои между входным слоем и выходным слоем являются скрытыми слоями.

Если у вас есть один или несколько скрытых слоев, то у вас неглубокая нейронная сеть. Если у вас много скрытых слоев, значит, у вас глубокая нейронная сеть.

В этой модели у вас есть входные данные, вы взвешиваете их и пропускаете через функцию в нейроне, которая называется пороговой функцией или функцией активации.

По сути, это сумма всех значений после сравнения с определенным значением. Если вы подаете сигнал, то результат будет (1) или ничего не сработает, тогда (0). Затем он взвешивается и передается следующему нейрону, и запускается такая же функция.

Мы можем иметь сигмовидную (s-образную) функцию в качестве функции активации.

Что касается весов, они просто случайны для начала, и они уникальны для каждого входа в узел / нейрон.

В типичном «прямом канале», самом базовом типе нейронной сети, ваша информация передается прямо через созданную вами сеть, и вы сравниваете выходные данные с тем, на что, как вы надеялись, будут использоваться ваши примерные данные.

Отсюда вам нужно отрегулировать веса, чтобы помочь вам получить ваш вывод, чтобы соответствовать желаемому результату.

Отправка данных напрямую через нейронную сеть называется нейронной сетью с прямой связью.

Наши данные идут от ввода к слоям, по порядку, а затем к выводу.

Когда мы возвращаемся назад и начинаем корректировать веса, чтобы минимизировать потери / затраты, это называется обратным распространением.

Это проблема оптимизации. В реальной нейронной сети нам приходится иметь дело с сотнями тысяч переменных, или миллионами, или более.

Первым решением было использование стохастического градиентного спуска в качестве метода оптимизации. Теперь есть такие опции, как AdaGrad, Adam Optimizer и так далее. В любом случае, это масштабная вычислительная операция. Именно поэтому нейронные сети в основном оставались на полке более полувека. Лишь совсем недавно у нас даже была мощь и архитектура в наших машинах, чтобы даже рассмотреть возможность выполнения этих операций, и наборы данных надлежащего размера, чтобы соответствовать.

Для простых задач классификации нейронная сеть относительно близка по производительности к другим простым алгоритмам, таким как K Nearest Neighbours. Реальная полезность нейронных сетей осознается, когда у нас гораздо больше данных и гораздо более сложные вопросы, которые превосходят другие модели машинного обучения.

Глубокие Нейронные Сети

Глубокая нейронная сеть (DNN) — это ANN с несколькими скрытыми слоями между входным и выходным слоями. Подобно мелким ANN, DNN могут моделировать сложные нелинейные отношения.

Основная цель нейронной сети состоит в том, чтобы получать набор входных данных, выполнять прогрессивно сложные вычисления и предоставлять выходные данные для решения реальных задач, таких как классификация. Мы ограничиваем себя для продвижения вперед нейронных сетей.

У нас есть вход, выход и поток последовательных данных в глубокой сети.

Нейронные сети широко используются в контролируемых задачах обучения и обучения. Эти сети основаны на наборе слоев, соединенных друг с другом.

При глубоком обучении количество скрытых слоев, в основном нелинейных, может быть большим; скажем около 1000 слоев.

Модели DL дают гораздо лучшие результаты, чем обычные сети ML.

В основном мы используем метод градиентного спуска для оптимизации сети и минимизации функции потерь.

Мы можем использовать Imagenet , хранилище миллионов цифровых изображений, чтобы классифицировать набор данных по категориям, таким как кошки и собаки. Сети DL все чаще используются для динамических изображений, кроме статических, а также для анализа временных рядов и текста.

Обучение наборов данных является важной частью моделей глубокого обучения. Кроме того, Backpropagation является основным алгоритмом обучения моделей DL.

DL занимается обучением больших нейронных сетей со сложными преобразованиями ввода-вывода.

Одним из примеров DL является сопоставление фотографии с именем человека (-ов) на фотографии, как это происходит в социальных сетях, и описание фотографии с помощью фразы — еще одно недавнее применение DL.

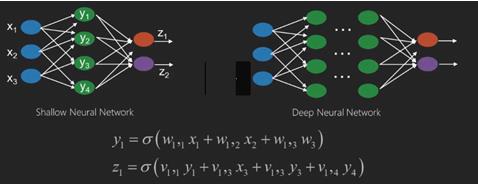
Нейронные сети — это функции, которые имеют входы, такие как x1, x2, x3…, которые преобразуются в выходы, такие как z1, z2, z3 и т. Д., В две (мелкие сети) или в несколько промежуточных операций, также называемых слоями (глубокие сети).

Веса и уклоны меняются от слоя к слою. «w» и «v» являются весами или синапсами слоев нейронных сетей.

Лучший вариант глубокого обучения — это контролируемая проблема обучения. Здесь у нас есть большой набор входных данных с желаемым набором выходных данных.

Здесь мы применяем алгоритм обратного распространения для получения правильного прогноза на выходе.

Самым базовым набором данных для глубокого изучения является MNIST, набор рукописных цифр.

Мы можем обучить глубокую сверточную нейронную сеть с Keras, чтобы классифицировать изображения рукописных цифр из этого набора данных.

Увольнение или активация классификатора нейронной сети дает оценку. Например, чтобы классифицировать пациентов как больных и здоровых, мы учитываем такие параметры, как рост, вес и температура тела, артериальное давление и т. Д.

Высокий балл означает, что пациент болен, а низкий балл означает, что он здоров.

Каждый узел в выходном и скрытом слоях имеет свои классификаторы. Входной слой получает входные данные и передает свои оценки следующему скрытому слою для дальнейшей активации, и это продолжается до тех пор, пока не будет достигнут вывод.

Этот прогресс от входа к выходу слева направо в прямом направлении называется прямым распространением.

Путь кредитного присвоения (CAP) в нейронной сети — это последовательность преобразований, начинающихся от входа к выходу. САР вырабатывают возможные причинно-следственные связи между входом и выходом.

Глубина CAP для данной нейронной сети с прямой связью или глубина CAP — это количество скрытых слоев плюс один в качестве выходного слоя. Для рекуррентных нейронных сетей, где сигнал может распространяться через слой несколько раз, глубина CAP может быть потенциально безгранична.

Глубокие сети и мелкие сети

Нет четкого порога глубины, который отделяет мелкое обучение от глубокого обучения; но в основном согласны, что для глубокого обучения, которое имеет несколько нелинейных уровней, CAP должен быть больше двух.

Базовый узел в нейронной сети — это восприятие, имитирующее нейрон в биологической нейронной сети. Тогда у нас есть многослойное восприятие или MLP. Каждый набор входов модифицируется набором весов и смещений; каждое ребро имеет уникальный вес, а каждый узел имеет уникальный уклон.

Точность предсказания нейронной сети зависит от ее веса и смещения.

Процесс повышения точности нейронной сети называется обучением. Выходной сигнал из прямой сети поддержки сравнивается с тем значением, которое, как известно, является правильным.

Функция затрат или функция потерь — это разница между сгенерированным и фактическим выходом.

Смысл обучения заключается в том, чтобы сделать затраты на обучение как можно меньшими на миллионах примеров обучения. Для этого сеть изменяет веса и смещения до тех пор, пока прогноз не будет соответствовать правильному результату.

После хорошей подготовки нейронная сеть может каждый раз делать точный прогноз.

Когда шаблон становится сложным и вы хотите, чтобы ваш компьютер распознал их, вы должны использовать нейронные сети. В таких сложных сценариях шаблонов нейронная сеть превосходит все конкурирующие алгоритмы.

В настоящее время существуют графические процессоры, которые могут обучать их быстрее, чем когда-либо прежде. Глубокие нейронные сети уже революционизируют область ИИ

Компьютеры хорошо зарекомендовали себя, выполняя повторяющиеся вычисления и следуя подробным инструкциям, но не очень хорошо распознавали сложные шаблоны.

Если существует проблема распознавания простых шаблонов, то машина опорных векторов (svm) или классификатор логистической регрессии могут хорошо справиться с этой задачей, но, поскольку сложность шаблонов возрастает, нет другого выхода, кроме как перейти к глубоким нейронным сетям.

Поэтому для сложных моделей, таких как человеческое лицо, мелкие нейронные сети терпят неудачу и не имеют альтернативы, кроме как перейти к глубоким нейронным сетям с большим количеством слоев. Глубокие сети могут выполнять свою работу, разбивая сложные шаблоны на более простые. Например, человеческое лицо; Адепская сеть использовала бы края, чтобы обнаружить такие части, как губы, нос, глаза, уши и т. д., а затем объединить их вместе, чтобы сформировать человеческое лицо

Точность правильного предсказания стала настолько точной, что в последнее время на конкурсе Google Pattern Recognition Challenge человек сильно ударил.

Эта идея сети слоистых персептронов была известна уже давно; в этой области глубокие сети имитируют человеческий мозг. Но одним из недостатков этого является то, что они занимают много времени на обучение, аппаратное ограничение

Однако недавние высокопроизводительные графические процессоры смогли обучить такие глубокие сети менее чем за неделю; в то время как быстрый процессор мог сделать недели или месяцы, чтобы сделать то же самое.

Выбор глубокой сети

Как выбрать глубокую сеть? Мы должны решить, строим ли мы классификатор или пытаемся найти шаблоны в данных, и будем ли мы использовать обучение без контроля. Чтобы извлечь шаблоны из набора немаркированных данных, мы используем ограниченную машину Больцмана или автоматический кодировщик.

При выборе глубокой сети учитывайте следующие моменты:

• Для обработки текста, анализа настроений, анализа и распознавания имен мы используем рекуррентную сеть или рекурсивную нейронную тензорную сеть или RNTN;

• Для любой языковой модели, которая работает на уровне символов, мы используем рекуррентную сеть.

• Для распознавания изображений мы используем глубокую веру в сеть DBN или сверточную сеть.

• Для распознавания объектов мы используем RNTN или сверточную сеть.

• Для распознавания речи мы используем рекуррентную сеть.

Для обработки текста, анализа настроений, анализа и распознавания имен мы используем рекуррентную сеть или рекурсивную нейронную тензорную сеть или RNTN;

Для любой языковой модели, которая работает на уровне символов, мы используем рекуррентную сеть.

Для распознавания изображений мы используем глубокую веру в сеть DBN или сверточную сеть.

Для распознавания объектов мы используем RNTN или сверточную сеть.

Для распознавания речи мы используем рекуррентную сеть.

В целом, сети глубокого убеждения и многослойные персептроны с выпрямленными линейными единицами или RELU являются хорошими вариантами классификации.

Для анализа временных рядов всегда рекомендуется использовать рекуррентную сеть.

Нейронные сети существуют уже более 50 лет; но только теперь они стали заметными. Причина в том, что их трудно тренировать; Когда мы пытаемся обучить их с помощью метода, называемого обратным распространением, мы сталкиваемся с проблемой, называемой исчезновением или взрывом градиентов. Когда это происходит, обучение занимает больше времени, а точность отходит на второй план. При обучении набора данных мы постоянно вычисляем функцию стоимости, которая является разницей между прогнозируемым результатом и фактическим выходом из набора маркированных данных обучения. Затем функция стоимости минимизируется путем корректировки значений весов и смещений до самого низкого значения получается. В тренировочном процессе используется градиент, который представляет собой скорость, с которой стоимость будет изменяться по отношению к изменению значений веса или смещения.

Ограниченные сети Больцмана или автоэнкодеры — RBN

В 2006 году был достигнут прорыв в решении проблемы исчезающих градиентов. Джефф Хинтон разработал новую стратегию, которая привела к разработке Restricted Boltzman Machine — RBM , мелкой двухслойной сетки.

Первый слой — это видимый слой, а второй слой — это скрытый слой. Каждый узел в видимом слое связан с каждым узлом в скрытом слое. Сеть известна как ограниченная, так как никаким двум уровням в пределах одного уровня не разрешено совместно использовать соединение.

Автоэнкодеры — это сети, которые кодируют входные данные как векторы. Они создают скрытое или сжатое представление необработанных данных. Векторы полезны в уменьшении размерности; вектор сжимает необработанные данные в меньшее количество существенных измерений. Автоэнкодеры соединены с декодерами, что позволяет реконструировать входные данные на основе их скрытого представления.

RBM — это математический эквивалент двустороннего переводчика. Прямой проход принимает входные данные и переводит их в набор чисел, который кодирует входные данные. Обратный проход тем временем берет этот набор чисел и переводит их обратно в восстановленные входные данные. Хорошо обученная сеть выполняет подпорку с высокой степенью точности.

На обоих этапах вес и смещения играют критическую роль; они помогают RBM в декодировании взаимосвязей между входами и в определении того, какие входы важны для обнаружения шаблонов. Посредством прямого и обратного проходов RBM обучается восстанавливать входные данные с различными весами и смещениями до тех пор, пока входные данные и конструкция там не станут как можно ближе. Интересным аспектом RBM является то, что данные не должны быть помечены. Это оказывается очень важным для наборов данных реального мира, таких как фотографии, видео, голоса и данные датчиков, которые, как правило, не имеют маркировки. Вместо ручной маркировки данных людьми, RBM автоматически сортирует данные; путем правильной настройки весов и смещений, RBM может извлечь важные функции и реконструировать входные данные. RBM является частью семейства нейронных сетей экстракторов признаков, которые предназначены для распознавания присущих им данных в данных. Они также называются авто-кодерами, потому что они должны кодировать свою собственную структуру.

Сети глубокого убеждения — DBNs

Сети глубокого убеждения (DBN) формируются путем объединения RBM и внедрения умного метода обучения. У нас есть новая модель, которая окончательно решает проблему исчезающего градиента. Джефф Хинтон изобрел RBM, а также сети Deep Belief как альтернативу обратному распространению.

DBN похожа по структуре на MLP (многослойный персептрон), но очень отличается, когда дело доходит до обучения. это обучение, которое позволяет DBNs превзойти своих мелких коллег

DBN может быть визуализирован как стек RBM, где скрытый уровень одного RBM является видимым уровнем RBM над ним. Первый RBM обучен, чтобы реконструировать свой вклад как можно точнее.

Скрытый уровень первого RBM берется в качестве видимого уровня второго RBM, и второй RBM обучается с использованием выходных данных первого RBM. Этот процесс повторяется до тех пор, пока каждый слой в сети не будет обучен.

В DBN каждый RBM изучает весь ввод. DBN работает глобально, точно настраивая весь вход последовательно, поскольку модель медленно улучшается, как объектив камеры, медленно фокусирующий изображение. Стек RBM превосходит один RBM, так как многослойный персептрон MLP превосходит один персептрон.

На этом этапе RBM обнаружили характерные шаблоны в данных, но без каких-либо имен или меток. Чтобы завершить обучение DBN, мы должны ввести метки в шаблоны и настроить сеть с помощью контролируемого обучения.

Нам нужен очень маленький набор помеченных образцов, чтобы функции и шаблоны могли быть связаны с именем. Этот небольшой набор данных используется для обучения. Этот набор помеченных данных может быть очень маленьким по сравнению с исходным набором данных.

Веса и смещения слегка изменяются, что приводит к небольшому изменению восприятия сеткой шаблонов и часто к небольшому увеличению общей точности.

Обучение также может быть завершено за разумное время с использованием графических процессоров, дающих очень точные результаты по сравнению с мелкими сетями, и мы также видим решение проблемы исчезновения градиента.

Генеративные Состязательные Сети — ГАН

Генеративные противоборствующие сети — это глубокие нейронные сети, состоящие из двух сетей, расположенных друг против друга, таким образом, это «состязательное» название.

GAN были представлены в статье, опубликованной исследователями из Университета Монреаля в 2014 году. Эксперт по искусственному искусству Facebook Янн ЛеКан, ссылаясь на GAN, назвал состязательное обучение «самой интересной идеей за последние 10 лет в ML».

Потенциал GAN огромен, так как сканирование сети учится имитировать любое распределение данных. GAN можно научить создавать параллельные миры, поразительно похожие на наши, в любой области: изображения, музыка, речь, проза. Они в некотором роде художники-роботы, и их продукция впечатляет.

В GAN одна нейронная сеть, известная как генератор, генерирует новые экземпляры данных, а другая, дискриминатор, оценивает их на подлинность.

Допустим, мы пытаемся сгенерировать рукописные цифры, подобные найденным в наборе данных MNIST, который взят из реального мира. Работа дискриминатора, когда показан экземпляр из истинного набора данных MNIST, заключается в распознавании их как подлинных.

Теперь рассмотрим следующие шаги ГАН —

• Сеть генераторов принимает входные данные в виде случайных чисел и возвращает изображение.

• Это сгенерированное изображение передается в качестве входных данных в сеть дискриминатора вместе с потоком изображений, взятых из фактического набора данных.

• Дискриминатор принимает как реальные, так и поддельные изображения и возвращает вероятности, числа от 0 до 1, где 1 представляет прогноз подлинности, а 0 — поддельный.

• Таким образом, у вас есть двойной цикл обратной связи —

  • Дискриминатор находится в петле обратной связи с основополагающей правдой изображений, которые мы знаем.

  • Генератор находится в контуре обратной связи с дискриминатором.

Сеть генераторов принимает входные данные в виде случайных чисел и возвращает изображение.

Это сгенерированное изображение передается в качестве входных данных в сеть дискриминатора вместе с потоком изображений, взятых из фактического набора данных.

Дискриминатор принимает как реальные, так и поддельные изображения и возвращает вероятности, числа от 0 до 1, где 1 представляет прогноз подлинности, а 0 — поддельный.

Таким образом, у вас есть двойной цикл обратной связи —

Дискриминатор находится в петле обратной связи с основополагающей правдой изображений, которые мы знаем.

Генератор находится в контуре обратной связи с дискриминатором.

Рекуррентные нейронные сети — RNNs

RNN Саре нейронных сетей, в которых данные могут передаваться в любом направлении. Эти сети используются для таких приложений, как моделирование языка или обработка естественного языка (NLP).

Основная концепция, лежащая в основе RNN, заключается в использовании последовательной информации. В нормальной нейронной сети предполагается, что все входы и выходы независимы друг от друга. Если мы хотим предсказать следующее слово в предложении, мы должны знать, какие слова предшествовали ему.

RNN называются рекуррентными, поскольку они повторяют одну и ту же задачу для каждого элемента последовательности, причем выходные данные основаны на предыдущих вычислениях. Таким образом, можно сказать, что RNN имеют «память», которая захватывает информацию о том, что было вычислено ранее. Теоретически, RNN могут использовать информацию в очень длинных последовательностях, но в действительности они могут оглянуться назад лишь на несколько шагов.

Сети с кратковременной памятью (LSTM) являются наиболее часто используемыми сетями RNN.

Вместе с сверточными нейронными сетями RNN использовались как часть модели для создания описаний немаркированных изображений. Удивительно, насколько хорошо это работает.

Сверточные глубокие нейронные сети — CNNs

Если мы увеличиваем количество слоев в нейронной сети, чтобы сделать ее глубже, это увеличивает сложность сети и позволяет нам моделировать более сложные функции. Однако количество весов и уклонов будет экспоненциально увеличиваться. На самом деле, изучение таких сложных проблем может стать невозможным для обычных нейронных сетей. Это приводит к решению, сверточные нейронные сети.

CNN широко используются в компьютерном зрении; были применены также в акустическом моделировании для автоматического распознавания речи.

Идея, лежащая в основе сверточных нейронных сетей, заключается в идее «движущегося фильтра», который проходит через изображение. Этот движущийся фильтр, или свертка, применяется к определенной окрестности узлов, которые, например, могут быть пикселями, где примененный фильтр равен 0,5 x значению узла —

Известный исследователь Янн ЛеКан был пионером сверточных нейронных сетей. Facebook как программное обеспечение для распознавания лиц использует эти сети. CNN был идеальным решением для проектов машинного зрения. Существует много слоев в сверточной сети. В конкурсе Imagenet в 2015 году машина смогла победить человека при распознавании объекта.

Короче говоря, сверточные нейронные сети (CNN) являются многослойными нейронными сетями. Слои иногда до 17 или более и предполагают, что входными данными являются изображения.

CNN резко сокращают количество параметров, которые необходимо настроить. Таким образом, CNN эффективно справляются с высокой размерностью необработанных изображений.

Python Deep Learning — Основы

В этой главе мы рассмотрим основы глубокого обучения Python.

Модели / алгоритмы глубокого обучения

Давайте теперь узнаем о различных моделях / алгоритмах глубокого обучения.

Вот некоторые из популярных моделей глубокого обучения:

• Сверточные нейронные сети
• Рекуррентные нейронные сети
• Глубокие сети убеждений
• Генеративные состязательные сети
• Авто-кодировщики и т. Д.

Входы и выходы представлены в виде векторов или тензоров. Например, нейронная сеть может иметь входы, где отдельные пиксельные значения RGB в изображении представлены как векторы.

Слои нейронов, которые лежат между входным слоем и выходным слоем, называются скрытыми слоями. Именно здесь большая часть работы происходит, когда нейронная сеть пытается решить проблемы. Если присмотреться к скрытым слоям, можно многое узнать о функциях, которые сеть научилась извлекать из данных.

Различные архитектуры нейронных сетей формируются путем выбора, какие нейроны подключаться к другим нейронам в следующем слое.

Псевдокод для расчета выхода

Ниже приведен псевдокод для расчета выходного сигнала распространяющейся вперед нейронной сети.

• # node []: = массив топологически отсортированных узлов
• # Ребро от a до b означает a слева от b
• # Если нейронная сеть имеет R входов и S выходов,
• # тогда первые R узлы являются входными узлами, а последние S узлы являются выходными узлами.
• # входящие [x]: = узлы, связанные с узлом x
• # weight [x]: = веса входящих ребер в x

Для каждого нейрона х слева направо —

• если x <= R: ничего не делать # это входной узел
• входы [x] = [output [i] для i во входящем [x]]
• weighted_sum = dot_product (weights [x], входные данные [x])
• output [x] = Activation_function (weighted_sum)

Обучение нейронной сети

Теперь мы научимся обучать нейронную сеть. Мы также изучим алгоритм обратного распространения и обратный проход в Python Deep Learning.

Мы должны найти оптимальные значения весов нейронной сети, чтобы получить желаемый результат. Для обучения нейронной сети мы используем метод итеративного градиентного спуска. Начнем сначала со случайной инициализации весов. После случайной инициализации мы делаем прогнозы для некоторого подмножества данных с помощью процесса прямого распространения, вычисляем соответствующую функцию стоимости C и обновляем каждый вес w на величину, пропорциональную dC / dw, т. Е. Производной от функций стоимости по вес. Константа пропорциональности известна как скорость обучения.

Градиенты могут быть эффективно рассчитаны с использованием алгоритма обратного распространения. Ключевое наблюдение обратного распространения или обратной поддержки состоит в том, что из-за цепного правила дифференцировки градиент у каждого нейрона в нейронной сети может быть рассчитан с использованием градиента у нейронов, к которым он имеет исходящие ребра. Следовательно, мы рассчитываем градиенты в обратном направлении, то есть сначала вычисляем градиенты выходного слоя, затем самый верхний скрытый слой, затем предшествующий скрытый слой и т. Д., Заканчивающиеся на входном слое.

Алгоритм обратного распространения реализуется в основном с использованием идеи вычислительного графа, где каждый нейрон расширяется до множества узлов в вычислительном графе и выполняет простую математическую операцию, такую ​​как сложение, умножение. Вычислительный граф не имеет весов на ребрах; все веса присваиваются узлам, поэтому веса становятся их собственными узлами. Затем алгоритм обратного распространения запускается на вычислительном графе. Как только вычисление завершено, для обновления требуются только градиенты весовых узлов. Остальные градиенты могут быть отброшены.

Метод оптимизации градиентного спуска

Одна из часто используемых функций оптимизации, которая корректирует веса в соответствии с вызванной ими ошибкой, называется «градиентным спуском».

Градиент — это другое название уклона, а уклон на графике xy показывает, как две переменные связаны друг с другом: подъем по трассе, изменение расстояния по изменению во времени и т. Д. В этом случае наклон соотношение между ошибкой сети и одним весом; то есть, как ошибка изменяется при изменении веса.

Точнее сказать, мы хотим выяснить, какой вес дает наименьшую ошибку. Мы хотим найти вес, который правильно представляет сигналы, содержащиеся во входных данных, и переводит их в правильную классификацию.

По мере того как нейронная сеть учится, она медленно корректирует многие веса, чтобы они могли правильно отображать значение сигнала. Соотношение между Сетевой ошибкой и каждым из этих весовых коэффициентов является производной, dE / dw, которая вычисляет степень, в которой небольшое изменение веса вызывает небольшое изменение ошибки.

Каждый вес является лишь одним фактором в глубокой сети, которая включает в себя множество преобразований; Сигнал веса проходит через активации и суммируется по нескольким слоям, поэтому мы используем цепное правило исчисления для обратной работы по активациям и выходам сети. Это приводит нас к рассматриваемому весу и его связи с общей ошибкой.

Данные две переменные, ошибка и вес, опосредованы третьей переменной, активацией , через которую передается вес. Мы можем рассчитать, как изменение веса влияет на изменение ошибки, сначала рассчитав, как изменение активации влияет на изменение ошибки, и как изменение веса влияет на изменение активации.

Основная идея глубокого обучения — это не более чем: корректировка весов модели в ответ на ошибку, которую она производит, до тех пор, пока вы больше не сможете уменьшить ошибку.

Глубокая сеть обучается медленно, если значение градиента мало, и быстро, если значение велико. Любые неточности в обучении приводят к неточным результатам. Процесс обучения сетей от выхода до входа называется обратным распространением или обратным ходом. Мы знаем, что прямое распространение начинается с ввода и работает вперед. Back prop выполняет обратный / обратный расчет градиента справа налево.

Каждый раз, когда мы вычисляем градиент, мы используем все предыдущие градиенты до этой точки.

Давайте начнем с узла в выходном слое. Край использует градиент в этом узле. Когда мы возвращаемся в скрытые слои, это становится все более сложным. Произведение двух чисел от 0 до 1 дает вам меньшее число. Значение градиента продолжает уменьшаться, и в результате обратная тренировка занимает много времени, и точность снижается.

Проблемы в алгоритмах глубокого обучения

Существуют определенные проблемы как для мелких нейронных сетей, так и для глубоких нейронных сетей, такие как переоснащение и время вычислений. На DNN влияет переоснащение, потому что используются дополнительные уровни абстракции, которые позволяют им моделировать редкие зависимости в обучающих данных.

Методы регуляризации, такие как выбывание, ранняя остановка, увеличение данных, трансферное обучение, применяются во время тренировок для борьбы с переоснащением. Выпадающая регуляризация случайно пропускает юниты из скрытых слоев во время обучения, что помогает избежать редких зависимостей. DNN учитывают несколько параметров обучения, таких как размер, то есть количество слоев и количество единиц на слой, скорость обучения и начальные веса. Поиск оптимальных параметров не всегда практичен из-за высокой стоимости времени и вычислительных ресурсов. Несколько хаков, таких как пакетная обработка, могут ускорить вычисления. Большая вычислительная мощность графических процессоров значительно помогла процессу обучения, поскольку требуемые матричные и векторные вычисления хорошо выполняются на графических процессорах.

Выбывать

Dropout — популярный метод регуляризации для нейронных сетей. Глубокие нейронные сети особенно подвержены переобучению.

Давайте теперь посмотрим, что такое отсев и как он работает.

По словам Джеффри Хинтона, одного из пионеров Deep Learning: «Если у вас есть глубокая нейронная сеть и она не переоснащается, вам, вероятно, следует использовать более крупную и использовать dropout».

Удаление — это метод, при котором во время каждой итерации градиентного спуска мы отбрасываем набор случайно выбранных узлов. Это означает, что мы игнорируем некоторые узлы случайным образом, как будто они не существуют.

Каждый нейрон хранится с вероятностью q и случайно падает с вероятностью 1-q. Значение q может быть различным для каждого слоя в нейронной сети. Значение 0,5 для скрытых слоев и 0 для входного слоя хорошо подходит для широкого круга задач.

Во время оценки и прогноза отсев не используется. Выход каждого нейрона умножается на q, так что вход на следующий слой имеет то же ожидаемое значение.

Идея Dropout заключается в следующем: в нейронной сети без регуляризации отсева нейроны развивают взаимозависимость друг с другом, что приводит к переоснащению.

Хитрость реализации

Выпадение реализовано в библиотеках, таких как TensorFlow и Pytorch, сохраняя выходные данные случайно выбранных нейронов равными 0. То есть, хотя нейрон существует, его выходные данные перезаписываются как 0.

Ранняя остановка

Мы обучаем нейронные сети, используя итерационный алгоритм, называемый градиентным спуском.

Идея ранней остановки интуитивна; мы прекращаем обучение, когда ошибка начинает увеличиваться. Здесь под ошибкой мы подразумеваем ошибку, измеренную в проверочных данных, которая является частью обучающих данных, используемых для настройки гиперпараметров. В этом случае гиперпараметр является критерием остановки.

Увеличение данных

Процесс, в котором мы увеличиваем количество имеющихся у нас данных или увеличиваем их, используя существующие данные и применяя к ним некоторые преобразования. Точные используемые преобразования зависят от задачи, которую мы намерены достичь. Более того, преобразования, которые помогают нейронной сети, зависят от ее архитектуры.

Например, во многих задачах компьютерного зрения, таких как классификация объектов, эффективный метод увеличения данных — это добавление новых точек данных, которые являются обрезанными или переведенными версиями исходных данных.

Когда компьютер принимает изображение в качестве входных данных, он принимает массив значений пикселей. Допустим, что все изображение смещено влево на 15 пикселей. Мы применяем много разных сдвигов в разных направлениях, в результате чего расширенный набор данных во много раз превосходит исходный набор данных.

Передача обучения

Процесс взятия предварительно обученной модели и «точной настройки» модели с нашим собственным набором данных называется трансферным обучением. Есть несколько способов сделать это. Несколько способов описаны ниже —

• Мы обучаем предварительно обученную модель на большом наборе данных. Затем мы удаляем последний слой сети и заменяем его новым слоем со случайными весами.

• Затем мы замораживаем веса всех других слоев и обучаем сеть в обычном режиме. Здесь замораживание слоев не меняет вес во время градиентного спуска или оптимизации.

Мы обучаем предварительно обученную модель на большом наборе данных. Затем мы удаляем последний слой сети и заменяем его новым слоем со случайными весами.

Затем мы замораживаем веса всех других слоев и обучаем сеть в обычном режиме. Здесь замораживание слоев не меняет вес во время градиентного спуска или оптимизации.

Концепция этого заключается в том, что предварительно обученная модель будет действовать как экстрактор признаков, и только последний уровень будет обучен текущей задаче.

Вычислительные графики

Обратное распространение реализуется в средах глубокого обучения, таких как Tensorflow, Torch, Theano и т. Д., С использованием вычислительных графов. Что еще более важно, понимание обратного распространения на вычислительных графах сочетает в себе несколько различных алгоритмов и их вариаций, таких как backprop по времени и backprop с общими весами. Как только все преобразуется в вычислительный граф, они остаются тем же алгоритмом — просто обратное распространение на вычислительных графах.

Что такое вычислительный граф

Вычислительный граф определяется как ориентированный граф, где узлы соответствуют математическим операциям. Вычислительные графики — это способ выражения и оценки математического выражения.

Например, вот простое математическое уравнение —

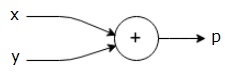
$$p = x + y$$

Мы можем нарисовать расчетный график вышеприведенного уравнения следующим образом.

Вышеупомянутый вычислительный граф имеет узел сложения (узел со знаком «+») с двумя входными переменными x и y и одним выходным q.

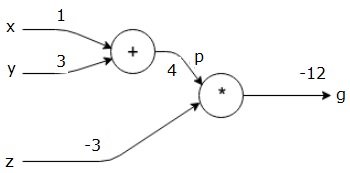
Давайте возьмем другой пример, немного более сложный. У нас есть следующее уравнение.

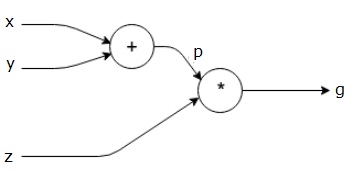
$$g = \ left (x + y \ right) \ ast z$$

Вышеупомянутое уравнение представлено следующим вычислительным графиком.

Вычислительные графики и обратное распространение

Вычислительные графики и обратное распространение, оба являются важными основными понятиями в глубоком обучении для обучения нейронных сетей.

Форвард Пасс

Прямой проход — это процедура оценки значения математического выражения, представленного вычислительными графами. Выполнение прямого прохода означает, что мы передаем значение из переменных в прямом направлении слева (вход) вправо, где вывод.

Давайте рассмотрим пример, дав некоторую ценность всем входам. Предположим, следующие значения даны для всех входов.

$$x = 1, y = 3, z = −3$$

Передавая эти значения на входы, мы можем выполнить прямой переход и получить следующие значения для выходов на каждом узле.

Сначала мы используем значения x = 1 и y = 3, чтобы получить p = 4.

Затем мы используем p = 4 и z = -3, чтобы получить g = -12. Идем слева направо, вперед.

Цели обратного прохода

В обратном проходе наше намерение состоит в том, чтобы вычислить градиенты для каждого входа относительно конечного результата. Эти градиенты необходимы для обучения нейронной сети с использованием градиентного спуска.

Например, мы хотим следующие градиенты.

Желаемые градиенты

$$\ frac {\ частичный х} {\ частичный ф}, \ frac {\ частичный у} {\ частичный ф}, \ frac {\ частичный г} {\ частичный ф}$$

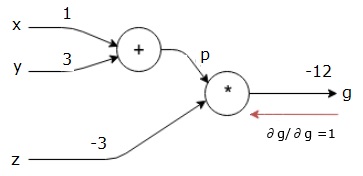
Обратный проход (обратное распространение)

Мы начинаем обратный проход, находя производную конечного результата по конечному результату (самому!). Таким образом, это приведет к выводу идентичности, и значение будет равно единице.

$$\ frac {\ частичный г} {\ частичный г} = 1$$

Наш вычислительный график теперь выглядит так, как показано ниже —

Далее мы сделаем обратный проход через операцию «*». Мы рассчитаем градиенты в точках p и z. Поскольку g = p * z, мы знаем, что —

$$\ frac {\ частичный г} {\ частичный г} = p$$

$$\ frac {\ частичный г} {\ частный р} = z$$

Мы уже знаем значения z и p из прямого прохода. Следовательно, мы получаем —

$$\ frac {\ частичный г} {\ частичный г} = p = 4$$

а также

$$\ frac {\ частичный г} {\ частичный р} = z = -3$$

Мы хотим рассчитать градиенты в х и у —

$$\ frac {\ частичный г} {\ частичный х}, \ frac {\ частичный г} {\ частичный г}$$

Однако мы хотим сделать это эффективно (хотя x и g на этом графике находятся всего в двух шагах, представьте, что они действительно далеки друг от друга). Чтобы эффективно рассчитать эти значения, мы будем использовать цепное правило дифференцирования. Из правила цепочки имеем:

$$\ frac {\ частичный г} {\ частичный х} = \ фрак {\ частичный г} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный х}$$

$$\ frac {\ частичный г} {\ частичный y} = \ frac {\ частичный г} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный у}$$

Но мы уже знаем, что dg / dp = -3, dp / dx и dp / dy просты, так как p напрямую зависит от x и y. У нас есть —

$$p = x + y \ Rightarrow \ frac {\ частичный x} {\ частичный p} = 1, \ frac {\ частичный y} {\ частичный p} = 1$$

Следовательно, мы получаем —

$$\ frac {\ частичный г} {\ частичный ф} = \ частичный {} частичный г} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный х} = \ левый (-3 \ правый) .1 = -3$$

Кроме того, для ввода у —

$$\ frac {\ частичный г} {\ частичный у} = \ частичный {} частичный} {\ частичный р} \ ast \ frac {\ частичный р} {\ частичный у} = \ левый (-3 \ правый) .1 = -3$$

Основная причина сделать это в обратном направлении заключается в том, что когда нам нужно было вычислить градиент в точке x, мы использовали только уже вычисленные значения и dq / dx (производная от вывода узла по отношению к входу того же узла). Мы использовали локальную информацию для вычисления глобального значения.

Шаги для обучения нейронной сети

Выполните следующие шаги для обучения нейронной сети —

• Для точки данных x в наборе данных мы передаем передачу с x в качестве входных данных и рассчитаем стоимость c в качестве выходных данных.

• Мы делаем обратный проход, начиная с c, и вычисляем градиенты для всех узлов в графе. Это включает в себя узлы, которые представляют веса нейронной сети.

• Затем мы обновляем вес, выполняя W = W — скорость обучения * градиенты.

• Мы повторяем этот процесс, пока не будут выполнены критерии остановки.

Для точки данных x в наборе данных мы передаем передачу с x в качестве входных данных и рассчитаем стоимость c в качестве выходных данных.

Мы делаем обратный проход, начиная с c, и вычисляем градиенты для всех узлов в графе. Это включает в себя узлы, которые представляют веса нейронной сети.

Затем мы обновляем вес, выполняя W = W — скорость обучения * градиенты.

Мы повторяем этот процесс, пока не будут выполнены критерии остановки.

Python Deep Learning — Приложения

Глубокое обучение дало хорошие результаты для нескольких приложений, таких как компьютерное зрение, языковой перевод, субтитры, аудио-транскрипция, молекулярная биология, распознавание речи, обработка естественного языка, автомобили с автоматическим управлением, обнаружение опухоли мозга, перевод речи в реальном времени, музыка состав, автоматическая игра и тд.

Глубокое обучение — это следующий большой шаг после машинного обучения с более продвинутой реализацией. В настоящее время он движется к тому, чтобы стать отраслевым стандартом, приносящим большие надежды на то, чтобы изменить игру при работе с необработанными неструктурированными данными.

Глубокое обучение в настоящее время является одним из лучших поставщиков решений для широкого спектра реальных проблем. Разработчики создают программы ИИ, которые вместо использования ранее заданных правил учатся на примерах для решения сложных задач. С глубоким обучением, используемым многими исследователями данных, более глубокие нейронные сети обеспечивают результаты, которые становятся все более точными.

Идея состоит в том, чтобы разработать глубокие нейронные сети путем увеличения количества уровней обучения для каждой сети; Машина узнает больше о данных, пока они не станут максимально точными. Разработчики могут использовать методы глубокого обучения для реализации сложных задач машинного обучения и обучать сети искусственного интеллекта иметь высокий уровень восприятия восприятия.

Глубокое обучение находит свою популярность в компьютерном зрении. Здесь одной из решаемых задач является классификация изображений, где заданные входные изображения классифицируются как кошка, собака и т. Д. Или как класс или метка, которая наилучшим образом описывает изображение. Мы, люди, учимся тому, как выполнять эту задачу в самом начале нашей жизни, и обладаем навыками быстрого распознавания шаблонов, обобщения из предшествующих знаний и адаптации к различным изображениям.

Библиотеки и рамки

В этой главе мы будем связывать глубокое обучение с различными библиотеками и структурами.

Глубокое обучение и Теано

Если мы хотим начать кодирование глубокой нейронной сети, лучше у нас будет представление о том, как работают различные фреймворки, такие как Theano, TensorFlow, Keras, PyTorch и т. Д.

Theano — это библиотека Python, которая предоставляет набор функций для построения глубоких сетей, которые быстро обучаются на нашей машине.

Theano был разработан в Университете Монреаля, Канада, под руководством Йошуа Бенжио, пионера сети.

Theano позволяет нам определять и оценивать математические выражения с помощью векторов и матриц, которые представляют собой прямоугольные массивы чисел.

Технически говоря, как нейронные сети, так и входные данные могут быть представлены в виде матриц, а все стандартные сетевые операции могут быть переопределены как матричные операции. Это важно, поскольку компьютеры могут выполнять матричные операции очень быстро.

Мы можем обрабатывать несколько значений матрицы параллельно, и если мы построим нейронную сеть с этой базовой структурой, мы можем использовать одну машину с графическим процессором для обучения огромных сетей за разумное время.

Однако, если мы используем Theano, мы должны построить глубокую сеть с нуля. Библиотека не предоставляет полной функциональности для создания определенного типа глубокой сети.

Вместо этого мы должны кодировать каждый аспект глубокой сети, такой как модель, слои, активация, метод обучения и любые специальные методы, чтобы прекратить переоснащение.

Хорошая новость заключается в том, что Theano позволяет строить нашу реализацию поверх векторизованных функций, предоставляя нам высоко оптимизированное решение.

Есть много других библиотек, которые расширяют функциональность Theano. TensorFlow и Keras можно использовать с Theano в качестве бэкэнда.

Глубокое обучение с TensorFlow

Googles TensorFlow — это библиотека питонов. Эта библиотека — отличный выбор для создания приложений глубокого обучения коммерческого уровня.

TensorFlow вырос из другой библиотеки DistBelief V2, которая была частью Google Brain Project. Эта библиотека призвана расширить мобильность машинного обучения, чтобы исследовательские модели могли применяться к приложениям коммерческого уровня.

Подобно библиотеке Theano, TensorFlow основан на вычислительных графах, где узел представляет постоянные данные или математическую операцию, а ребра представляют поток данных между узлами, который представляет собой многомерный массив или тензор; отсюда и название TensorFlow

Выход из операции или набора операций подается как вход в следующую.

Несмотря на то, что TensorFlow был разработан для нейронных сетей, он хорошо работает для других сетей, где вычисления могут быть смоделированы как граф потока данных.

TensorFlow также использует несколько функций из Theano, таких как устранение общих и подвыражений, автоматическое дифференцирование, общие и символические переменные.

Различные типы глубоких сетей могут быть построены с использованием TensorFlow, таких как сверточные сети, автоэнкодеры, RNTN, RNN, RBM, DBM / MLP и так далее.

Однако в TensorFlow отсутствует поддержка настройки гиперпараметров. Для этой функции мы можем использовать Keras.

Глубокое обучение и керас

Keras — это мощная и простая в использовании библиотека Python для разработки и оценки моделей глубокого обучения.

Он имеет минималистский дизайн, который позволяет нам создавать сеть слой за слоем; тренируй и беги.

Он объединяет эффективные библиотеки численных вычислений Theano и TensorFlow и позволяет нам определять и обучать модели нейронных сетей в несколько коротких строк кода.

Это высокоуровневый API нейронной сети, помогающий широко использовать глубокое обучение и искусственный интеллект. Он работает поверх ряда библиотек более низкого уровня, включая TensorFlow, Theano и так далее. Код Keras является переносимым; мы можем реализовать нейронную сеть в Keras, используя Theano или TensorFlow в качестве бэк-энда без каких-либо изменений в коде.

Python Deep Learning — Внедрения

В этой реализации глубокого обучения наша цель состоит в том, чтобы предсказать потери клиентов или данные о сбое определенного банка — какие клиенты, вероятно, покинут эту банковскую услугу. Используемый набор данных является относительно небольшим и содержит 10000 строк с 14 столбцами. Мы используем дистрибутив Anaconda и такие фреймворки, как Theano, TensorFlow и Keras. Keras построен поверх Tensorflow и Theano, которые функционируют как его бэкэнды.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Шаг 1: Предварительная обработка данных

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Шаг 2

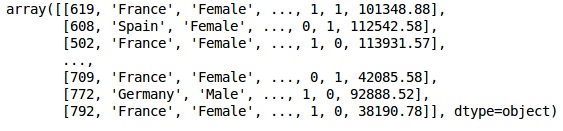
Мы создаем матрицы объектов набора данных и целевой переменной, которая является столбцом 14 и помечена как «Exited».

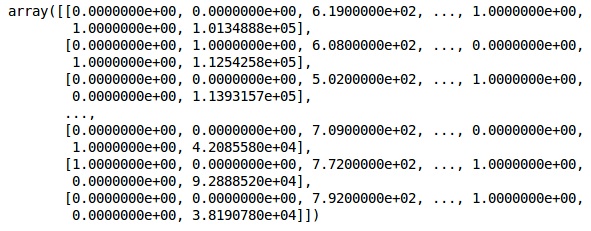
Первоначальный вид данных, как показано ниже —

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Выход

Шаг 3

Y

Выход

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Шаг 4

Мы делаем анализ проще, кодируя строковые переменные. Мы используем функцию ScikitLearn LabelEncoder для автоматического кодирования различных меток в столбцах со значениями от 0 до n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Выход

В приведенном выше выводе названия стран заменяются на 0, 1 и 2; в то время как мужчины и женщины заменены на 0 и 1.

Шаг 5

Маркировка закодированных данных

Мы используем ту же библиотеку ScikitLearn и другую функцию под названием OneHotEncoder, чтобы просто передать номер столбца, создавая фиктивную переменную.

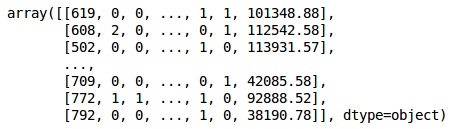
onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Теперь первые 2 столбца представляют страну, а 4-й столбец представляет пол.

Выход

Мы всегда делим наши данные на части обучения и тестирования; мы обучаем нашу модель на данных обучения, а затем проверяем точность модели на данных тестирования, которая помогает оценить эффективность модели.

Шаг 6

Мы используем функцию train_test_split ScikitLearn для разделения наших данных на тренировочный набор и тестовый набор. Мы сохраняем соотношение между поездом и тестом как 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Некоторые переменные имеют значения в тысячах, а некоторые имеют значения в десятках или единицах. Мы масштабируем данные так, чтобы они были более представительными.

Шаг 7

В этом коде мы подгоняем и трансформируем тренировочные данные, используя функцию StandardScaler . Мы стандартизируем наше масштабирование так, чтобы мы использовали тот же самый подобранный метод для преобразования / масштабирования тестовых данных.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

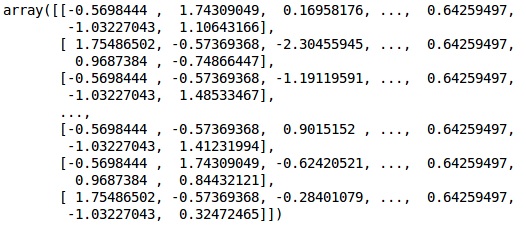
Выход

Данные теперь масштабируются правильно. Наконец, мы закончили с предварительной обработкой данных. Теперь мы начнем с нашей модели.

Шаг 8

Мы импортируем необходимые модули здесь. Нам нужен последовательный модуль для инициализации нейронной сети и плотный модуль для добавления скрытых слоев.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Шаг 9

Мы назовем модель классификатором, поскольку наша цель — классифицировать отток клиентов. Затем мы используем последовательный модуль для инициализации.

#Initializing Neural Network 
classifier = Sequential()

Шаг 10

Мы добавляем скрытые слои один за другим, используя плотную функцию. В приведенном ниже коде мы увидим много аргументов.

Наш первый параметр — output_dim . Это количество узлов, которые мы добавляем в этот слой. init — это инициализация стохастического градиента. В нейронной сети мы присваиваем веса каждому узлу. При инициализации веса должны быть близки к нулю, и мы случайным образом инициализируем веса, используя равномерную функцию. Параметр input_dim необходим только для первого слоя, так как модель не знает количество наших входных переменных. Здесь общее количество входных переменных равно 11. Во втором слое модель автоматически знает количество входных переменных из первого скрытого слоя.

Выполните следующую строку кода, чтобы добавить входной слой и первый скрытый слой —

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Выполните следующую строку кода, чтобы добавить второй скрытый слой —

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Выполните следующую строку кода, чтобы добавить выходной слой —

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Шаг 11

Компиляция ANN

Мы добавили несколько слоев в наш классификатор до сих пор. Теперь мы скомпилируем их, используя метод compile . Аргументы, добавленные в окончательный контроль компиляции, завершают работу нейронной сети. Итак, нам нужно быть осторожным на этом этапе.

Вот краткое объяснение аргументов.

Первый аргумент — Оптимизатор. Это алгоритм, используемый для поиска оптимального набора весов. Этот алгоритм называется стохастическим градиентным спуском (SGD) . Здесь мы используем один из нескольких типов, называемый «оптимизатором Адама». SGD зависит от потерь, поэтому наш второй параметр — потери. Если наша зависимая переменная является двоичной, мы используем функцию логарифмической потери, называемую «binary_crossentropy» , и если наша зависимая переменная имеет более двух категорий в выводе, то мы используем «categoryorical_crossentropy» . Мы хотим улучшить производительность нашей нейронной сети на основе точности , поэтому мы добавляем метрики в качестве точности.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Шаг 12

На этом этапе необходимо выполнить несколько кодов.

Установка ANN в тренировочный набор

Теперь мы обучаем нашу модель на тренировочных данных. Мы используем метод подгонки, чтобы соответствовать нашей модели. Мы также оптимизируем веса для повышения эффективности моделей. Для этого мы должны обновить веса. Размер партии — это число наблюдений, после которого мы обновляем весы. Epoch — общее количество итераций. Значения размера партии и эпохи выбираются методом проб и ошибок.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Делать прогнозы и оценивать модель

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Прогнозирование одного нового наблюдения

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Шаг 13

Прогнозирование результата теста

Результат прогноза даст вам вероятность того, что клиент покинет компанию. Мы преобразуем эту вероятность в двоичные 0 и 1.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Шаг 14

Это последний шаг, где мы оцениваем производительность нашей модели. У нас уже есть оригинальные результаты, и, таким образом, мы можем построить путаницу для проверки точности нашей модели.

Создание матрицы путаницы

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Выход

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

Из матрицы путаницы, точность нашей модели может быть рассчитана как —

Accuracy = 1541+175/2000=0.858

Мы достигли 85,8% точности , что хорошо.

Алгоритм прямого распространения

В этом разделе мы узнаем, как написать код для прямого распространения (прогнозирования) для простой нейронной сети —

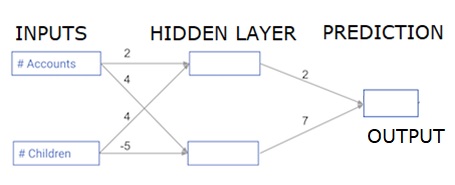
Каждая точка данных является клиентом. Первый вход — сколько у них учетных записей, а второй — сколько у них детей. Модель будет прогнозировать, сколько транзакций совершит пользователь в следующем году.

Входные данные предварительно загружаются в качестве входных данных, а весовые коэффициенты находятся в словаре, называемом весовыми коэффициентами. Массив весов для первого узла в скрытом слое указывается в весах [‘node_0’], а для второго узла в скрытом слое — в весах [‘node_1’] соответственно.

Веса, подающие в выходной узел, доступны в весах.

Выпрямленная функция линейной активации

«Функция активации» — это функция, которая работает на каждом узле. Это преобразовывает вход узла в некоторый вывод.

Выпрямленная функция линейной активации (называемая ReLU ) широко используется в очень высокопроизводительных сетях. Эта функция принимает одно число как вход, возвращая 0, если вход отрицательный, и ввод как выход, если вход положительный.

Вот несколько примеров —

• relu (4) = 4
• relu (-2) = 0

Заполним определение функции relu () —

• Мы используем функцию max (), чтобы вычислить значение для вывода relu ().
• Мы применяем функцию relu () к node_0_input для вычисления node_0_output.
• Мы применяем функцию relu () к node_1_input для вычисления node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Выход

0.9950547536867305
-3

Применение сети ко многим наблюдениям / рядам данных

В этом разделе мы узнаем, как определить функцию под названиемgnast_With_Network (). Эта функция будет генерировать прогнозы для нескольких наблюдений данных, взятых из сети выше, взятой как input_data. Веса, указанные в приведенной выше сети, используются. Определение функции relu () также используется.

Давайте определим функцию под названиемgnestt_with_network (), которая принимает два аргумента — input_data_row и weights — и возвращает прогноз из сети в качестве вывода.

Мы вычисляем входные и выходные значения для каждого узла, сохраняя их как: node_0_input, node_0_output, node_1_input и node_1_output.

Чтобы вычислить входное значение узла, мы умножаем соответствующие массивы вместе и вычисляем их сумму.

Чтобы вычислить выходное значение узла, мы применяем функцию relu () к входному значению узла. Мы используем цикл for для перебора входных данных —

Мы также используем нашу Предикат_with_network () для генерации прогнозов для каждой строки input_data — input_data_row. Мы также добавляем каждый прогноз к результатам.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Выход

[0, 12]

Здесь мы использовали функцию relu, где relu (26) = 26 и relu (-13) = 0 и так далее.

Глубокие многослойные нейронные сети

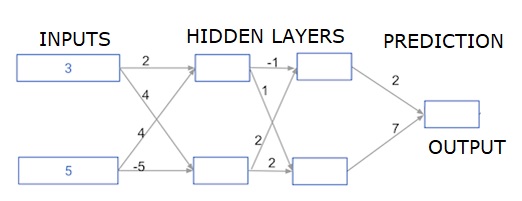
Здесь мы пишем код для прямого распространения для нейронной сети с двумя скрытыми слоями. Каждый скрытый слой имеет два узла. Входные данные были предварительно загружены как input_data . Узлы в первом скрытом слое называются node_0_0 и node_0_1.

Их веса предварительно загружены в виде весов [‘node_0_0’] и весов [‘node_0_1’] соответственно.

Узлы во втором скрытом слое называются node_1_0 и node_1_1 . Их веса предварительно загружены как веса [‘node_1_0’] и веса [‘node_1_1’] соответственно.

Затем мы создаем вывод модели из скрытых узлов, используя веса, предварительно загруженные в качестве весов [‘output’] .

Мы рассчитываем node_0_0_input с использованием его весовых весов [‘node_0_0’] и заданных input_data. Затем примените функцию relu (), чтобы получить node_0_0_output.

Мы делаем то же самое, что и выше для node_0_1_input, чтобы получить node_0_1_output.

Мы вычисляем node_1_0_input, используя его веса weights [‘node_1_0’] и выходные данные первого скрытого слоя — hidden_0_outputs. Затем мы применяем функцию relu () для получения node_1_0_output.

Мы делаем то же самое, что и выше для node_1_1_input, чтобы получить node_1_1_output.

Мы рассчитываем model_output, используя weights [‘output’] и выходные данные из второго скрытого массива hidden_1_outputs. Мы не применяем функцию relu () к этому выводу.