CSGraph расшифровывается как Compressed Sparse Graph , который фокусируется на алгоритмах Fast графа, основанных на разреженных матричных представлениях.
Графические представления
Для начала давайте разберемся, что такое разреженный граф и как он помогает в представлении графов.
Что такое разреженный граф?
Граф — это просто набор узлов, между которыми есть связи. Графики могут представлять почти все — соединения в социальных сетях, где каждый узел является личностью и связан со знакомыми; изображения, где каждый узел является пикселем и связан с соседними пикселями; точки в многомерном распределении, где каждый узел связан со своими ближайшими соседями и практически всем остальным, что вы можете себе представить.
Один очень эффективный способ представления данных графа — это разреженная матрица: назовем ее G. Матрица G имеет размер N x N, а G [i, j] дает значение связи между узлом «i» и узлом. ‘J’. Разреженный граф содержит в основном нули, то есть большинство узлов имеют только несколько соединений. Это свойство оказывается истинным в большинстве случаев, представляющих интерес.
Создание подмодуля разреженного графа было мотивировано несколькими алгоритмами, использованными в scikit-learn, которые включали следующее:
-
Isomap — алгоритм обучения многообразия, который требует нахождения кратчайших путей в графе.
-
Иерархическая кластеризация — алгоритм кластеризации, основанный на минимальном остовном дереве.
-
Спектральная декомпозиция — алгоритм проекции, основанный на лапласианах разреженных графов.
Isomap — алгоритм обучения многообразия, который требует нахождения кратчайших путей в графе.
Иерархическая кластеризация — алгоритм кластеризации, основанный на минимальном остовном дереве.
Спектральная декомпозиция — алгоритм проекции, основанный на лапласианах разреженных графов.
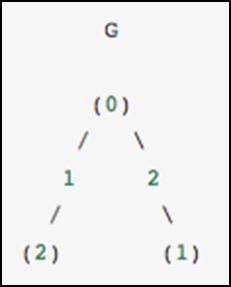
В качестве конкретного примера представьте, что мы хотели бы представить следующий неориентированный граф:
Этот граф имеет три узла, где узлы 0 и 1 соединены ребром веса 2, а узлы 0 и 2 соединены ребром веса 1. Мы можем построить плотные, замаскированные и разреженные представления, как показано в следующем примере. , имея в виду, что ненаправленный граф представлен симметричной матрицей.
G_dense = np.array([ [0, 2, 1], [2, 0, 0], [1, 0, 0] ]) G_masked = np.ma.masked_values(G_dense, 0) from scipy.sparse import csr_matrix G_sparse = csr_matrix(G_dense) print G_sparse.data
Вышеуказанная программа сгенерирует следующий вывод.
array([2, 1, 2, 1])
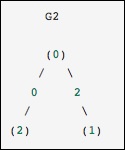
Это идентично предыдущему графику, за исключением того, что узлы 0 и 2 соединены ребром нулевого веса. В этом случае представленное выше плотное представление приводит к неоднозначности — как можно представить не-ребра, если ноль является значимым значением. В этом случае либо маскированное, либо разреженное представление должно использоваться для устранения неоднозначности.
Давайте рассмотрим следующий пример.
from scipy.sparse.csgraph import csgraph_from_dense G2_data = np.array ([ [np.inf, 2, 0 ], [2, np.inf, np.inf], [0, np.inf, np.inf] ]) G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf) print G2_sparse.data
Вышеуказанная программа сгенерирует следующий вывод.