В этом уроке мы имеем дело с проблемами, включающими выражения с 10 в качестве основания, имеющего отрицательные показатели.
Правила нахождения отрицательного показателя 10
Предположим, у нас есть выражение, имеющее 10 -n .
В нормальном курсе значение 10 -n находится путем умножения базы
10 ‘n’ раз в знаменателе и положить 1 в числителе.
Мы используем ярлык для решения такой проблемы. Мы смотрим на показатель степени, а затем записываем десятичную точку, за которой следует столько нулей, сколько на единицу меньше показателя степени и 1.
Оцените 10 -3
Шаг 1:
Здесь у нас есть выражение, включающее степень десяти с отрицательным показателем степени.
База равна 10, а показатель степени равен -3.
Шаг 2:
В обычном режиме значение 10 -3 можно найти, умножив основание 10 в знаменателе три раза и поставив 1 в числителе.
10 -3 = 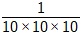
Шаг 3:
Используя ярлык, мы находим, что показатель степени равен -3. Мы записываем десятичную точку, за которой следуют два (1 меньше 3) нуля и 1.
Итак, 10 -3 = 0,001
Оцените 10 -5
Шаг 1:
Здесь у нас есть выражение, включающее степень десяти с отрицательным показателем степени.
База равна 10, а показатель степени равен -5.
Шаг 2:
В нормальном курсе значение 10 -5 находится путем умножения базового 10 на пять раз в знаменателе и ввода 1 в числитель.
10 -5 = 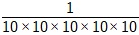
Шаг 3:
Используя ярлык, мы находим показатель степени -5. Мы записываем десятичную точку, за которой следуют четыре (1 меньше 5) нулей и 1.
Так 10 -5 = 0,00001