Что такое реляционная алгебра?
RELATIONAL ALGEBRA — широко используемый процедурный язык запросов. Он собирает экземпляры отношений в качестве входных данных и дает вхождения отношений в качестве выходных данных. Он использует различные операции для выполнения этого действия. Операции реляционной алгебры выполняются рекурсивно на отношении. Результатом этих операций является новое отношение, которое может быть сформировано из одного или нескольких входных отношений.
В этом уроке вы узнаете:
- Что такое реляционная алгебра?
- SELECT (σ)
- Проекция (π)
- Союз операция (у)
- Установить разницу (-)
- пересечение
- Декартово произведение (X)
- Присоединяйтесь Операции
- Внутреннее соединение:
- Тета
- EQUI присоединиться:
- ЕСТЕСТВЕННОЕ СОЕДИНЕНИЕ (⋈)
- НАРУЖНОЕ СОЕДИНЕНИЕ
- Левое внешнее соединение (A
B)
- Правое внешнее соединение: (A
B)
- Полное внешнее соединение: (A
B)
Основные операции по реляционной алгебре:
Relational Algebra devided in various groups
Unary Relational Operations
- SELECT (symbol: σ)
- PROJECT (symbol: π)
- RENAME (symbol: )
Relational Algebra Operations From Set Theory
- UNION (υ)
- INTERSECTION ( ),
- DIFFERENCE (-)
- CARTESIAN PRODUCT ( x )
Binary Relational Operations
- JOIN
- DIVISION
Let’s study them in detail:
SELECT (σ)
The SELECT operation is used for selecting a subset of the tuples according to a given selection condition. Sigma(σ)Symbol denotes it. It is used as an expression to choose tuples which meet the selection condition. Select operation selects tuples that satisfy a given predicate.
σp(r)
σ is the predicate
r stands for relation which is the name of the table
p is prepositional logic
Example 1
σ topic = "Database" (Tutorials)
Output — Selects tuples from Tutorials where topic = ‘Database’.
Example 2
σ topic = "Database" and author = "guru99"( Tutorials)
Output — Selects tuples from Tutorials where the topic is ‘Database’ and ‘author’ is guru99.
Example 3
σ sales > 50000 (Customers)
Output — Selects tuples from Customers where sales is greater than 50000
Projection(π)
The projection eliminates all attributes of the input relation but those mentioned in the projection list. The projection method defines a relation that contains a vertical subset of Relation.
Это помогает извлечь значения указанных атрибутов, чтобы исключить повторяющиеся значения. (pi) Символ, используемый для выбора атрибутов из отношения. Эта операция помогает вам сохранить определенные столбцы от отношения и отбрасывает другие столбцы.
Пример проекции:
Рассмотрим следующую таблицу
| Пользовательский ИД | Имя покупателя | Положение дел |
| 1 | активный | |
| 2 | Амазонка | активный |
| 3 | яблоко | Неактивный |
| 4 | Алибаба | активный |
Здесь проекция CustomerName и статус даст
Π CustomerName, Status (Customers)
| Имя покупателя | Положение дел |
| активный | |
| Амазонка | активный |
| яблоко | Неактивный |
| Алибаба | активный |
Союз операция (у)
СОЮЗ обозначается символом ∪. Он включает в себя все кортежи, которые находятся в таблицах A или B. Он также устраняет дубликаты кортежей. Итак, набор A UNION, набор B, будет выражаться как:
Результат <- A ∪ B
Чтобы операция объединения была действительной, должны выполняться следующие условия:
- R и S должны иметь одинаковое количество атрибутов.
- Домены атрибутов должны быть совместимы.
- Дублирующиеся кортежи должны автоматически удаляться.
пример
Рассмотрим следующие таблицы.
| колонка 1 | колонка 2 | колонка 1 | колонка 2 | |
| 1 | 1 | 1 | 1 | |
| 1 | 2 | 1 | 3 | |
A ∪ B дает
| колонка 1 | колонка 2 |
| 1 | 1 |
| 1 | 2 |
| 1 | 3 |
Установить разницу (-)
— Символ обозначает это. Результатом A — B является отношение, которое включает в себя все кортежи, которые находятся в A, но не в B.
- Имя атрибута A должно совпадать с именем атрибута в B.
- Отношения с двумя операндами A и B должны быть либо совместимыми, либо союзными.
- Должно быть определено отношение, состоящее из кортежей, которые находятся в отношении A, но не в B.
пример
A-B
| колонка 1 | колонка 2 |
| 1 | 2 |
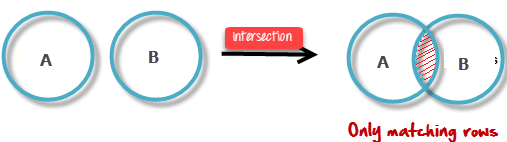
пересечение
Пересечение определяется символом ∩
A ∩ B
Определяет отношение, состоящее из набора всех кортежей в A и B. Однако A и B должны быть совместимы с объединением.
Пример:
A ∩ B
| колонка 1 | колонка 2 |
| 1 | 1 |
Декартово произведение (X)
Этот тип операции полезен для объединения столбцов из двух отношений. Как правило, декартово произведение никогда не является осмысленной операцией, когда оно выполняется в одиночку. Однако это становится значимым, когда за ним следуют другие операции.
Пример — декартово произведение
σ колонок 2 = ‘1’ (А)
Выходные данные — в приведенном выше примере показаны все строки из отношений A и B, столбец 2 которых имеет значение 1
| колонка 1 | колонка 2 |
| 1 | 1 |
| 1 | 1 |
Присоединяйтесь Операции
Операция соединения по существу является декартовым произведением, за которым следует критерий выбора.
Операция присоединения обозначена ⋈.
Операция JOIN также позволяет объединять различные кортежи из разных отношений.
Типы JOIN:
Различные формы операции соединения:
Внутренние соединения:
- Тета присоединиться
- EQUI присоединиться
- Естественное соединение
Внешнее соединение:
- Левое внешнее соединение
- Правое внешнее соединение
- Полное внешнее соединение
Inner Join:
In an inner join, only those tuples that satisfy the matching criteria are included, while the rest are excluded. Let’s study various types of Inner Joins:
Theta Join:
The general case of JOIN operation is called a Theta join. It is denoted by symbol θ
Example
A ⋈θ B
Theta join can use any conditions in the selection criteria.
For example:
A ⋈ A.column 2 > B.column 2 (B)
| column 1 | column 2 |
| 1 | 2 |
EQUI join:
When a theta join uses only equivalence condition, it becomes a equi join.
For example:
A ⋈ A.column 2 = B.column 2 (B)
| column 1 | column 2 |
| 1 | 1 |
EQUI join is the most difficult operations to implement efficiently in an RDBMS and one reason why RDBMS have essential performance problems.
ЕСТЕСТВЕННОЕ СОЕДИНЕНИЕ (⋈)
Естественное объединение может быть выполнено только при наличии общего атрибута (столбца) между отношениями. Имя и тип атрибута должны быть одинаковыми.
пример
Рассмотрим следующие две таблицы
| Num | Квадрат |
| 2 | 4 |
| 3 | 9 |
| Num | куб |
| 2 | 8 |
| 3 | 27 |
C ⋈ D
| Num | Квадрат | куб |
| 2 | 4 | 4 |
| 3 | 9 | 27 |
НАРУЖНОЕ СОЕДИНЕНИЕ
Во внешнем объединении наряду с кортежами, которые удовлетворяют критериям соответствия, мы также включаем некоторые или все кортежи, которые не соответствуют критериям.
Левое внешнее соединение (A  B)
B)
В левом внешнем соединении операция позволяет сохранить весь кортеж в левом отношении. Однако если в правильном отношении не найдено подходящего кортежа, атрибуты правильного отношения в результате объединения заполняются нулевыми значениями.
Рассмотрим следующие 2 таблицы
| Num | Квадрат |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| Num | куб |
| 2 | 8 |
| 3 | 18 |
| 5 | 75 |
AB
| Num | Квадрат | куб |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | — |
Правое внешнее соединение: (A  B)
B)
В правом внешнем соединении операция позволяет сохранить все кортежи в правильном отношении. Однако, если в левом отношении не найдено подходящего кортежа, атрибуты левого отношения в результате объединения заполняются нулевыми значениями.
AB
| Num | куб | Квадрат |
| 2 | 8 | 4 |
| 3 | 18 | 9 |
| 5 | 75 | — |
Полное внешнее соединение: (A  B)
B)
При полном внешнем объединении все кортежи из обоих отношений включаются в результат независимо от условия соответствия.
AB
| Num | куб | Квадрат |
| 2 | 4 | 8 |
| 3 | 9 | 18 |
| 4 | 16 | — |
| 5 | — | 75 |
Резюме
|
операция |
Цель |
|
Выберите (σ) |
Операция SELECT используется для выбора подмножества кортежей в соответствии с заданным условием выбора. |
|
Проекция (π) |
Проекция исключает все атрибуты входного отношения, кроме тех, которые упомянуты в списке проекций. |
|
Союз Операция (∪) |
СОЮЗ символизируется символом. Он включает в себя все кортежи, которые находятся в таблицах A или B. |
|
Установить разницу (-) |
— Символ обозначает это. Результатом A — B является отношение, которое включает в себя все кортежи, которые находятся в A, но не в B. |
|
Пересечение (∩) |
Пересечение определяет отношение, состоящее из набора всех кортежей в A и B. |
|
Декартово произведение (X) |
Декартовая операция полезна для объединения столбцов из двух отношений. |
|
Внутреннее соединение |
Внутреннее объединение включает в себя только те кортежи, которые удовлетворяют критериям соответствия. |
|
Тета Присоединиться (θ) |
Общий случай операции JOIN называется тэта-соединением. Обозначается символом θ. |
|
EQUI Присоединиться |
Когда тэта-соединение использует только условие эквивалентности, оно становится равным соединению. |
|
Естественное соединение (⋈) |
Естественное объединение может быть выполнено только при наличии общего атрибута (столбца) между отношениями. |
|
Внешнее соединение |
Во внешнем соединении вместе с кортежами, которые удовлетворяют критериям соответствия. |
|
В левом внешнем соединении операция позволяет сохранить весь кортеж в левом отношении. |
|
|
В правом внешнем соединении операция позволяет сохранить все кортежи в правильном отношении. |
|
|
В полном внешнем объединении все кортежи из обоих отношений включаются в результат независимо от условия соответствия. |
 B)
B)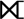 B)
B)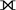 B)
B)