Учебники

PyTorch — рекуррентная нейронная сеть

Апрель 1, 2019

Рекуррентные нейронные сети — это один тип алгоритма, ориентированного на глубокое обучение, который следует последовательному подходу. В нейронных сетях мы всегда предполагаем, что каждый вход и выход не зависит от всех других слоев. Нейронные сети такого типа называются рекуррентными, поскольку они выполняют математические вычисления последовательно, выполняя одну задачу за другой.

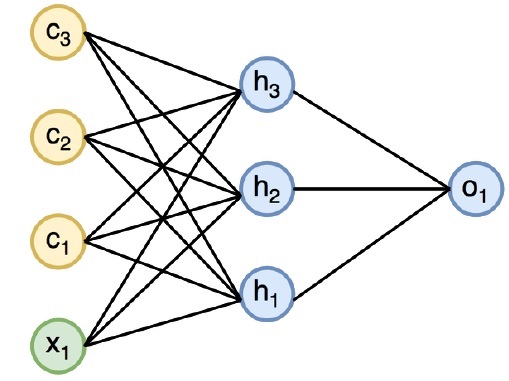
Диаграмма ниже определяет полный подход и работу рекуррентных нейронных сетей —

Рекуррентные Нейронные сети Ex

На приведенном выше рисунке c1, c2, c3 и x1 рассматриваются как входные данные, которые включают в себя некоторые скрытые входные значения, а именно h1, h2 и h3, обеспечивающие соответствующий выходной сигнал o1. Теперь мы сосредоточимся на реализации PyTorch для создания синусоиды с помощью рекуррентных нейронных сетей.

Во время обучения мы будем следовать обучающему подходу к нашей модели с одной точкой данных за раз. Входная последовательность x состоит из 20 точек данных, и целевая последовательность считается такой же, как входная последовательность.

Шаг 1

Импортируйте необходимые пакеты для реализации рекуррентных нейронных сетей, используя следующий код — 

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

Шаг 2

Мы установим гиперпараметры модели с размером входного слоя 7. Для создания целевой последовательности будет 6 контекстных нейронов и 1 входной нейрон. 

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

Мы сгенерируем обучающие данные, где x — последовательность входных данных, а y — требуемая последовательность.

Шаг 3

Веса инициализируются в рекуррентной нейронной сети с использованием нормального распределения с нулевым средним. W1 будет представлять принятие входных переменных, а w2 будет представлять вывод, который генерируется, как показано ниже — 

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

Шаг 4

Теперь важно создать функцию для прямой связи, которая однозначно определяет нейронную сеть. 

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

Шаг 5

Следующим шагом является запуск процедуры обучения реализации синусоидальной волны в текущей нейронной сети. Внешний цикл повторяется по каждому циклу, а внутренний цикл повторяется по элементу последовательности. Здесь мы также вычислим среднеквадратичную ошибку (MSE), которая помогает в прогнозировании непрерывных переменных. 

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j🙁j+1)]
      target = y[j🙁j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

Шаг 6

Теперь пришло время построить синусоидальную волну так, как она нужна. 

pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

Выход

Выход для вышеуказанного процесса выглядит следующим образом:

66
Share: