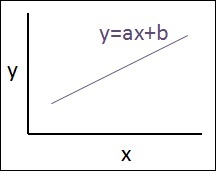Учебники

PyTorch — линейная регрессия

Апрель 1, 2019

В этой главе мы сосредоточимся на базовом примере реализации линейной регрессии с использованием TensorFlow. Логистическая регрессия или линейная регрессия — это контролируемый подход машинного обучения для классификации категорий дискретных порядков. Наша цель в этой главе — создать модель, с помощью которой пользователь может предсказать взаимосвязь между переменными предиктора и одной или несколькими независимыми переменными.

Соотношение между этими двумя переменными считается линейным, т. Е. Если y является зависимой переменной, а x рассматривается как независимая переменная, то отношение линейной регрессии двух переменных будет выглядеть как уравнение, которое упоминается ниже: 

Y = Ax+b

Далее мы разработаем алгоритм линейной регрессии, который позволит нам понять две важные концепции, приведенные ниже:

  • Функция стоимости
  • Алгоритмы градиентного спуска

Схематическое представление линейной регрессии упоминается ниже

Интерпретация результата

Y=ах+Ь

  • Значение а является наклоном.

  • Значение b — это y — пересечение .

  • r — коэффициент корреляции .

  • r 2 — коэффициент корреляции .

Значение а является наклоном.

Значение b — это y — пересечение .

r — коэффициент корреляции .

r 2 — коэффициент корреляции .

Графическое представление уравнения линейной регрессии упоминается ниже —

Интерпретация результата

Следующие шаги используются для реализации линейной регрессии с использованием PyTorch —

Шаг 1

Импортируйте необходимые пакеты для создания линейной регрессии в PyTorch, используя следующий код — 

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Шаг 2

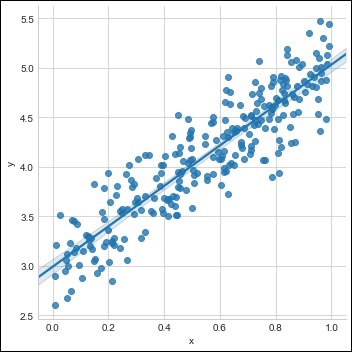
Создайте единый тренировочный набор с доступным набором данных, как показано ниже — 

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)

Одиночное обучение

Шаг 3

Реализуйте линейную регрессию с библиотеками PyTorch, как упомянуто ниже — 

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

Сюжет генерируется следующим образом —

54
Share: