Микроволновая техника — Микроволновые устройства

Как и другие системы, микроволновые системы состоят из множества микроволновых компонентов, в основном с источником на одном конце и нагрузкой на другом, которые все связаны с волноводами или коаксиальным кабелем или системами линий электропередачи.

Ниже приведены свойства волноводов.

• Высокий SNR
• Низкое затухание
• Более низкая вносимая потеря

Волноводные СВЧ-функции

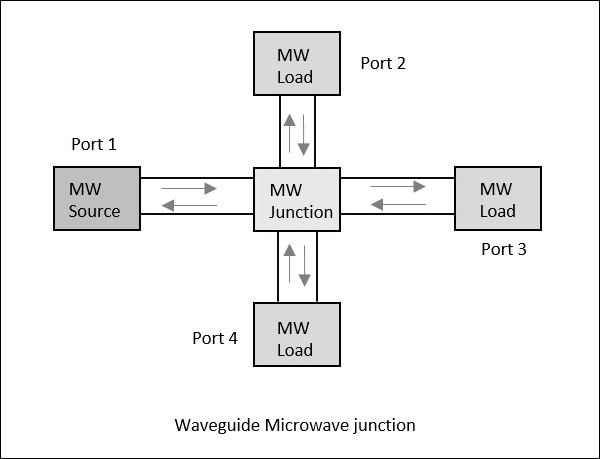
Рассмотрим волновод, имеющий 4 порта. Если питание подается на один порт, оно проходит через все 3 порта в некоторых пропорциях, где часть из них может отражаться от одного и того же порта. Эта концепция четко изображена на следующем рисунке.

Параметры рассеяния

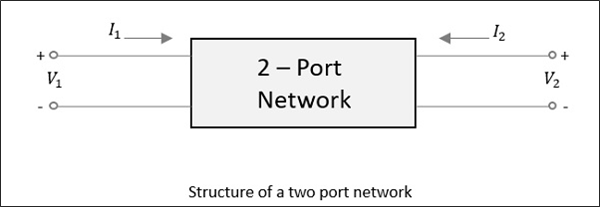
Для сети с двумя портами, как показано на следующем рисунке, если питание подается на один порт, как мы только что обсуждали, большая часть мощности выходит из другого порта, а часть отражается обратно на тот же порт. На следующем рисунке, если применяется V ₁ или V ₂ , то ток I ₁ или I ₂ протекает соответственно.

Если источник применяется к противоположному порту, следует рассмотреть еще две комбинации. Таким образом, для сети с двумя портами, вероятно, могут возникнуть комбинации 2 × 2 = 4.

Бегущие волны с соответствующими мощностями при рассеянии через порты СВЧ-соединения могут быть определены S-параметрами или параметрами рассеяния , которые представлены в виде матрицы, называемой « Матрица рассеяния ».

Матрица рассеяния

Это квадратная матрица, которая дает все комбинации соотношений мощности между различными входными и выходными портами микроволнового соединения. Элементы этой матрицы называются «коэффициентами рассеяния» или «параметрами рассеяния (S)» .

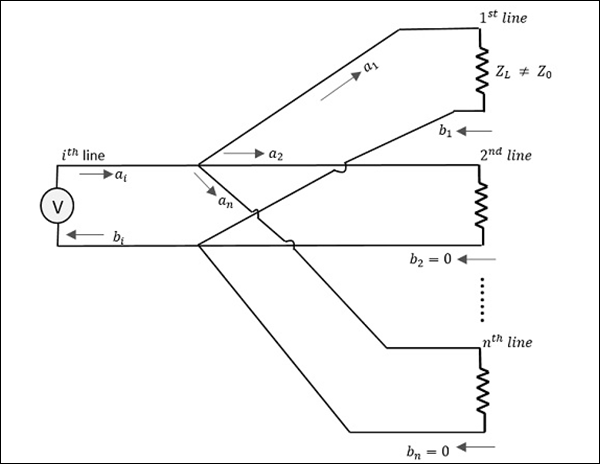
Рассмотрим следующий рисунок.

Здесь источник соединен линией $i ^ {th}$, а $a_1$ — падающая волна, а $b_1$ — отраженная волна.

Если дана связь между $b_1$ и $a_1$,

b1=(отражениекоэффициент)a1=S1ia1 $$b_1 = (отражение \: \: коэффициент) a_1 = S_ {1i} a_1$$

куда

• $S_ {1i}$ = коэффициент отражения линии $1 ^ {st}$ (где $i$ — входной порт, а $1$ — выходной порт)

• $1$ = Отражение от линии $1 ^ {st}$

• $i$ = Источник подключен к линии $i ^ {th}$

$S_ {1i}$ = коэффициент отражения линии $1 ^ {st}$ (где $i$ — входной порт, а $1$ — выходной порт)

$1$ = Отражение от линии $1 ^ {st}$

$i$ = Источник подключен к линии $i ^ {th}$

Если полное сопротивление совпадает, то мощность передается на нагрузку. Маловероятно, если сопротивление нагрузки не совпадает с характеристическим сопротивлением. Затем происходит отражение. Это означает, что отражение происходит, если

$$Z_l \ neq Z_o$$

Однако, если это несоответствие существует для более чем одного порта, например портов ′n′$'n'$, то от $i = 1$ до $n$ (поскольку $i$ может быть любой строкой от $1$ до $n$).

Поэтому мы имеем

$$b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n$$

$$b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n$$

.

.

.

.

.

$$b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n$$

Когда все это хранится в матричной форме,

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & … & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & … & S_ {2n} \\. &. &. & … &. \\. &. &. & … &. \\. &. &. & … &. \\ S_ {n1} & S_ {n2} & S_ {n3} & … & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$

Матрица столбца $[b]$ Матрица рассеяния $[S]$ Матрица $[a]$

Матрица столбца $\ left [b \ right]$ соответствует отраженным волнам или выходному сигналу, а матрица $\ left [a \ right]$ соответствует падающим волнам или входному сигналу. Матрица рассеивающего столбца $\ left [s \ right]$ порядка $n \ times n$ содержит коэффициенты отражения и коэффициенты пропускания. Следовательно,

$$\ left [b \ right] = \ left [S \ right] \ left [a \ right]$$

Свойства матрицы [S]

Матрица рассеяния указана в виде матрицы $[S]$. Существует несколько стандартных свойств для матрицы $[S]$. Они —

• $[S]$ всегда квадратная матрица порядка (nxn)

  $[S] _ {n \ times n}$

• $[S]$ — симметричная матрица

  то есть $S_ {ij} = S_ {ji}$

• $[S]$ — унитарная матрица

  т.е. $[S] [S] ^ * = I$

• Сумма произведений каждого члена любой строки или столбца, умноженная на комплексное сопряжение соответствующих членов любой другой строки или столбца, равна нулю. т.е.

$[S]$ всегда квадратная матрица порядка (nxn)

$[S] _ {n \ times n}$

$[S]$ — симметричная матрица

то есть $S_ {ij} = S_ {ji}$

$[S]$ — унитарная матрица

т.е. $[S] [S] ^ * = I$

Сумма произведений каждого члена любой строки или столбца, умноженная на комплексное сопряжение соответствующих членов любой другой строки или столбца, равна нулю. т.е.

 sumni=jSikS∗ik=0дляk neqj $$\ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: для \: k \ neq j$$

(k=1,2,3,...n)и(j=1,2,3,...n) $$(k = 1,2,3, ... \: n) \: и \: (j = 1,2,3, ... \: n)$$

• Если электрическое расстояние между портом $k ^ {th}$ и переходом равно $\ beta _kI_k$, то коэффициенты $S_ {ij}$, включающие $k$, будут умножены на коэффициент $e ^ {- j \ beta kIk}$

Если электрическое расстояние между портом $k ^ {th}$ и переходом равно $\ beta _kI_k$, то коэффициенты $S_ {ij}$, включающие $k$, будут умножены на коэффициент $e ^ {- j \ beta kIk}$

В следующих нескольких главах мы рассмотрим различные типы соединений СВЧ-тройников.