Микроволновая инженерия — H-Plane Tee

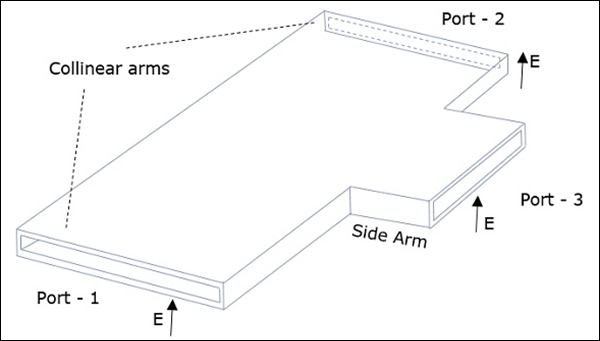
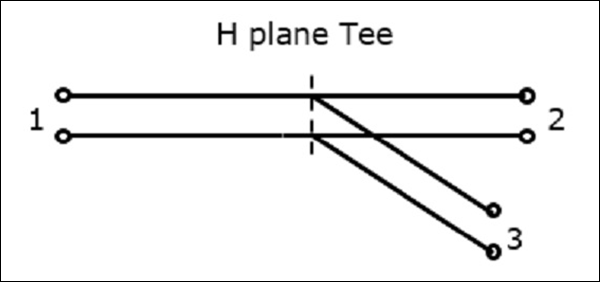
Соединение тройника H-плоскости формируется путем присоединения простого волновода к прямоугольному волноводу, который уже имеет два порта. Плечи прямоугольных волноводов образуют два порта, называемые коллинеарными портами, т. Е. Port1 и Port2, а новый порт Port3 называется боковым или H-плечом . Эта тройник Н-плоскости также называется шунтирующей .

Поскольку ось бокового рычага параллельна магнитному полю, этот переход называется тройником H-плоскости. Это также называется Токовым переходом , поскольку магнитное поле делится на плечи. Детали поперечного сечения тройника H-плоскости можно понять из следующего рисунка.

На следующем рисунке показано соединение, выполненное боковым рычагом с двунаправленным волноводом для формирования последовательного порта.

Свойства тройника H-Plane

Свойства H-плоскости Tee могут быть определены его  left[S right]3 times3$\ left [S \ right] _ {3 \ times 3}$ матрицей.

Это матрица 3 × 3, так как есть 3 возможных входа и 3 возможных выхода.

[S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix}$[S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix}$ …….. Уравнение 1

Коэффициенты рассеяния S13$S_ {13}$ и S23$S_ {23}$ здесь равны, поскольку переход симметричен на плоскости.

Из симметричного свойства,

Sij=Sji$S_ {ij} = S_ {ji}$

S12=S21S23=S32=S13S13=S31$S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} = S_ {13} \: \: S_ {13} = S_ {31}$

Порт идеально подобран

S33=0$S_ {33} = 0$

Теперь матрицу [S]$[S]$ можно записать в виде

[S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13 } & 0 \ end {bmatrix}$[S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13 } & 0 \ end {bmatrix}$ …….. Уравнение 2

Можно сказать, что у нас есть четыре неизвестных, учитывая свойство симметрии.

От унитарной собственности

[S][S] ast=[I]

$$[S] [S] \ ast = [I]$$

\ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}

$$\ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}$$

Умножая мы получаем,

(Отмечая R как строку и C как столбец)

R1C1:S11S∗11+S12S∗12+S13S∗13=1$R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1$

$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $ …….. Уравнение 3

$ R_2C_2: \ left | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $ ……… Уравнение 4

$ R_3C_3: \ left | S_ {13} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $ ……… Уравнение 5

R3C1:S13S∗11−S13S∗12=0$R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 0$ ……… Уравнение 6

$ 2 \ слева | S_ {13} \ right | ^ 2 = 1 \ quad или \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $ ……… Уравнение 7

$ \ left | S_ {11} \ right | ^ 2 = \ left | S_ {22} \ right | ^ 2 $

S11=S22$S_ {11} = S_ {22}$ ……… Уравнение 8

Из уравнения 6 S13 left(S∗11+S∗12 right)=0$S_ {13} \ left (S_ {11} ^ {*} + S_ {12} ^ {*} \ right) = 0$

Так как S13 neq0,S∗11+S∗12=0,илиS∗11=−S∗12$S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: или \: S_ {11} ^ {*} = -S_ {12} ^ {*}$

Или S11=−S12илиS12=−S11$S_ {11} = -S_ {12} \: \: или \: \: S_ {12} = -S_ {11}$ ……… Уравнение 9

Используя их в уравнении 3,

Так как S13 neq0,S∗11+S∗12=0,илиS∗11=−S∗12$S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: или \: S_ {11} ^ {*} = -S_ {12} ^ {*}$

$ \ left | S_ {11} \ right | ^ 2 + \ left | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 \ quad или \ quad 2 \ left | S_ {11} \ right | ^ 2 = \ frac {1} {2} \ quad или \ quad S_ {11} = \ frac {1} {2} $ ….. Уравнение 10

Из уравнений 8 и 9

S12=− frac12$S_ {12} = - \ frac {1} {2}$ ……… Уравнение 11

S22= frac12$S_ {22} = \ frac {1} {2}$ ……… Уравнение 12

Подставляя для S13$S_ {13}$, S11$S_ {11}$, S12$S_ {12}$ и S22$S_ {22}$ из уравнений 7 и 10, 11 и 12 в уравнение 2,

Мы получаем,

\ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & — \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ — \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix}

$$\ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix}$$

Мы знаем, что [b]$[b]$ = [s][a]$[s] [a]$

\ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & — \ frac {1} {2} & \ frac {1} { \ sqrt {2}} \\ — \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix}

$$\ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} { \ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix}$$

Это матрица рассеяния для H-плоскости Tee, которая объясняет ее рассеивающие свойства.