Учебники

SciPy — ODR

Март 26, 2019

ODR обозначает регрессию ортогонального расстояния , которая используется в исследованиях регрессии. Базовая линейная регрессия часто используется для оценки взаимосвязи между двумя переменными y и x путем рисования линии наилучшего соответствия на графике.

Математический метод, который используется для этого, известен как наименьшие квадраты и направлен на минимизацию суммы квадратов ошибок для каждой точки. Ключевой вопрос здесь заключается в том, как рассчитать ошибку (также известную как остаток) для каждой точки?

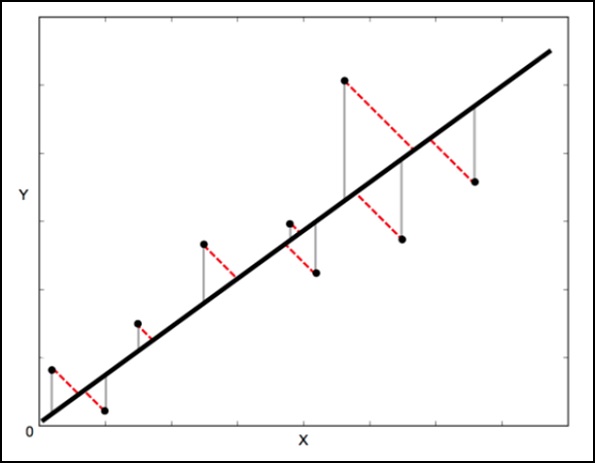
В стандартной линейной регрессии цель состоит в том, чтобы предсказать значение Y по значению X, поэтому разумно будет рассчитать погрешность в значениях Y (показано серыми линиями на следующем изображении). Тем не менее, иногда разумнее учитывать ошибку как в X, так и в Y (как показано пунктирными красными линиями на следующем изображении).

Например — когда вы знаете, что ваши измерения X неопределенны или когда вы не хотите сосредоточиться на ошибках одной переменной над другой.

Ортогональное расстояние линейная регрессия

Ортогональная регрессия расстояния (ODR) — это метод, который может сделать это (ортогональный в данном контексте означает перпендикулярный — поэтому он вычисляет ошибки перпендикулярно линии, а не просто «вертикально»).

Реализация scipy.odr для одномерной регрессии

В следующем примере демонстрируется реализация scipy.odr для одномерной регрессии. 

import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random

# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])

# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
   m, c = p
   return m*x + c

# Create a model for fitting.
linear_model = Model(linear_func)

# Create a RealData object using our initiated data from above.
data = RealData(x, y)

# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])

# Run the regression.
out = odr.run()

# Use the in-built pprint method to give us results.
out.pprint()

Вышеуказанная программа сгенерирует следующий вывод.

50
Share: