CSGraph расшифровывается как Compressed Sparse Graph , который фокусируется на алгоритмах Fast графа, основанных на разреженных матричных представлениях.
Графические представления
Для начала давайте разберемся, что такое разреженный граф и как он помогает в представлении графов.
Что такое разреженный граф?
Граф — это просто набор узлов, между которыми есть связи. Графики могут представлять почти все — соединения в социальных сетях, где каждый узел является личностью и связан со знакомыми; изображения, где каждый узел является пикселем и связан с соседними пикселями; точки в многомерном распределении, где каждый узел связан со своими ближайшими соседями; и практически все, что вы можете себе представить.
Один очень эффективный способ представления данных графа — это разреженная матрица: назовем ее G. Матрица G имеет размер N x N, а G [i, j] дает значение связи между узлом «i» и узлом. ‘J’. Разреженный граф содержит в основном нули, то есть большинство узлов имеют только несколько соединений. Это свойство оказывается истинным в большинстве случаев, представляющих интерес.
Создание подмодуля разреженного графа было мотивировано несколькими алгоритмами, использованными в scikit-learn, которые включали следующее:
-
Isomap — алгоритм обучения многообразия, который требует нахождения кратчайших путей в графе.
-
Иерархическая кластеризация — алгоритм кластеризации, основанный на минимальном остовном дереве.
-
Спектральная декомпозиция — алгоритм проекции, основанный на лапласианах разреженных графов.
Isomap — алгоритм обучения многообразия, который требует нахождения кратчайших путей в графе.
Иерархическая кластеризация — алгоритм кластеризации, основанный на минимальном остовном дереве.
Спектральная декомпозиция — алгоритм проекции, основанный на лапласианах разреженных графов.
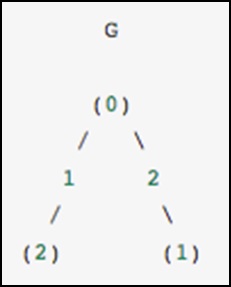
В качестве конкретного примера представьте, что мы хотели бы представить следующий неориентированный граф:
Этот граф имеет три узла, где узлы 0 и 1 соединены ребром веса 2, а узлы 0 и 2 соединены ребром веса 1. Мы можем построить плотные, замаскированные и разреженные представления, как показано в следующем примере. , имея в виду, что ненаправленный граф представлен симметричной матрицей.
G_dense = np.array([ [0, 2, 1], [2, 0, 0], [1, 0, 0] ]) G_masked = np.ma.masked_values(G_dense, 0) from scipy.sparse import csr_matrix G_sparse = csr_matrix(G_dense) print G_sparse.data
Вышеуказанная программа сгенерирует следующий вывод.
array([2, 1, 2, 1])
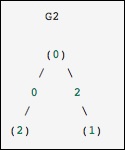
Это идентично предыдущему графику, за исключением того, что узлы 0 и 2 соединены ребром нулевого веса. В этом случае представленное выше плотное представление приводит к неоднозначности — как можно представить не-ребра, если ноль является значимым значением. В этом случае либо маскированное, либо разреженное представление должно использоваться для устранения неоднозначности.
Давайте рассмотрим следующий пример.
from scipy.sparse.csgraph import csgraph_from_dense G2_data = np.array ([ [np.inf, 2, 0 ], [2, np.inf, np.inf], [0, np.inf, np.inf] ]) G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf) print G2_sparse.data
Вышеуказанная программа сгенерирует следующий вывод.
array([ 2., 0., 2., 0.])
Лестницы слов с использованием разреженных графов
Word ladders — это игра, изобретенная Льюисом Кэрроллом, в которой слова связаны между собой изменением одной буквы на каждом шаге. Например —
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Здесь мы перешли от «APE» к «MAN» за семь шагов, каждый раз меняя одну букву. Вопрос в том, можем ли мы найти более короткий путь между этими словами, используя одно и то же правило? Эта проблема естественно выражается как проблема разреженных графов. Узлы будут соответствовать отдельным словам, и мы создадим связи между словами, которые различаются не более чем на одну букву.
Получение списка слов
Во-первых, конечно, мы должны получить список допустимых слов. Я использую Mac, и Mac имеет словарь слов в месте, указанном в следующем блоке кода. Если вы используете другую архитектуру, вам, возможно, придется немного поискать, чтобы найти системный словарь.
wordlist = open('/usr/share/dict/words').read().split() print len(wordlist)
Вышеуказанная программа сгенерирует следующий вывод.
235886
Теперь мы хотим взглянуть на слова длиной 3, поэтому давайте выберем только те слова правильной длины. Мы также исключим слова, которые начинаются с верхнего регистра (собственно существительные) или содержат не алфавитно-цифровые символы, такие как апострофы и дефисы. Наконец, мы убедимся, что все будет в нижнем регистре для сравнения позже.
word_list = [word for word in word_list if len(word) == 3] word_list = [word for word in word_list if word[0].islower()] word_list = [word for word in word_list if word.isalpha()] word_list = map(str.lower, word_list) print len(word_list)
Вышеуказанная программа сгенерирует следующий вывод.
1135
Теперь у нас есть список из 1135 правильных трехбуквенных слов (точное число может меняться в зависимости от конкретного используемого списка). Каждое из этих слов станет узлом в нашем графе, и мы создадим ребра, соединяющие узлы, связанные с каждой парой слов, которые отличаются только одной буквой.
import numpy as np word_list = np.asarray(word_list) word_list.dtype word_list.sort() word_bytes = np.ndarray((word_list.size, word_list.itemsize), dtype = 'int8', buffer = word_list.data) print word_bytes.shape
Вышеуказанная программа сгенерирует следующий вывод.
(1135, 3)
Мы будем использовать расстояние Хэмминга между каждой точкой, чтобы определить, какие пары слов связаны. Расстояние Хэмминга измеряет долю записей между двумя векторами, которые различаются: любые два слова с расстоянием Хэмминга, равным 1 / N1 / N, где NN — количество букв, которые связаны в словарной лестнице.
from scipy.spatial.distance import pdist, squareform from scipy.sparse import csr_matrix hamming_dist = pdist(word_bytes, metric = 'hamming') graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))
При сравнении расстояний мы не используем равенство, потому что это может быть нестабильно для значений с плавающей запятой. Неравенство дает желаемый результат до тех пор, пока никакие две записи в списке слов не являются идентичными. Теперь, когда наш граф настроен, мы будем использовать поиск кратчайшего пути, чтобы найти путь между любыми двумя словами в графе.
i1 = word_list.searchsorted('ape') i2 = word_list.searchsorted('man') print word_list[i1],word_list[i2]
Вышеуказанная программа сгенерирует следующий вывод.
ape, man
Мы должны проверить, что они совпадают, потому что, если слова не находятся в списке, в выходных данных будет ошибка. Теперь все, что нам нужно, это найти кратчайший путь между этими двумя индексами в графе. Мы будем использовать алгоритм Дейкстры, потому что он позволяет нам найти путь только для одного узла.
from scipy.sparse.csgraph import dijkstra distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True) print distances[i2]
Вышеуказанная программа сгенерирует следующий вывод.
5.0
Таким образом, мы видим, что кратчайший путь между «обезьяной» и «человеком» содержит всего пять шагов. Мы можем использовать предшественников, возвращаемых алгоритмом, чтобы восстановить этот путь.
path = [] i = i2 while i != i1: path.append(word_list[i]) i = predecessors[i] path.append(word_list[i1]) print path[::-1]i2]
Вышеуказанная программа сгенерирует следующий вывод.