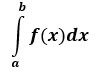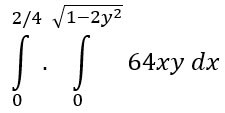Что такое SciPy?
SciPy — это библиотека на основе Python с открытым исходным кодом, которая используется в математике, научных вычислениях, технике и технических вычислениях.
SciPy также произносится как «Вздох Пи».
Подпакеты SciPy:
- Ввод / вывод файла — scipy.io
- Специальная функция — scipy.special
- Операция по линейной алгебре — scipy.linalg
- Интерполяция — scipy.interpolate
- Оптимизация и подгонка — scipy.optimize
- Статистика и случайные числа — scipy.stats
- Численная интеграция — scipy.integrate
- Быстрые преобразования Фурье — scipy.fftpack
- Обработка сигналов — scipy.signal
- Работа с изображениями — scipy.ndimage
В этом уроке вы узнаете:
- Что такое SciPy?
- Зачем использовать SciPy
- Numpy VS SciPy
- SciPy — Установка и настройка среды
- Пакет ввода / вывода файла:
- Специальный пакет функций:
- Линейная алгебра с SciPy:
- Дискретное преобразование Фурье — scipy.fftpack
- Оптимизация и встраивание в SciPy — scipy.optimize
- Алгоритм Нелдера-Мида:
- Обработка изображений с помощью SciPy — scipy.ndimage
Зачем использовать SciPy
- SciPy содержит множество подпакетов, которые помогают решить наиболее распространенную проблему, связанную с научными вычислениями.
- SciPy является наиболее используемой научной библиотекой, уступающей только научной библиотеке GNU для C / C ++ или Matlab.
- Простой в использовании и понимании, а также быстрая вычислительная мощность.
- Он может работать с массивом библиотеки NumPy.
Numpy VS SciPy
Numpy:
- Numpy написан на C и используется для математических или численных расчетов.
- Это быстрее, чем другие библиотеки Python
- Numpy — самая полезная библиотека для Data Science для выполнения базовых вычислений.
- Numpy не содержит ничего, кроме типа данных массива, который выполняет самые основные операции, такие как сортировка, формирование, индексация и т. Д.
SciPy:
- SciPy построен на вершине NumPy
- SciPy — это полнофункциональная версия линейной алгебры, в то время как Numpy содержит только несколько функций.
- Большинство новых функций Data Science доступно в Scipy, а не в Numpy.
SciPy — Установка и настройка среды
Вы также можете установить SciPy в Windows через pip
Python3 -m pip install --user numpy scipy
Установите Scipy на Linux
sudo apt-get install python-scipy python-numpy
Установите SciPy в Mac
sudo port install py35-scipy py35-numpy
Прежде чем приступить к изучению SciPy, вам необходимо знать основные функциональные возможности, а также различные типы массивов NumPy.
Стандартный способ импорта модулей infSciPy и Numpy:
from scipy import special #same for other modules import numpy as np
Пакет ввода / вывода файла:
Scipy, пакет ввода / вывода, обладает широким набором функций для работы с различными форматами файлов: Matlab, Arff, Wave, Matrix Market, IDL, NetCDF, TXT, CSV и двоичным форматом.
Давайте возьмем один пример формата файла, который регулярно использует MatLab:
import numpy as np
from scipy import io as sio
array = np.ones((4, 4))
sio.savemat('example.mat', {'ar': array})
data = sio.loadmat(‘example.mat', struct_as_record=True)
data['ar']
Вывод:
array([[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
Код Объяснение
- Строки 1 и 2: импортируйте необходимую библиотеку scipy с пакетом ввода-вывода и Numpy.
- Строка 3 : Создать 4 x 4, размерный массив
- Строка 4 : сохранить массив в файле example.mat .
- Строка 5: получить данные из файла example.mat
- Строка 6 : вывод на печать.
Пакет специальных функций
- Пакет scipy.special содержит множество функций математической физики.
- Специальная функция SciPy включает в себя кубический корень, экспоненциальный, логарифмический экспоненциальный, ламберт, перестановку и комбинации, гамму, бесселеву, гипергеометрический, кельвин, бета, параболический цилиндр, относительную погрешность и т. Д.
- Чтобы в одной строке описать все эти функции, введите в консоли Python:
help(scipy.special)
Output :
NAME
scipy.special
DESCRIPTION
========================================
Special functions (:mod:`scipy.special`)
========================================
.. module:: scipy.special
Nearly all of the functions below are universal functions and follow
broadcasting and automatic array-looping rules. Exceptions are noted.
Кубическая корневая функция:
Функция Cubic Root находит корень куба значений.
Синтаксис:
scipy.special.cbrt(x)
Пример:
from scipy.special import cbrt #Find cubic root of 27 & 64 using cbrt() function cb = cbrt([27, 64]) #print value of cb print(cb)
Вывод: массив ([3., 4.])
Экспоненциальная функция:
Экспоненциальная функция вычисляет 10 ** х поэлементно.
Пример:
from scipy.special import exp10 #define exp10 function and pass value in its exp = exp10([1,10]) print(exp)
Выход: [1.e + 01 1.e + 10]
Перестановки и комбинации:
SciPy также предоставляет функциональность для расчета перестановок и комбинаций.
Комбинации — scipy.special.comb (N, k )
Пример:
from scipy.special import comb #find combinations of 5, 2 values using comb(N, k) com = comb(5, 2, exact = False, repetition=True) print(com)
Выход: 15.0
Перестановки —
scipy.special.perm(N,k)
Пример:
from scipy.special import perm #find permutation of 5, 2 using perm (N, k) function per = perm(5, 2, exact = True) print(per)
Выход: 20
Экспоненциальная функция логарифмической суммы
Log Sum Exponential вычисляет логарифм суммы экспоненциального входного элемента.
Синтаксис:
scipy.special.logsumexp(x)
Функция Бесселя
Функция вычисления N-го целого порядка
Синтаксис:
scipy.special.jn()
Линейная алгебра с SciPy
- Линейная алгебра SciPy — это реализация библиотек BLAS и ATLAS LAPACK.
- Производительность линейной алгебры очень быстрая по сравнению с BLAS и LAPACK.
- Подпрограмма линейной алгебры принимает объект двумерного массива, и вывод также является двумерным массивом.
Теперь давайте проведем тест с scipy.linalg,
Вычисление определителя двумерной матрицы,
from scipy import linalg import numpy as np #define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass values to det() function linalg.det( two_d_array )
Выход: -7.0
Обратная матрица —
scipy.linalg.inv()
Обратная матрица Сципи вычисляет обратную матрицу.
Посмотрим,
from scipy import linalg import numpy as np # define square matrix two_d_array = np.array([ [4,5], [3,2] ]) #pass value to function inv() linalg.inv( two_d_array )
Вывод:
array( [[-0.28571429, 0.71428571],
[ 0.42857143, -0.57142857]] )
Собственные значения и собственный вектор — scipy.linalg.eig ()
- Наиболее распространенная проблема в линейной алгебре — это собственные значения и собственный вектор, которые легко решаются с помощью функции eig () .
- Теперь давайте найдем собственное значение ( X ) и соответствующий собственный вектор двумерной квадратной матрицы.
Пример,
from scipy import linalg import numpy as np #define two dimensional array arr = np.array([[5,4],[6,3]]) #pass value into function eg_val, eg_vect = linalg.eig(arr) #get eigenvalues print(eg_val) #get eigenvectors print(eg_vect)
Вывод:
[ 9.+0.j -1.+0.j] #eigenvalues [ [ 0.70710678 -0.5547002 ] #eigenvectors [ 0.70710678 0.83205029] ]
Дискретное преобразование Фурье — scipy.fftpack
- DFT — это математический метод, который используется для преобразования пространственных данных в частотные данные.
- БПФ (быстрое преобразование Фурье) представляет собой алгоритм для вычисления ДПФ
- БПФ применяется к многомерному массиву.
- Частота определяет количество сигнала или длину волны в конкретный период времени.
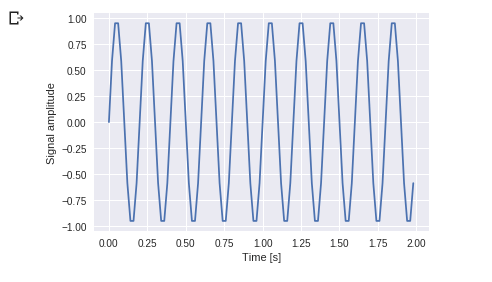
Пример: возьмите волну и покажите, используя библиотеку Matplotlib. мы берем простой периодический пример функции sin (20 × 2πt)
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
#Frequency in terms of Hertz
fre = 5
#Sample rate
fre_samp = 50
t = np.linspace(0, 2, 2 * fre_samp, endpoint = False )
a = np.sin(fre * 2 * np.pi * t)
figure, axis = plt.subplots()
axis.plot(t, a)
axis.set_xlabel ('Time (s)')
axis.set_ylabel ('Signal amplitude')
plt.show()
Вывод :
Вы можете видеть это. Частота составляет 5 Гц, и ее сигнал повторяется через 1/5 секунды — это вызов как определенный период времени.
Теперь давайте использовать эту синусоидальную волну с помощью приложения DFT.
from scipy import fftpack
A = fftpack.fft(a)
frequency = fftpack.fftfreq(len(a)) * fre_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-fre_samp / 2, fre_samp/ 2)
axis.set_ylim(-5, 110)
plt.show()
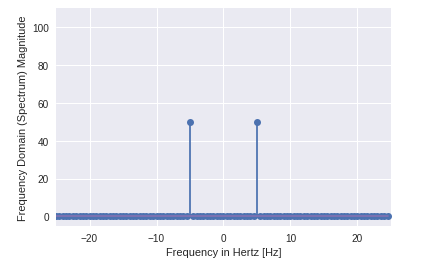
Вывод:
- Вы можете ясно видеть, что выходные данные являются одномерным массивом.
- Входные данные, содержащие комплексные значения, равны нулю, кроме двух точек.
- В примере DFT мы визуализируем величину сигнала.
Оптимизация и встраивание в SciPy — scipy.optimize
- Оптимизация предоставляет полезный алгоритм для минимизации подгонки кривой, многомерной или скалярной и корневой подгонки.
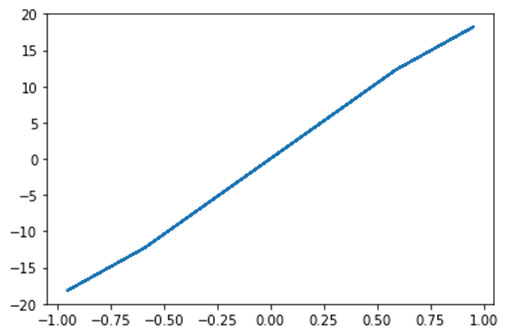
- Давайте возьмем пример скалярной функции, чтобы найти минимальную скалярную функцию .
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import optimize
import numpy as np
def function(a):
return a*2 + 20 * np.sin(a)
plt.plot(a, function(a))
plt.show()
#use BFGS algorithm for optimization
optimize.fmin_bfgs(function, 0)
Вывод:
Оптимизация успешно завершена.
Текущее значение функции: -23.241676
Итерации: 4
Оценка функций: 18
Оценка градиента: 6
Массив ([- 1,67096375])
- В этом примере оптимизация выполняется с помощью алгоритма градиентного спуска с начальной точки.
- Но возможная проблема — локальные минимумы вместо глобальных минимумов. Если мы не найдем соседа глобальных минимумов, то нам нужно применить глобальную оптимизацию и найти функцию глобальных минимумов, используемую в качестве bashopping (), которая объединяет локальный оптимизатор.
optimize.basinhopping (функция, 0)
Вывод:
fun: -23.241676238045315
lowest_optimization_result:
fun: -23.241676238045315
hess_inv: array([[0.05023331]])
jac: array([4.76837158e-07])
message: 'Optimization terminated successfully.'
nfev: 15
nit: 3
njev: 5
status: 0
success: True
x: array([-1.67096375])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 1530
nit: 100
njev: 510
x: array([-1.67096375])
Алгоритм Нелдера-Мида:
- Алгоритм Нелдера-Мида выбирает через параметр метода.
- Это обеспечивает наиболее простой способ минимизации справедливого поведения.
- Алгоритм Нелдера — Мида не используется для оценки градиента, потому что может потребоваться больше времени, чтобы найти решение.
import numpy as np
from scipy.optimize import minimize
#define function f(x)
def f(x):
return .4*(1 - x[0])**2
optimize.minimize(f, [2, -1], method="Nelder-Mead")
Вывод:
final_simplex: (array([[ 1. , -1.27109375],
[ 1. , -1.27118835],
[ 1. , -1.27113762]]), array([0., 0., 0.]))
fun: 0.0
message: 'Optimization terminated successfully.'
nfev: 147
nit: 69
status: 0
success: True
x: array([ 1. , -1.27109375])
Обработка изображений с помощью SciPy — scipy.ndimage
- scipy.ndimage — это подмодуль SciPy, который в основном используется для выполнения операций с изображениями
- ndimage означает «n» размерное изображение.
- SciPy Image Processing обеспечивает преобразование геометрии (поворот, обрезка, отражение), фильтрацию изображения (резкое и четкое), отображение изображения, сегментацию изображения, классификацию и извлечение признаков.
- Пакет MISC в SciPy содержит готовые изображения, которые можно использовать для выполнения задач по обработке изображений
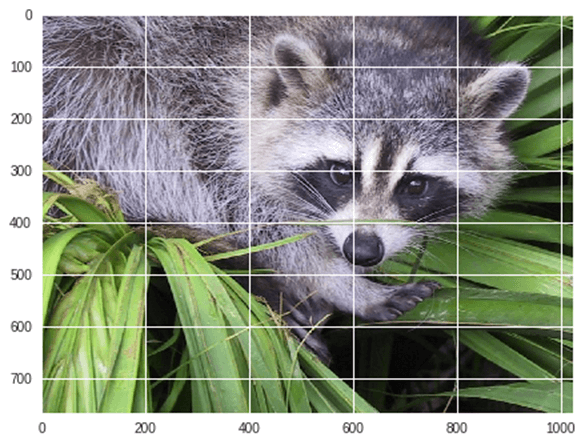
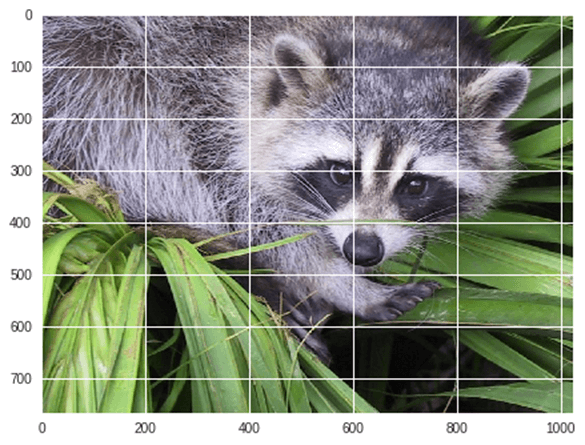
Пример: Давайте возьмем пример геометрического преобразования изображений
from scipy import misc from matplotlib import pyplot as plt import numpy as np #get face image of panda from misc package panda = misc.face() #plot or show image of face plt.imshow( panda ) plt.show()
Вывод:
Теперь мы перевернем текущее изображение:
#Flip Down using scipy misc.face image flip_down = np.flipud(misc.face()) plt.imshow(flip_down) plt.show()
Вывод:
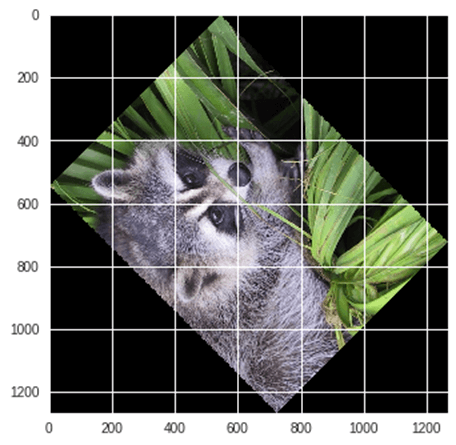
Пример : вращение изображения с использованием Scipy,
from scipy import ndimage, misc from matplotlib import pyplot as plt panda = misc.face() #rotatation function of scipy for image – image rotated 135 degree panda_rotate = ndimage.rotate(panda, 135) plt.imshow(panda_rotate) plt.show()
Вывод:
Интеграция со Scipy — Численная интеграция
- Когда мы интегрируем любую функцию, где аналитическое интегрирование невозможно, нам нужно обратиться к числовому интегрированию
- SciPy предоставляет функциональность для интеграции функций с числовой интеграцией.
- Библиотека scipy.integrate имеет правила одинарной, двойной, тройной, кратной, квадрата Гаусса, правила Ромберга, Трапеции и Симпсона.
Пример: теперь возьмем пример единой интеграции
Здесь а верхний предел и б нижний предел
from scipy import integrate # take f(x) function as f f = lambda x : x**2 #single integration with a = 0 & b = 1 integration = integrate.quad(f, 0 , 1) print(integration)
Вывод:
(0.33333333333333337, 3.700743415417189e-15)
Здесь функция возвращает два значения, в которых первое значение является интегрированием, а второе — оцененной ошибкой в интеграле.
Пример: теперь возьмем пример двойной интеграции. Мы находим двойное интегрирование следующего уравнения,
from scipy import integrate import numpy as np #import square root function from math lib from math import sqrt # set fuction f(x) f = lambda x, y : 64 *x*y # lower limit of second integral p = lambda x : 0 # upper limit of first integral q = lambda y : sqrt(1 - 2*y**2) # perform double integration integration = integrate.dblquad(f , 0 , 2/4, p, q) print(integration)
Вывод:
(3.0, 9.657432734515774e-14)
Вы видели, что выше вывод, как тот же предыдущий.
Резюме
- SciPy (произносится как «Sigh Pi») — это библиотека на основе Python с открытым исходным кодом, которая используется в математике, научных вычислениях, технике и технических вычислениях.
- SciPy содержит множество подпакетов, которые помогают решить наиболее распространенную проблему, связанную с научными вычислениями.
- SciPy построен на вершине NumPy
| Имя пакета | Описание |
|---|---|
| scipy.io |
|
| scipy.special |
|
| scipy.linalg |
|
| scipy.interpolate |
|
| scipy.optimize |
|
| scipy.stats |
|
| scipy.integrate |
|
| scipy.fftpack |
|
| scipy.signal |
|
| scipy.ndimage |
|